四象限变流器的空间矢量解耦控制

冷旭东

（深圳市泰昂能源科技股份有限公司，广东 深圳 518057）

与感应电机磁场定向的直接转矩控制相似，三相四象限变流器基于电压的解耦控制[1]和基于虚拟磁链定向的解耦控制[2]是通过直接对整流器输入输出功率进行控制，即通过估算功率和给定功率的偏差来实时确定开关状态的选择，以实现整流器直流侧和网侧能量的平衡。上述控制都是采用功率滞环控制器实现 PWM波形，开关周期的长度为功率误差ΔH从-ΔH到+ΔH然后再返回-ΔH变化一周的时间，实际控制中ΔH的变换频率是一个时变量，因此开关频率也不固定。开关频率不固定会使整流器运行噪声增加，而且产生的电磁干扰频带宽，EMI问题难解决。基于这种情况，本文介绍一种新的基于空间矢量的解耦控制，这种控制策略采用SVPWM 代替开关逻辑状态选择，因此可以解决开关频率不固定的问题。

1 虚磁链定向原则和整流器功率估算

根据park变换在静止坐标系上的三相正弦电压va、 vb、 vc，在空间上可以等效成为一按正弦角频率ω旋转的空间电压矢量vL，虚磁链矢量ψL是对vL的积分[2]，那么在空间上也是一按正弦角频率ω旋转的矢量。所谓虚磁链定向就是在αβ_dq坐标系中令虚磁链矢量ψL与d轴重合，即ψL=ψLd,ψLq=0，在αβ_dq坐标系中的各矢量关系如图2所示。

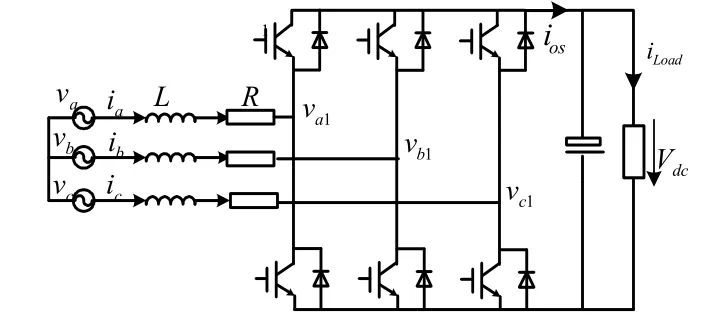
图1 三相Boost型四象限变流器主电路拓扑

图2 虚磁链参考坐标系和各矢量

运用复数定义，三相整流器瞬时有功功率p和瞬时无功功q率可以计算如下

式中，iL为整流器网侧电流合成矢量，为 iL的共轭。

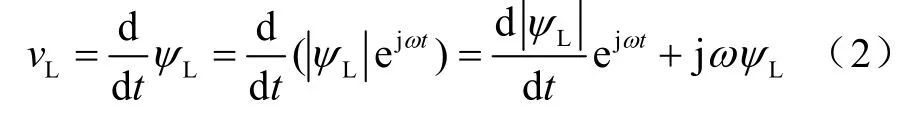
当三相电网电压平衡对称且为正弦，且整流器桥臂入端电压也平衡对称时则

式中，ψLα、 ψLβ为虚磁链矢量ψL的αβ轴分量。

式中，iLα、iLβ为整流器交流侧电流合成矢量的αβ轴分量。

则有

2 DPC-SVM控制原理及框图

借鉴国外三相电压型四象限变流器解耦控制研究现状[3-4]，DPC系统控制框图如图 3所示，与VF-DPC控制系统不同之处在于采用了 PWM空间矢量调制代替开关逻辑表。瞬时有功和无功功率估算值p和q与给定的 pref和 qref比较后输入 PI调节器，得到整流器入端电压dq轴电压vsd和vsq，再经转旋-静止坐标变换可得α-β坐标系参考电压vs的α-β分量vsα，vsβ，然后利用空间矢量调制可得到PWM开关信号对整流器中的开关器件进行控制。

图3 控制框图（DPC-SVM）

3 功率调节器参数的设计

由图1所示的虚磁链定向系统由于 ψL=ψLd，ψLq= 0 ，则

式中，vLd、vLq为三相正弦电压矢量的dq轴分量，Vm为三相正弦电压的幅值。

根据式（1）可以推知

将式（6）代入dq旋转坐标系下整流器的数学模型[5]可以得到

式中，L为整流器电抗器及线路的电感，R为整流器交流侧等效电阻，iLd、 iLq为网侧电流合成矢量的dq轴分量。

根据表达式（8）可以得到如图3所示的整流器简化数学模型。

图4 四象限变流器简化模型

为了零极点对消和设计方便，令

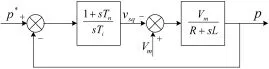
图5 有功功率调节器

式中，Tol是系统的开环时间常数，是一个很小的量。图4系统又可以简化为图5所示的一阶系统。

图6 等效有功功率调节器

闭环传递函数为

等式（13）说明无功功率的阶跃变量q0会对有功功率产生影响，因系统的闭环时间常数小于开环时间常数，式（13）可以简写为

类似的有功功率的阶跃变量 q0对无功功率的影响为

从式（14）和式（15）易知 Tcl的值取的越小，无功功率和有功功率间相互耦合影响也越小，实际运用中与系统采用时间常数保持一致。

则PI调节器参数为

由等式（11）推知，对于不同的 Tcl， kp/ki是一个常量且等于开环时间常数 Tol，Tcl除了对系统的快速性能有较大影响外，同时它的取值还决定着无功和有功功率环之间的解耦控制程度，因而是一个很重要的参数。

4 d、q轴耦合量相互影响分析

现对有功功率闭环进行分析，可将ϖLiLd看作扰动信号，令如图7所示。

图7 d、q耦合影响简化示意图

从图7可以分析出无功功率的变化对有功功率的影响，运用Laplace变换

再运用Laplace反变换

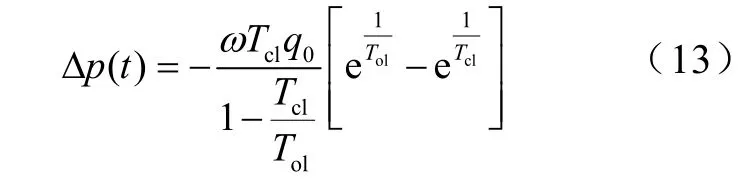
5 仿真结果分析

根据图2构建了三相电压型四象限变流器解耦控制系统基于Matlab/Simulink环境下的仿真模型，仿真主要验证在三相不平衡时的稳态运行波形。仿真主电路参数为相电压幅值 Vm= 2 50V ，等值电阻为 R = 0 .1Ω，电感为 L = 1 0mH ，直流侧电容为 C = 1 mF，负载 R = 5 0Ω。直流电压给定 Vdc*= 6 00V ，采样频率为 fN= 1 0kHz，平均开关频率为 f = 4 kHz。则功率调节器参数为Tcl= 1 0-4s ， kp= 0 .4， ki= 4 。三相不平衡电压定义为

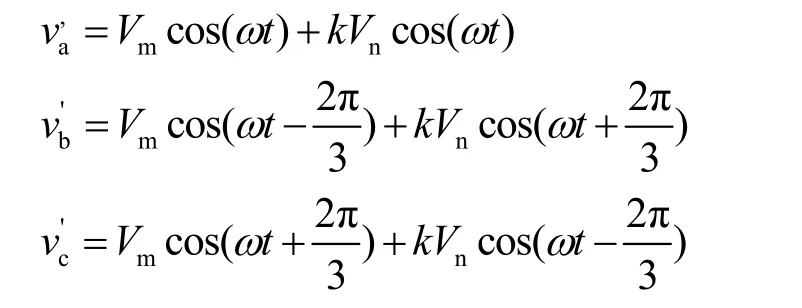
Vn= 3 00V， k = 0 .05时整流器输入a相线电流波形及谐波频谱见图 8，可以看出当电源电压三相不平衡时，系统网侧电流THD为4.12%。

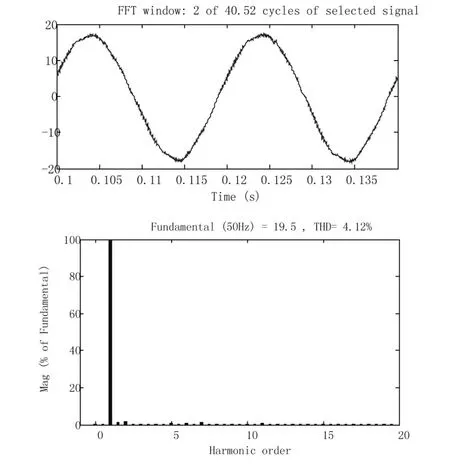
图8 DPC-SVM系统三相不平衡时网侧a相电流波形及THD

从仿真结果可以看出在电源电压三相不平衡情况下， DPC-SVM系统网侧电流 THD很小，从而显示出这种控制策略的最大优点。

6 结论

从四象限变流器的模型上看，控制难度最大的变流器三相之间的耦合，采用PARK变换并以旋转坐标系作为研究基础后，三相间的耦合演变为两轴之间的耦合，采用虚拟磁链的分析方法，将 dq两轴动态解耦，能使有功电流、无功电流分别控制，达到精确控制的效果。仿真结果证实了以上设想。

[1]T.Noguchi,H.Tomiki,S.kondo,and I.Takahashi.Direct power contrl of PWM converter without power source voltage sensors.IEEE Trans.Ind. Appl.,1998,34(3):473-479.

[2]M.Malinowski and M.P.Kazmierkowski“virtual Flux Based Direct power control of three phase PWM rectifier.IEEE Trans.Ind.Appl,2001,37(4):1019-1027.

[3]M.Malinowski,M.P.Kazmierkowsk Simple Direct Power control of three phase Pwm rectifier.Using space-vector Modulation IEEE Trans.Ind.Appl, 2004,51(2):447-454.

[4]Ambrozic V,Fiser R,Nedeljkovic D.Direct current control-a new current regulationg principle [J]. IEEE Trans. power Electron.,2003, 18(1): 495-503.

[5]张崇巍.张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.10.