三相四线制光伏并网发电与电能质量调节器的统一控制

文 文

（南方电网超高压输电公司贵阳局，贵阳 550000）

随着传统化石能源的不断衰竭，新能源发电技术呈现出越来越快的发展趋势。而这些新能源中将会有较大一部分以分布式发电形式接入在电网中，这些通过并网逆变器并入低压电网的分布式发电系统将会对低压配电网的运行与管理产生较大的负面影响。然而，在另一方面，如果能将这些并网逆变器功能与电能质量调节器的功能相结合，实现在向电网注入用功电能的同时，还能对电网的电能质量进行调节，将会取得较大的收益。

并网逆变器可以分为电压型并网逆变器[1]和电流型并网逆变器[2]，对于电压型并网逆变器，其与电网并联运行的输出控制可分为电压控制[3]和电流控制[4]。并网输出采用电压控制时，实际上就是一个电压源与电压源并联运行的系统，这种情况下必须要保证逆变器输出电压与电网电压同幅、同频、同相，其控制较为复杂，尤其是在配电网中，电网电压经常会有较大的畸变，很难达到预期效果。而如果逆变器的输出采用电流控制，则只需要控制逆变器的输出电流以跟踪电网电压，同时设定输出电流的大小，即可达到并联运行的目的。由于其控制方法相对简单，效果也比较好，因此使用广泛。并且采用电流控制时，还可以控制逆变器在输出正弦有功电能的同时，向电网注入相应的无功和谐波电流，用以改善电网的电能质量。

目前，已有不少文章对并网发电和电能质量调节的统一控制进行了研究。然而，这些研究大多是针对三相三线制系统[5-7]或单相系统[8]，对于三相四线制并网系统的研究却很少。在三相四线制系统中，除了由谐波和无功产生的电能质量问题外，还有不平衡电流产生的电能质量问题。不平衡电流会导致三相电压不对称、线路以及变压器损耗增大，甚至在不平衡度过大时，导致中线电流过大而烧毁中线[9]，从而威胁到电气设备的正常运行。基于此，本文以目前研究较多的新能源之一——太阳能为研究对象，设计了一种三相四线制光伏并网发电系统，该系统输出采用电流控制。在并网运行时，除了向电网输出正弦有功电流外，还可以对电网的无功和不平衡电流进行补偿，并且对谐波具有一定的抑制作用，从而达到改善电能质量的目的。并且该系统在夜间光伏电池不能发电的状态下，继续以有源滤波器的状态工作，有效提高了并网逆变器的利用率。

1 光伏并网系统的基本结构及其工作原理

光伏并网的基本结构如图1所示，系统主要由光伏电池板、一个 DC/DC（Boost）变换器以及一个DC/AC变换器（逆变器）构成。其中Boost变换器负责将太阳能电池组件的宽范围直流输出电压变换为并网逆变器所需要的稳定的直流母线电压，并实现最大功率点跟踪（maximum power point tracking，MPPT）；三相四线制的并网逆变器，负责将光伏电池发出的电能以交流电的形式送入电网，供负载使用。

图1 光伏并网系统的基本结构

1.1 光伏电池的仿真模型

图2是光伏电池等效模型[10]。它由理想电流源Isc，反向并联二极管D、串联电阻 Rsh和并联电阻 Rs构成。其中 Isc的值等于电池的短路电流，其大小反映了光伏电池所处环境的日照强度。日照越强， Isc越大；反之越小。式（1）是光伏电池的I-V特性关系方程。

式中， Tc是电池内部绝对温度，V是光伏电池输出电压， Id0是二极管饱和电流， Rsh是内部并联电阻，Rs是内部串联电阻，q是电子电荷，为1.602×10-19C，A是二极管系数,通常为1.0～3.0，k是波尔兹曼常数，k=1.38058×10-23J，n是多个电池串联系数。

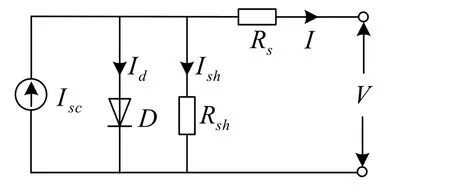
图2 光伏电池的等效电路

图3是根据上述仿真模型在PSIM6.0中搭建起仿真电路得到的光伏电池的I-V和P-V曲线，可见该仿真模型可以较好的反应光伏电池的特性。

图3 光伏电池的I-V、P-V特性曲线

1.2 并网逆变器拓扑的选择

三相四线制并网逆变器的拓扑类似于三相四线制有源电力滤波器[11]，主要有三种典型的拓扑结构，即电容器中分式、四桥臂式以及三单相全桥式[12]。已经有不少文章对这三种拓扑的特点进行比较[13]，电容器中分式结构由于中线电流完全流入电容，且两个电容电压之间不均衡，需要额外的均压控制，所以这种补偿能力有限，适用于中线电流较小的场合；四桥臂式结构单独利用一个桥臂对中线电流进行控制，控制效果以及对中线电流的补偿能力均要优于前者，其主要的控制难点在于中线桥臂开关状态的选择；三单相全桥式结构由于各相完全解耦，控制最为灵活和简单，并且补偿功率大，虽然完全从技术角度上考虑是最优选择，但是由于需要隔离变压器进行并网以及开关器件个数众多，成本过高。本文的设计采用四桥臂式结构作为逆变器主电路，其结构如图4所示。

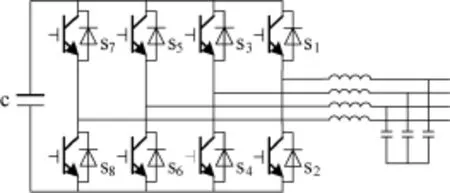
图4 四桥臂逆变器主电路

2 光伏并网发电与有源滤波的统一控制

控制系统的结构如图5所示，光伏电池以直流源的形式，为并网逆变器提供电能，并网逆变器采用电流控制方式，以电流源方式向电网注入功率，传统的方式是将输出电流控制为与电网电压同频同相的正弦波，以达到向电网注入有功功率的目的。由于常规并网逆变电源直流母线电压控制与有源滤波器的直流母线电压的电压控制方式是一致的，即通过调节并网电流有功电流分量的大小和方向来稳定直流母线电压[14]，并且它们的输出都是采用的电流跟踪控制。因此，两者的统一控制是可行的，通过检测负载交流母线上的无功、谐波以及不平衡电流分量，并将其换算为补偿电流指令，与逆变器所要输出的有功电流指令相合成，即可得到最终并网电流指令，经电流内环调节即可实现光伏并网发电和电能质量调节的统一控制。

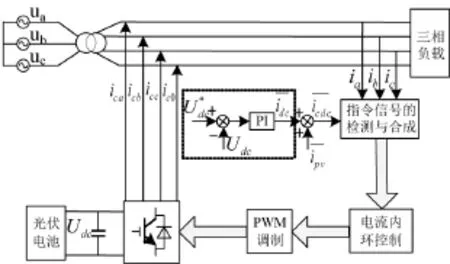
图5 光伏并网发电与有源滤波的统一控制

并网逆变器采用电压控制为外环、电流控制为内环的双环控制结构。电压外环稳定直流侧电容电压，如图中虚线框内所示部分，利用直流侧实际的检测电压 Udc与直流侧参考电压的误差经过 PI调节后的输出来调节电流内环的线电流参考给定幅值信号，用以抑止直流侧电压的波动；为逆变器所要输出的并网有功电流的幅值，它是与MPPT环节中所计算出的每一时刻的最大功率相对应的，用以保证光伏电池发出的功率与并网逆变器的输出功率相等，实现系统的功率平衡。电流内环实现并网电流的跟踪控制，并保证电流跟踪的快速性以及较小的误差。

要实现对电能质量调节以及并网电流的综合控制，其关键技术是电网无功、谐波以及不平衡电流的检测，并将检测的指令信号与并网电流指令信号合成。为了保证电网的供电质量，系统必须能够实现对无功电流补偿的快速反应。在电流检测完成的基础上，其各相检测值作为补偿电流的指令值，与直流电压环输出并网电流的有功分量合成，作为调节器输出电流指令。

3 指令信号的检测与控制

对于三相四线制系统的谐波、无功以及不平衡电流的检测，目前采用较多的是基于瞬时无功功率的检测方法[15]，以ip-iq法为代表的瞬时无功功率理论的突出优点是实现电路比较简单、延迟少,且具有很好的实时性。其原理框图如图6所示。

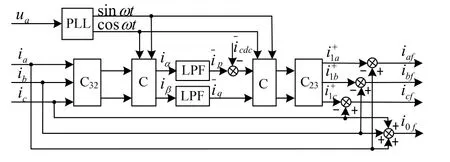
图6 基于瞬时无功功率的谐波及无功电流检测

设三相三线制系统三相不平衡电流 ia、ib、ic为

将它们经过C32和C矩阵变换并通过低通滤波器滤波后可以得到

传统的做法是将式（4）进行Park反变换和C23变换（如图6所示）得到三相基波正序电流，即

式中，CT、C23分别为C、C32的逆矩阵。

然后将实际电流 ia、ib、ic分别与上面得到的三相基波正序电流相减，即可获得实际电流中的谐波分量及应补偿的不平衡分量，将上述得到的量作为参考值与逆变器实际输出的进行比较，形成闭环控制；如果系统需要同时检测无功分量，则只需将基波有功直流分量I1p经CT和C23的逆变换，进而获得实际电流中的基波有功电流分量，将实际电流 ia、ib、 ic与其基波正序电流的有功分量相减，即可获得其中的基波无功、谐波分量以及不平衡补偿分量。

然而由于该逆变器的功能设计中要求具有对电网中的不对称电流进行补偿的功能，因此，逆变器实际输出的电流将不再是对称的，即有可能同时含有正序、负序以及零序分量，采用传统的控制方法难以同时实现对这三个分量进行较好的控制，导致实际的输出电流存在较大的误差。基于此，本文提出了针对三相四桥臂逆变器输出电流的解耦控制策略，其控制原理如图7所示。

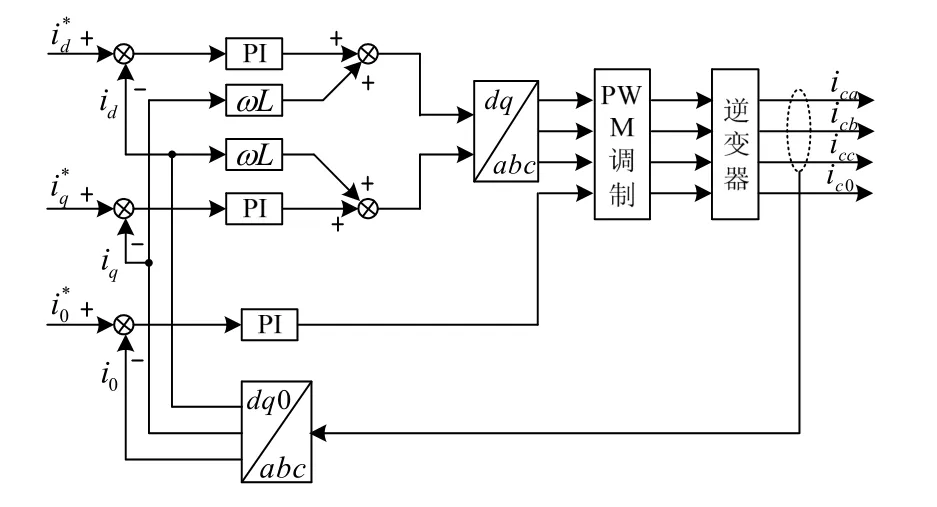
图7 三相四桥臂逆变器输出电流的解耦控制

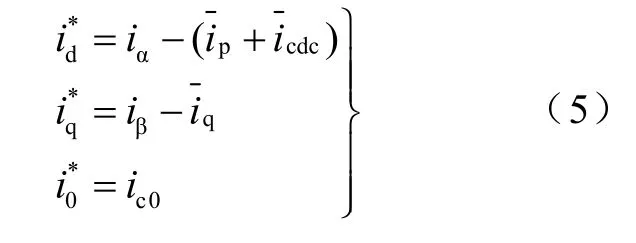
图中d、q通道的前馈项Lω id与Lω iq的作用是实现d轴和q轴电感电流的完全解耦。abc/dq0坐标变换与图6中的CC32矩阵变换基本等效，不同的只是abc/dq0坐标变换中多了一个零序分量分离通道，而这一通道在图 6中已单独给出；dq/abc坐标变换与图 6中的 CTC23矩阵变换完全等效，二者的表达式如下所示：

4 逆变器工作模式的切换

本文所设计的光伏并网发电系统具有白天并网发电、夜晚不停机继续工作在有源滤波器状态的两种工作模式。这两种工作模式的切换通过检测图6中的大小来实现的，如上所述大小反映了光伏电池所发出功率的大小，当检测到小到一定值时，说明此时的光伏电池板已经基本不发电了，可以将其切除，并将的值设为0，则此时并网逆变器成功的实现了工作模式的切换，仅工作在有源滤波器的状态。

5 仿真研究及结果

根据上述对光伏并网系统所实现的功能的要求，即在实现注入有功电能的同时还可对电网的谐波、无功以及不平衡性电流进行补偿，运用PSIM6.0仿真软件对该系统在三种不同的工作状态下进行仿真，即只进行电能质量调节、同时进行电能质量调节并网发电以及光伏电池输出功率突变。仿真时设置电网线电压为380V、频率50Hz，三相负载为非对称性负载，且a相负载为非线性负载，图8为逆变器未投入运行时三相电网的电流以及中线电流，从图中可以看出三相电流存在较大的不平衡性，且中线电流较大。

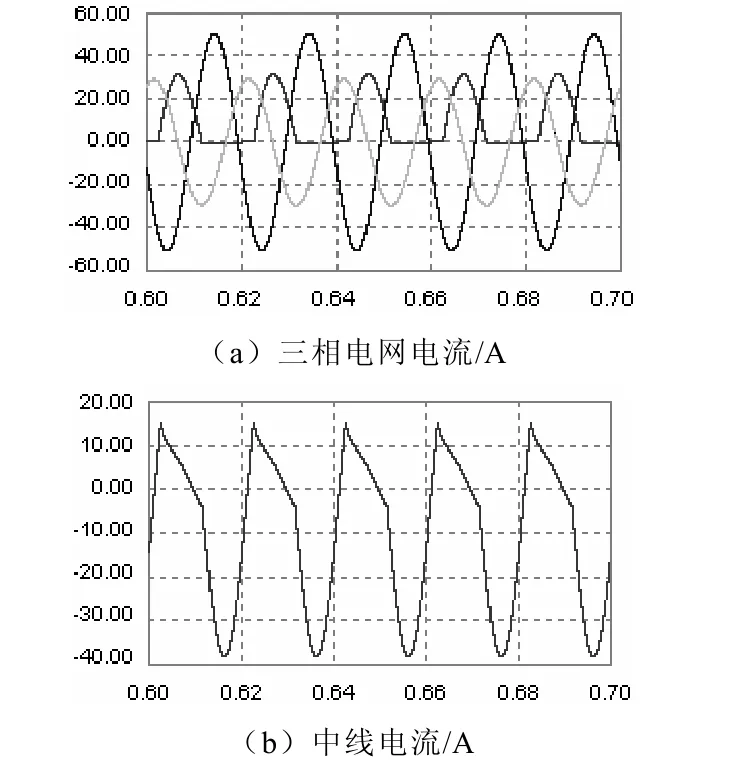
图8 逆变器未投入运行时电网电流（t/s）

图9为逆变器仅工作电能质量调节状态下在电网电流，此时的逆变器相当于一个三相四线制有源电力滤波器，起到改善电网电能质量的作用，从图中可以看出，逆变器投运以后，电网电能质量得到了极大的改善。

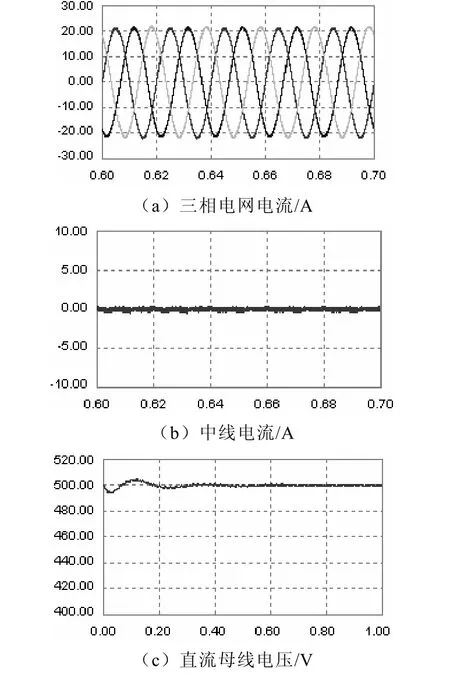
图9 逆变器工作于电能质量调节器时的波形（t/s）

图10为逆变器同时工作在电能质量调节和并网发电时的波形，此时的逆变器在对电网提供谐波、无功以和不平衡性电流补偿的同时，还向电网注入一定的有功电能，从图中可以看出三相电流为与三相电压波形相同的纯正弦波形，且由于有功电流的注入，电网电流减小；从c图中可以看出直流母线电压是稳定的，表明系统工作是稳定的。

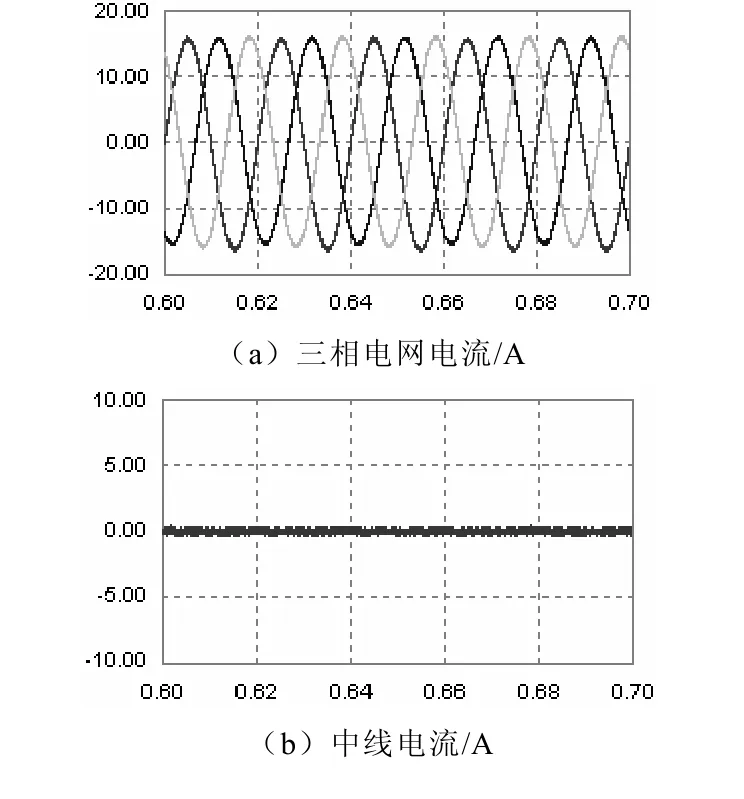
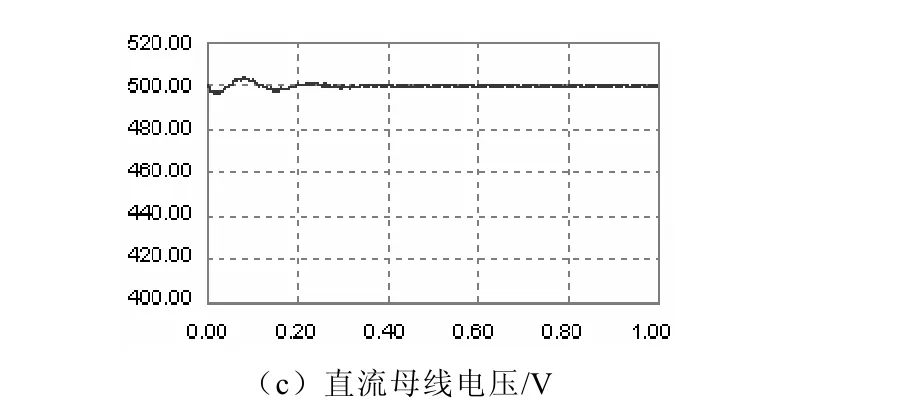
图10 逆变器同时工作于并网和电能质量调解时的波形（t/s）

图11为系统中光伏电池输出功率突变的情况下系统的工作波形，此时的的负载电流仍然如图 8所示，在0.65s出，光伏电池输出功率突然减小如a所示；由于光伏电池输出功率的减小，导致其并网电流减小，从而导致电网向负载提供的电流增大，如图b所示；图c为光伏电池输出功率突然减小的情况下的直流母线电压，可以看出其仍然是比较稳定的，也就是说该系统在动态情况下具有较好的稳定性。

图11 光伏电池输出功率突变情况下的波形（t/s）

6 结论

本文为分布式发电系统设计了一种三相四线制光伏并网发电系统，该系统中并网逆变器将有源滤波器和并网发电控制相结合，在实现并网发电的同时，还可以对电网的谐波、无功和不平衡电流进行补偿，从而改善电网的电能质量，为配电网电能质量的改善提供了一条新的途径，并且对于进一步提高三相四线制并网逆变器的灵活性和应用范围具有较大的意义。仿真结果验证了该设计的有效性和可行性。

[1]吴浩伟,段善旭,徐正喜.一种新颖的电压控制型逆变器并网控制方案[J].中国电机工程学报. 2008,28(33):19-24.

[2]吴春华,崔开涌,陈国呈,陈卫民,肖鹏,张翼.一种电流型并网逆变器的拓扑和控制方法[J].电工技术学报.2007,22(08):7-12.

[3]LEE S W, DEHBONEI H, KO S H, LEE S R. Power electronics and drive systems[C].PEDS’07.7th International Conference. 2007:1508-1512.

[4]ABEYASEKERA T, JOHNSON C M, ATKINSON D J.Suppression of line voltage related distortion in current controlled grid connected inverters[J]. IEEE Transactions on power electronics. 2005, 20(6):1393-1401.

[5]王正仕,陈辉明.具有无功和谐波补偿功能的并网逆变器设计[J].电力系统自动化. 2007,31(13):67-71.

[6]张国荣,张铁良,丁明,苏建徽,汪海宁. 光伏并网发电与有源电力滤波器的统一控制[J]. 电力系统自动化.2007,31(08):61-66.

[7]HAN B,BAE B,KIM H. Combined operation of unified power-quality conditioner with distributed generation[J].IEEE Transactions on power delivery. 2006, 330-338.

[8]张强,刘建政,李国杰. 单相光伏并网逆变器瞬时电流检测与补偿控制[J]. 电力系统自动化.2007,31(10):50-54.

[9]林志雄,陈岩,蔡金锭,李天友. 低压配电网三相不平衡运行的影响及治理措施[J].电力科学与技术学报,2009,24(03):63-67.

[10]任碧莹,钟彦儒,孙向东,同向前. 基于PSIM软件的光伏电池特性的仿真建模研究[J].西安理工大学学报,2007,23(04):257-260.

[11]LAMICH M, BALCELLS J, GONZALEZ D. Control to reduce leading current in a Shunt Hybrid Power Filter[C]. 6th International Conference and Workshop on Compatibility and Power Electronics. 2009, 73-78.

[12]陈仲.并联有源电力滤波器实用关键技术的研究[D].杭州: 浙江大学,2005.

[13]SINGH B, AI-HADDAD K, CHANDRA A. A review of active filters for Power quality improvement[J].Industrial Electronics, IEEE Transactions on. 1995,46(5):960-971.

[14]ZARGARI N R, JOOS G. Performance investigation of a current-controlled voltage-regulated PWM rectifier in rotating and stationary frames[J]. IEEE Trans Industrial Electonics, 1995, 42(4):396-401.

[15]AKAGI H, KANAZAWA Y, NABAE A. Generalized theory of the instantaneous reactive power in three-phase circuits.In：IEEE&JIEE. Proceedings IPEC.Tokyo: IEEE, 1983: 1375-38.