大容量风电场中风速造成的并网问题研究

肖硕霜 尹忠东

（华北电力大学新能源电力系统国家重点实验室，北京 102206）

相较于其他形式的能源，风电以其清洁、高效、可再生性与低廉的建设成本赢得了各国政府与市场的广泛关注。风电场规模的不断扩大也带来了不可避免的并网问题。随着风电热的不断升温，风电场逐渐表现出发电场容量增大、并入电网的等级增加的特点，单个风电场装机容量攀升至百万千瓦，并由配网接入发展为直接接入高压电网。可以看到，增加的容量和接入电压等级将使得风电对所并入的电网影响更加深远。

风电机组的输出功率受不可控的随机自然风力驱动会频频波动。由于风电资源丰富的地方往往在电力系统薄弱的偏远地区和沿海，其单一的网络结构和薄弱的电气联系又使得其输出功率一旦受到波动则会造成电网局部的电能质量显著改变，稳定性也受到干扰。在风电穿透率较低时，风电场的间歇性与波动性系统都可以耐受。超过8%的风电穿透水平，便需要切除机组舍弃部分风电。现代风电占电网比例迅速上升，这样一来舍弃风电量将相当可观。为尽量避免弃风的经济损失，保障大容量风电场并网的安全运行，研究风速波动的对其造成的并网影响迫在眉睫。

1 大容量风电场风速波动下的影响

经过各国对风电场并网问题的研究探索，风速的波动主要体现在风机机械转矩改变造成的电磁转矩的非额定运行。此间发电机有功输出波动，电能质量改变乃至影响到整个风电系统的并网潮流亦会随之改变。

1.1 风速波动的并网电压影响

风速波动产生的有功输出波动从根本上引起了并网点电压的波动与闪变，其中电压波动也是 IEC标准对并网风电考察的重点。其余的原因还有电网状态、机组类型、机组控制等原因，并不赘述。

在高渗透率的电网中，主流的恒频恒速风电机组直接与电网耦合，风电产生功率特性将直接体现在电网中。另外，其异步发电机在输出波动有功时将会吸收大量的无功。风速的变动直接影响到无功吸收的大小，无功吸收减少导致并网点电压降低，而风机侧固定电容器补偿的无功容量则与电压相关，从而导致了电压的进一步恶化。如若任由发展，降低的电磁转矩造成转矩不平衡，轴系松弛功率无法送出，异步发电机将会转速飞升，甚至可能引起母线电压崩溃造成电量损失与失稳。

图1 单相风电机组输出电压虚拟电网模拟

而显然式中风电机组有功如下

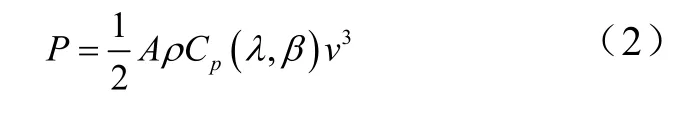
设最初风速23m/s，当出现持续6s、以±6m/s速率逐渐变化的典型阵风时，十万千瓦装机容量风电场出口母线电压变化幅度为-5%～4%。研究表明，风电机组端电压的波动与闪变随平均风速的增加而增加。风速超过额定值又继续增加时，变转速机组由于具有可平滑有功波动使得电压波动减小，恒转速机组的波动仍旧增大。湍流强度与电压波动与闪变的关系几乎可表示为正斜率特性。

为评估并网运行的电压波动，可考虑风速服从瑞利分布并依据 IEC标准中的闪变值算法进行估算。考虑大型风电场有多台风机，则引起的短时与长时间闪变值为[1]

式中， ci（ φk, va）s是每台机组闪变系数，是由闪变系数在瑞利风速下的积累概率函数计算得出的。

式（3）中，N为并网点连接风电机组数； Sn,i为每台机组额定视在功率； Sk为机组公共并网点短路容量； Sks为虚拟电网短路容量； Pst是根据风机输出电压按照IEC标准计算得出的短时闪变值。

1.2 风速波动的并网频率影响

现代风力发电系统中越来越多地采取了变速风电机组或者安装有电力电子变流器的恒速风电机组，这样的机组虽然控制性能大大进步，但同时使得机组机械和电气联系解耦，阻断了转子转速与电网频率变化的响应关系。单纯的恒频机组采用恒转差运行，能够维持恒定功率水平。因此，当电网频率改变时，风力发电机组输出功率仅与风能有关，不能对系统频率变化产生响应。

综合目前对风速统计分析得出，单台风电机组输出的波动功率水平主要为秒级，但量值很小；风电场由于集群效应其波动则更为平缓，秒级的风速变化率不大，99.44%的情况下变化率都小于0.3%；而分钟级以上的功率波动则会对电网的频率带来一定的影响。另考虑风电的集群平滑作用，当风电场群入网后，出现大于70%全网风电容量的功率波动概率将极低。但若渗透率较高，将会在全网造成系统有功出力和负荷之间的动态不平衡，对电网频率造成很大打击。我国电力系统的频率偏差标准为50±0.2Hz，这是风电引起的频率波动必须控制的范围。

在我国风电场并网导则中规定风电是不需要参与调频的。这是由于风电功率无法控制，做备用的可靠性极低。电网的调频重任必须由传统水火电厂承担。

对于数分钟至小时级功率波动的二次调频，在其他国家的风电导则中，提出了风电在系统频率受到影响时需要限制风电出力来参与二次调频。如爱尔兰则要求风电场需要将 3%～5%的出力进行控制来参加系统调频、丹麦规定风电场需要采用弃风方式来留出一定的调频容量。我国电网导则没有提出相关要求。二次调频是手动或自动根据事先的预测值控制风电机组发出功率的增减。预测值由风电出力预测和电网调度预测（仍考虑负荷预测）综合考虑得出的，如果风电的功率波动超出了预测值，备用无法响应时则也会造成系统的功率不平衡和频率变化。这就需要电网增加更多的调频电源容量来应对。

研究表明，穿透功率愈大，风电场并网所需的额外备用就愈多。当风电的穿透水平达到10%时，功率波动的影响才会明显地体现在二次调频备用容量上来，而额外增加的备用意味着额外增加的成本，这可能造成传统电力机组的频繁启停或未满载运行造成效率低下、风电机组参与的机组最优组合复杂化，从而引起调频负担加重、调度困难与运行成本增加。

据以上分析可粗略估算并网风电的容量。风电出力变化率为一定时，风电接入率增大，则所要求的系统调频速度越大。依张家口风电场数据分析[9]，设若当调频速度为每分钟1.2%时，则必须要求风电接入率限制在40%以下。

1.3 风速波动对电网潮流影响

给定风速，风电场的有功功率特性可以表示为如下

式中，A、B、C为功率特性系数，V为风速， Vci、Vco、Vr分别代表风机启动风速切除风速以及额定风速， Pr为额定风电出力。

传统潮流计算中，电网的母线可以划分为 PQ节点、PV节点和平衡节点三类。对于变速风力机组，无功可以根据控制策略的设定或者功率因数求取。而恒速风电机组则不同，其自身无法进行励磁调节不能调节电压免受偏移；其所吸取的无功，又与发出有功、电压、滑差有关，不能保证功率恒定。所以是不能单纯将风电场母线划分为某一类节点的。

采用风电场潮流联合迭代模型[27]，简化异步发电机的等值电路，如图2所示。由等值电路可以得到注入电网的有功和无功分别为

由上式可知无功可以辨识为有功和电压的函数。改进雅克比矩阵并采用牛顿-拉夫逊法，可以得到风电场并网系统的潮流。

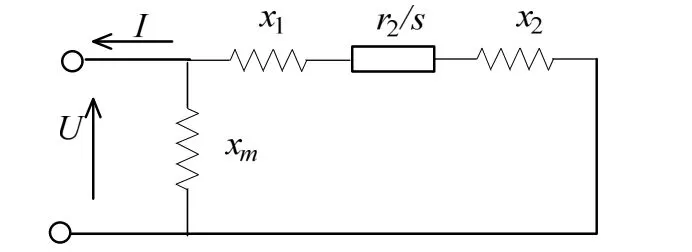
图2 简化异步发电机等值电路

动态系统下中，如果采用了传统稳态潮流计算方法，风速变动强烈的情况下，计算结果将会产生一定的误差。可以采用蒙特卡罗法计算概率潮流，将电力系统中负荷、风电机组出力等概率分布进行抽样，再进行稳态潮流计算，得到与抽样值对应的潮流计算结果后进行分析得到系统潮流的概率分布。

另外，潮流结果也与并网点连接风电场之间的风速相关性密切相关。文献[25]研究改进的IEEE30节点系统发现：当风速相关性高时至少需要22.5Mvar无功补偿量来保证各节点电压不越限，而设风速无相关性则仅需6Mvar的补偿量；考虑相关性时的风电场的最大装机容量比不考虑时超过了34MW，若按后者装机容量进行系统规划，则必定会使系统中部分节点电压越限的概率大于5%。实际工程中需要考虑这一点。

2 风速波动对电网影响的解决措施

就目前而言，解决风速波动造成的大规模风电并网问题主要还处于理论研究，因为世界范围内具有高极限穿越功率的国家相当有限，北欧国家风电发电量仅占电力系统的 1%～2%，美国与我国则更低。但随着风电快速发展，解决此问题是不可避免的。而以上对风速波动造成的并网影响问题的解决方式是相辅相成的，其最根本的就是将风电机组输出的有功功率进行平滑。

尽量准确预测风速可以相应提高风电功率输出的预测准确性，从而显著降低所需调频备用。通过合理有效的统筹管理、较准确地进行风速和功率的调节和控制是发电调度计划制定的重要参考，从而及时提供备用、减少电压和频率波动可能性。目前预测方法主要有随机时间序列法、人工神经网络法、卡尔曼滤波法等。当渗透率为10%时，约需要额外的调频备用为2%～8%的风电装机容量。如果采用先进预测技术及当日甚至小时前调度，则只需2%～4%的装机容量。

由上文分析，备用容量增加意味着经济和电网调度的困难。寻找新的平衡方式如功率补偿器也是现在的热点。现广泛采用的是安装无功补偿器如SVC、STATCOM 来提供一定无功稳定风电场出口电压。在频率方面，有研究将风电场看作负的负荷，来通过AGC（自动发电控制系统）调节系统发出的有功较好的解决其随机性的问题[26]。但是其综合效果却没有新兴的储能装置优越，当然后者的成本是重要的制约因素。储能装置对有功无功都可以进行有效补偿，其提供的有功有效弥补机组有功输出波动、缓解电压频率偏差，弥补纯无功补偿的不足。

采用飞轮储能、超导储能、蓄电池储能等在一定程度上能够平滑风电的有功波动。分析风电输出功率频率知，大部分都处于低频域，0.01～1Hz频段对电网影响最大。现在的研究往往采用高通滤波器得到电池储能系统的参考输出[19-20]，即式中， Pw为风速。

电池储能系统的容量可由该功率在时间上的积分求取，而根据截止频率 0.01Hz求得时间常数τ= 1 5.9。研究表明，既可以有效平抑风电场功率波动，又可以提升风电场的整体备用容量。

另外，由于连接点的短路比与电压波动呈负增长关系，所以优化电网结构、增加风电场与电网间的电气联系、增大风电场并网点短路容量也将有效减小风速改变引起的电压波动。

3 结论

通过前文分析，自然不可控风速对风电场接入系统造成的影响在渗透率（以发电量计）较低时可以由电力系统的自动调节装置进行缓解，但能力与效果有限。当渗透率较高时，随机波动的风电出力对电网电压和频率、潮流等的影响很可能越限，会造成电网不稳定甚至解列、崩溃的后果，加重了发电调度负担，大大增加了经济成本。因此，风速造成的功率波动对大规模风电并网的进一步研究刻不容缓。

[1]孙涛,王伟胜,戴慧珠,杨以涵.风力发电引起的电压波动和闪变[J].电网技术,2003,27(12):63-69

[2]田继伟,张新燕. 风电场并网引起的电压波动仿真[J].电机技术,2008.5:5-7.

[3]张震,曹增杰.试论风电系统中的电压波动及抑制措施[J].科技情报开发与经济,2001,21(20):147-149.

[4]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J]. 中国电机工程学报,2005,25(11):1-5.

[5]张占奎.超导磁储能系统在并网风电场的应用研究[D].西安理工大学,2010.

[6]蒋大伟.大规模风电并网对系统频率影响分析[D].东北电力大学,2010.

[7]邓美玉,杨祉涵,戴朝华.风电并网建模及其渗透率对电网稳定性的影响[J].电力学报,2011,26(4):282-286.

[8]张丽英,叶廷路,辛耀中,韩丰,范高锋. 大规模风电接入电网的相关问题及措施[J].中国电机工程学报,2010,30(25):1-9.

[9]韩小琪,宋璇坤,李冰寒,戚庆茹. 风电出力变化对系统调频的影响[J].中国电力,2010,43(6):26-29.

[10]蒋佳良,晁勤,陈建伟,常喜强.不同风电机组的频率响应特性仿真分析[J].可再生能源,2010,28(3):24-28.

[11]计崔.大型风力发电场并网接入运行问题综述[J].华东电力,2008,36(10):71-73.

[12]袁越,李强,李群,张新松.风电功率特性分析及其不确定性解决方案[J].电力科学与技术学报,2011,26(1):67-72.

[13]宇航.利用储能系统平抑风电功率波动的仿真研究[D].东北电力大学,2010.

[14]DANY G. Power reserve in interconnected systems with high wind power production[C]. IEEE 2001 Porto Power Tech Conference, 10-13 September 2001,Porto.

[15]吴淳.风电对电力系统调频和备用的影响研究[J].华东电力,2011,39(6):993-997.

[16]韩民晓,崔军立,姚蜀军,Lie XU.大量风电引入电网时的频率控制特性[J].电力系统自动化,2008,32(1):29-33.

[17]侯佑华,房大中,齐军,李洪波,牛伟,杨涛.大规模风电入网的有功功率波动特性分析及发电计划仿真[J].电网技术,2010,34(5):60-66.

[18]倪琳娜,罗吉,王少荣.含风电电力系统的频率控制[J].电工技术学报,2011,26(增1):235-241.

[19]李国杰,唐志伟,聂宏展,谭靖.钒液流储能电池建模及其平抑风电波动研究[J]. 电力系统保护与控制,2011,38(22):115-125.

[20]毕大强,葛宝明,王文亮,柴建云.基于钒电池储能系统的风电场并网功率控制[J].电力系统自动化,2010,34(13):72-78.

[21]张坤,毛承雄,陆继明,王丹,黄辉.基于储能的直驱风力发电系统的功率控制[J].电工技术学报,2011,26(7):7-14,43.

[22]范高峰,于德龙,任普春,陶程,戴慧珠.变动风速作用下风电场对电网电压的影响分析[J].电网技术,2006,30(增):230-233.

[23]刘忠仁,刘觉民,邹贤求,吕立召,祖映翔. 电池系统对风电并网引起的频率波动控制应用[J].电力系统及其自动化学报,2011,23(6):62-66.

[24]刘梦欣,王杰,陈陈.电力系统频率控制理论与发展[J].电工技术学报,2007,22(11):135-145.

[25]范荣奇,陈金富,殷献忠,李慧杰,姚美齐.风速相关性对概率潮流计算的影响分析[J].电力系统自动化,2011,35(4):18-22.

[26]贾涛.大规模风电场并网后AGC平抑频率波动研究[D].山东大学,2009.

[27]王海超.风力发电并网问题研究[D].清华大学,2006.