配电网中光伏微网系统的新型控制策略
夏向阳 万 成
(长沙理工大学电气与信息工程学院,长沙 410114)
随着全球经济的飞速发展以及石化能源的过度消耗,环境及能源问题已经变得十分严峻。具有清洁、可持续使用的太阳能被公认为是当今国内外最具发展潜力的新能源[1-2]。随着人们对环境保护与节能减排的日益关注,光伏微网系统的大规模生产和投入使用已经成为一种趋势。
与传统的发电方式相比,太阳能光伏发电具有清洁干净、时间长久、获取方便、数量巨大等优点[3]。目前,国内各大太阳能光伏发电设备生产厂家,如无锡尚德、常州天合、中电电气(南京)、北京清华阳光能源随之也相继宣布太阳能光伏微网系统研究计划。根据研究预计,2020年光伏发电量将占全球总发电量的1%左右,到2040年约占20%[4]。可见,光伏微网系统正在迅速进入电力能源结构,并且将逐步成为其不可或缺的一部分[5]。然而,随着光伏发电大量进入系统,将对电网的稳定运行产生影响。传统的无源滤波器已经不能满足现在电力对电能质量的要求,因此,光伏并网装置和有源滤波器(APF)相结合的复合控制成为近年来国内外研究的热点[6]。
目前已有研究成果中,光伏并网运行时,并网瞬间整流装置会对电网产生冲击电流,运行时由于天气原因使直流侧电压不稳定,产生电压闪变,影响电网的安全运行,文献[7]提出了对负载不稳定电流的抑制,却没有提出详细的解决方案;文献[8]基于有源电力滤波器,提出了用于直流侧电压控制的模糊PI控制方法,稳定性强,滤除谐波效果良好,但是响应速度缓慢,且没有详细分析有源电力滤波器滤波的控制策略。文献[9]基于瞬时无功功率理论,提出了无功及谐波电流的检测方法,但是没有解决系统稳定性问题。文献[10]给出了无功补偿和光伏并网发电的统一控制方法,但是并没有考虑负载侧电流的不稳定因素,也没有充分利用两者的优点进行进一步的功能拓展。
基于此,本文综合分析了应对滤除各次谐波的稳定复合控制策略。首先基于LCL型三相光伏微网系统的结构,分析了其工作原理,建立了滤波器的数学模型;然后,基于滤波器的数学模型,提出一种PI控制与无差拍控制相结合的复合控制策略。通过仿真证明:本论文提出的控制方案能有效提高光伏发电率,改善电网的电能质量,对确保电网的安全经济运行有一定的作用。
1 组合系统结构及模型
1.1 主电路拓扑结构
本文的光伏微网系统基于三相对称,其拓扑结构如图1所示。主要组成部分有电源单元、逆变单元和LCL滤波单元。直流侧二极管D防止电流逆流,电容C防止电压突变。L1和L2为滤波电感,C1为滤波电容。
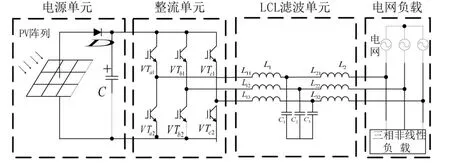
图1 三相光伏微网系统的拓扑结构图
1.2 LCL滤波器模型
在图1中选择电感L1上的电流i1,电感L2上的电流i2以及电容C1上的电压Uc为状态变量。如图2所示,在三相平衡的情况下,由KCL和KVL定理可列出状态方程,同时令直流侧电压为Uai,电网侧电压为Uao,则有
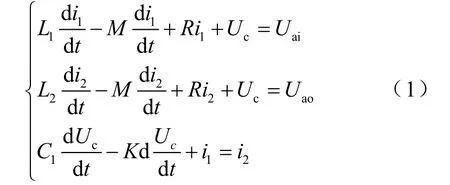
然后利用 Park公式变换,将式(1)转换到两相同步旋转d,q坐标系,则
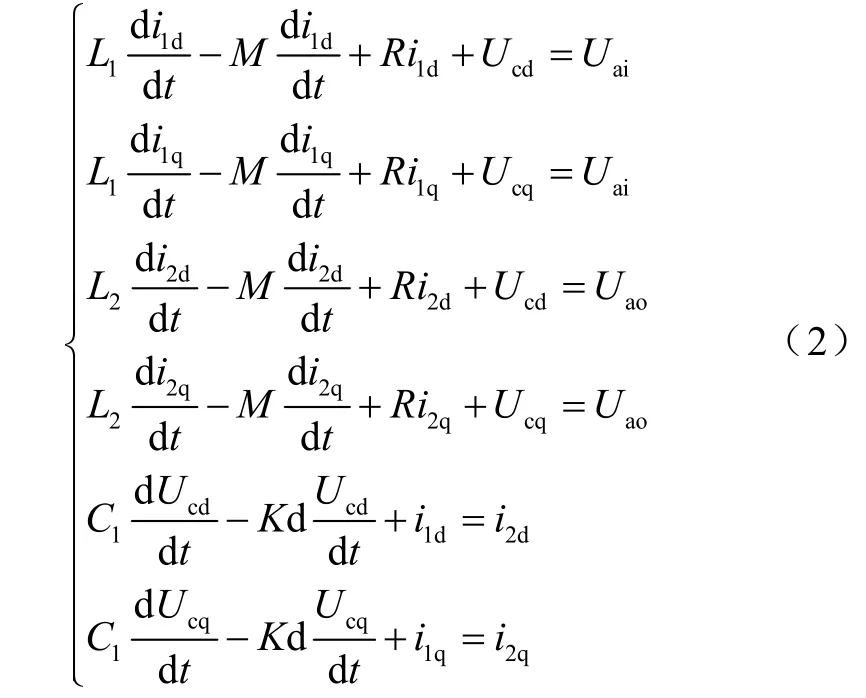
由式(2)可以得到数学模型如图2所示,即LCL滤波器在d、q坐标系下的数学模型。

图2 LCL控制器在坐标系下的数学模型
在图2中,d、q轴电流除受控制量Ud、Uq影响外,还受耦合电压和耦合电流的影响。如果引入状态反馈对这些耦合量全部进行解耦控制,不仅引入的状态量比较多,而且需进行复杂运算,这使控制相关的系统参数随之增多,使得控制性能非常依赖建模时各个参数的精确度。而此类参数对系统影响作用不大,故忽略耦合参数,将上式简化为

2 复合控制
系统输出电能的质量以及其稳定性是整个光伏微网系统重要的技术指标。由于动态响应快、收敛性良好和原理简单,近年来无差拍控制(deadbeat control)已被越来越多地应用在PWM逆变控制[11]。无差拍控制(deadbeat control)的基本思想是使系统在每一个采样点上的输出与其指令保持完全一致,不存在任何相位和幅度的偏差。无差拍控制系统中下一拍的输出量总能表示成当前周期的输入控制量和系统状态变量的线性组合。因此新装置的逆变器的状态方程和输入控制信号推算出下一个周期的输出控制量,从而理论上可以使输出电流在相位和幅值上都非常接近参考电流。从而,由负载变化或非线性负载引起的输出电流误差可在一个开关周期内得到校正。然而,单一的控制无法及时应对外界的干扰,往往不能得到高质量的电能输出。PI控制具有良好的稳定性,且原理简单,易于实现[12]。故本文提出一种电压内环无差拍控制与电流外环PI控制相结合的复合控制,具体控制如图3所示。

图3 基于LCL滤波器的复合控制框图
2.1 电压内环无差拍控制
根据无差拍控制原理,对式(2)中的d轴和q轴进行解耦,分别得到解耦后的控制单元输出指令的计算公式
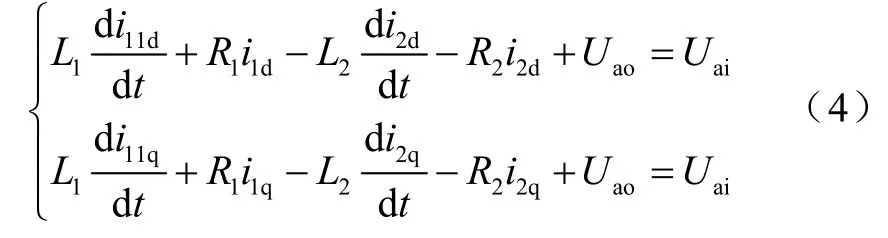
为了对指令电流进行无差拍控制,令采样周期的占空比为T,将式(4)离散化,得PWM整流器离散化后的数学模型为

将(5)式整理得


由无差拍控制可以得到PWM波形的电压指令为
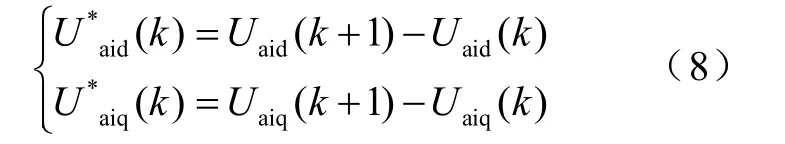
2.2 电流外环PI控制
由图1可以得到滤波单元的简化电路,如图4所示。

图4 单相光伏发电系统简化电路图
可设(L2+ R2)与C1C1并联阻抗为X,即
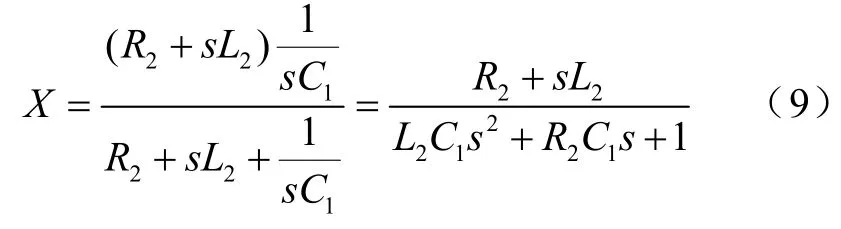
则从直流侧可以求得从整流单元的总输入阻抗为Xs,则

逆变器侧电流为i1,则

电网侧电流为i2,有

输出电压与电网侧电流之间的传递函数为

设置的主要参数有:滤波电感L1为3.05mh;滤波电感L2为9.60mh;滤波电容C1为10μF;电阻 R1为 0.81Ω;电阻 R2为 2.56Ω。由式(10)可以得到LCL滤波单元的bode图。

图5 滤波单元i2-uai传递函数bode图
由图5显而易知,在中低频段增益为一个定值,在高频段幅频增益迅速衰减;且在中低频段相位稳定在零度,具有良好的滤波效果和稳定性。
PI控制单元能对传递函数进行校正,提高滤除谐波的稳定性,则PI控制单元表示为
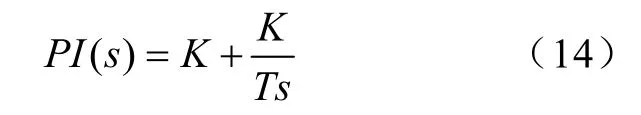
式(13)中,K为PI控制单元增益(K=0.25)。将电流环进行离散化,得到开环传递数为
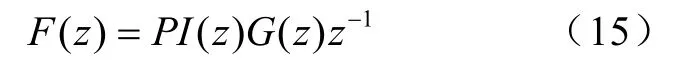
式(10)中, z-1为控制对象离散化后的传递函数,G( z)为PI控制单元离散化后的传递函数。故求得电流环的离散化闭环传函数为

其中指令电流 i*2q(k)和i*2d(k)由DSP产生,将代入无差拍控制即能实现新型复合控制。在工频电能周期内,存在各次谐波和闪变,无差拍控制能及时协调负载侧电流不稳问题,PI控制能从整体上控制光伏系统的稳定运行。故本设计控制方案能滤除各次谐波,提高了光伏微网系统的稳定性,同时大大改善了电网和负载的电能质量。
3 实验仿真
为了验证上述理论的正确性,通过新系统结构和数学模型的详细推导,可以利用Matlab/Simulink对新系统建立仿真模型。仿真结构模型令太阳发电直流侧电压为400V,负载为三相非线性负载。
图6(a)是基于传统的控制下得并网逆变器输出的电流波形图,图6(b)是基于本文的控制方案的输出电流波形图;从图 6、图 7可以看出本文控制方案能滤除各次谐波。通过仿真显而易得,传统光伏发电的A相电流总谐波失真(THD)为7.22%,而本文提出的控制方案下得电流谐波总畸变率为4.61%,如图6所示。

图6 负载输出侧电流波形

图7 直流侧电压流波形
对上图输出电流进行频谱分析,从图中显而易得,本文的控制方案更具滤除高次谐波的明显优势。
4 结论
综上所述,在配电网中,本文提出的基于无差拍控制和PI控制相结合的控制策略既克服了APF成本高和功能单一的缺点,又能更有效地滤除三相光伏发电中的各次谐波,有效地降低了并网电流的波形畸变率,提高了电网的电能质量和系统的稳定性。
[1]KADRI R, JEAN-PAUL, GAUBERT, CHAMPENOIS G,MOSTEFAI M. Design of a single-phase grid-connected photovoltaic system based on deadbeat current control with LCL filter[C].IEEE Power Electronics and Motion Control Conference, 2010(14):147-153.
[2]王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,1998.
[3]魏星,肖岚,等.三相并网逆变器的LCL滤波器设计[J].电力电子技术.
[4]李练兵,赵志国,赵昭,等.基于复合控制算法的三相光伏并网逆变系统的研究[J].电力系统保护与控制,2010(11):44-47.
[5]张亮,蔡旭,等.并联型有源电力滤波器设计及并网冲击电流的抑制.[J]电机与控制学报,2010(3):39-44.
[6]刘飞,查晓明,等.基于极点配置与重复控制相结合的三相光伏微网系统的并网策略.[J].电工技术学报,2008(12):130-136.
[7]张辑,魏盛彪,孙祖明.SVPWM 整流器的无差拍控制技术[J].制造业自动化,2010(3):236-239.
[8]夏向阳,龚芬,周峰.配电网中分布式并网发电装置的复合控制策略[J].高电压技术2011,37(8):2010-2015.
[9]夏向阳,罗安.单独注入式有源滤波器的整体优化设计[J].高电压技术,2009,35(5):1137-1143.
[10]袁性忠,王婷,朱俊星.有源电力滤波器无差拍控制策略的研究[J].电力电子技术,2010(4):38-47.
[11]刘胜荣,杨苹,肖莹,等.两级式光伏并网逆变器的无差拍控制算法研究[J].电力系统保护与控制, 2010(4):26-29.
[12]全晓明,申群太.基于 DSP无差拍控制的逆变电源研究[J].现代电子技术, 2009(9).

