基于响应面方法的转向梯形优化设计
唐应时,朱彪,朱位宇,姜友清
(1. 湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082;2. 株洲易力达机电有限公司,湖南 株洲,412002)
汽车的转向系统在车辆行驶过程中,对整车的操控性、稳定性以及轮胎的磨损都有很大的影响。同时,车辆在实际的转向过程中,也受悬架系统的结构及其与转向系统之间的相互作用有关[1]。因此,研究与分析转向和悬架之间的关系,对转向机构的设计有着非常重要的作用。当悬架跳动时,转向梯形对前轮定位参数中的前束角的变化影响最为明显[2]。因此在优化转向梯形时,必须考虑前束角的变化。文献[3]在优化断开式转向梯形时将转向系统投影在平面上,使用作图法来解决。文献[3-5]建立了断开式转向机构的平面数学模型。文献[6]建立了断开式转向机构的空间数学模型,利用 MATLAB优化工具箱单纯对转向系统进行优化。本文作者利用ADAMS/CAR建立了完整的双横臂扭杆悬架转向的虚拟样机模型,进行了对阿克曼误差和前束角的 2次仿真实验。并通过在ADAMS/Insight中进行了DOE实验分析,选用响应面方法(RSM),拟合出变量与阿克曼误差、变量与前束角之间的回归函数,进一步研究了变量与转向梯形以及前束角的关系,同时避免了复杂的公式推导与计算。最后利用 MATLAB优化工具箱,优化转向梯形,优化了阿克曼误差,并减少了前束角的变化范围,达到较好的效果。
1 转向梯形的设计要求
汽车在转向时,要保证四轮做纯滚动,各车轮必须围绕同一个瞬心转动,即必须满足阿克曼转向原理。如图1所示,阿克曼几何学原理要求将整车投影到一个平面上,当前轮在转向时,内外轮必须符合如下关角,iδ为内侧转向轮转角,L为车轮轮距;tkp为主销轴线与地面交点间的距离。
由于在实际转动过程中,车辆的转向梯形很难在整个转动范围内均满足该条件,通常只是近似地满足[7]。独立悬架车辆的转向梯形断开点位置选择不合适时,易导致转向杆系与悬架导向机构运动不协调,汽车在行驶过程中就会出现前轮摆振、跑偏等现象,破坏操纵稳定性,加剧轮胎磨损[8-9]。因此在设计转向梯形的时候,就必须使车轮在转动过程中,尽量满足阿克曼原理,从而减少轮胎的磨损,提高转向的性能。
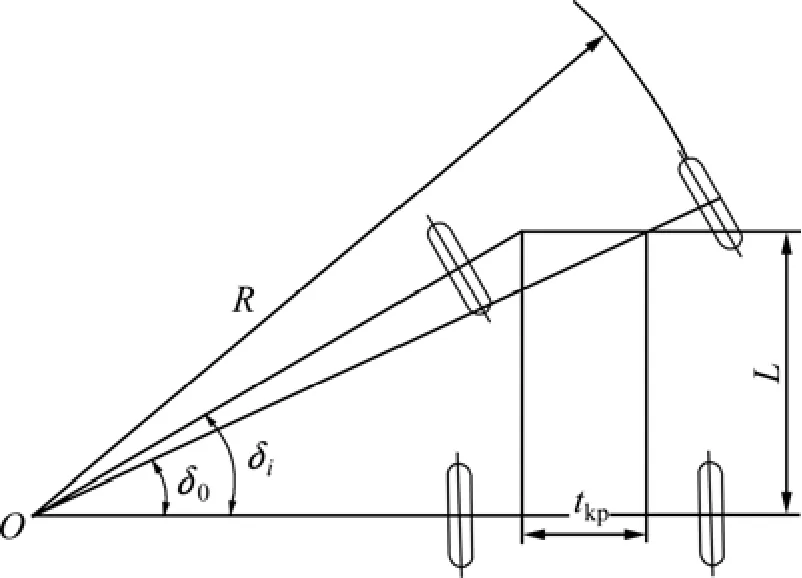
图1 理想阿克曼转向原理示意图Fig.1 Schematic diagram of ideal ackerman steering
汽车直线行驶时,若车轮跳动时,会引起前束角的变化。前束角的变化范围过大会带来滚动阻力增大,轮胎磨损增加和直线行驶能力变差等不良后果。转向梯形的内外球头的位置对前束角的变化有着较大的影响。因此在设计和优化转向的过程中,必须同时考虑前束角的变化范围[10]。
2 虚拟样机模型建立与仿真
2.1 双横臂扭杆悬架转向模型的建立
本文是以某款小型皮卡车为研究背景,该车前悬架为双横臂扭杆的独立悬架,扭杆的刚度为线性刚度,转向系统采用的是无助力的机械式齿轮齿条转向。轴荷分配为前轴50%。如表1所示,整车参数以及前轮定位参数。
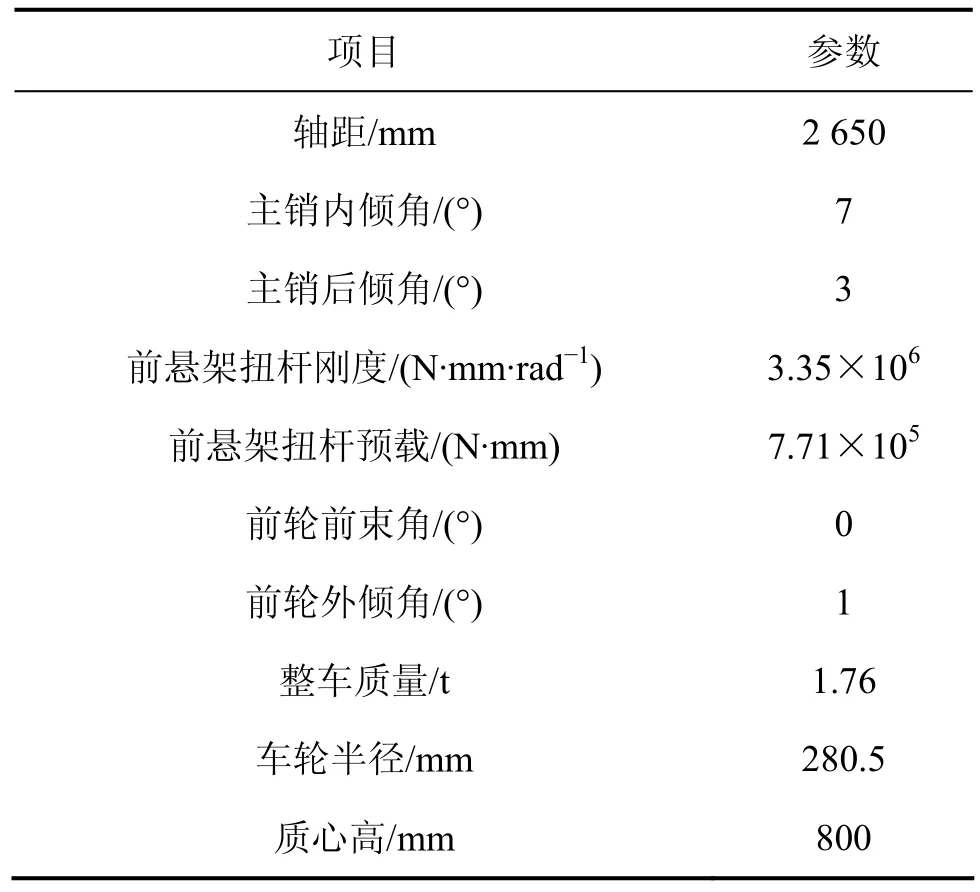
表1 整车主要参数Table 1 Main vehicle parameters
图2所示为转向和前悬架模型。在ADAMS/CAR中建立了虚拟样机模型。
2.2 虚拟样机仿真
2.2.1 车轮转向仿真分析

图2 转向和前悬架模型Fig.2 Model of steer and front suspension system
该皮卡的齿轮齿条的最长行程为68 mm,根据此参数对该模型做转向分析。可以避免由于齿轮齿条的传动比设置不准确而带来的误差。输入齿条行程,使车轮向右转动,测试在此车轮转动工况中的阿克曼误差。阿克曼误差定义为外轮的实际转角与阿克曼理想转角之差。图3所示为左轮阿克曼误差与左轮转角的关系。阿克曼误差为正时,表示外轮实际转角大于阿克曼理论值;反之,则表示小于理论值。由于汽车在正常行驶过程中,常常在0°~25°的转角范围内转向,所以保证这一范围内具有较小阿克曼误差具有更重要的实际意义[11]。

图3 左轮阿克曼误差与左轮转角的关系Fig.3 Gragh of Ackerman error vs left steer wheel angle
2.2.2 平行轮跳仿真分析
根据该车实际运行工况,选择激振台对前悬架模型进行上下轮跳动的幅度为80 mm的平行轮跳实验,用于测试在此工况下前束角的变化情况。通过ADAMS/CAR的仿真分析,如图4所示,得到左轮的前束角的变化曲线。由于曲线关于原点对称,所以在该图中只表示了车轮上跳的曲线。
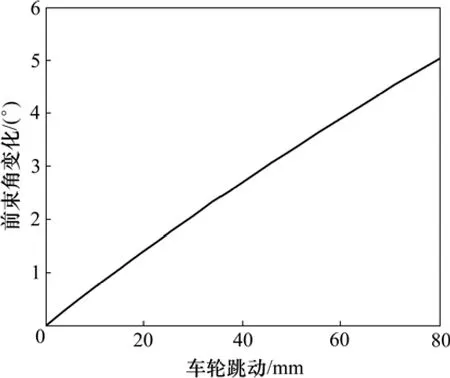
图4 前束角变化曲线Fig.4 Change of toe angle
3 DOE实验设计及设计变量的选取
DOE(Design of Experiments)实验设计方法,是一种通过实验设计和安排,利用数理统计工具来规划实验、分析模型与数据的一种方法。DOE能够以较小的实验规模,较短的实验周期和较低的实验成本,获得较为理想的实验结果,得出科学的结论[12-13]。
通过ADAMS/Insight的DOE分析,能够更好地了解转向梯形的硬点与阿克曼误差,以及与前束角之间的关系。将2次实验导入至ADAMS/Insight 软件,进行进一步的分析[14]。
3.1 转向阿克曼误差的影响因子分析
将转向仿真分析导入ADAMS/Insight,选取转向梯形的内外球头的3个方向上的硬点坐标为变量,以阿克曼误差的均方根为目标,进行 DOE实验分析。其中汽车前进的反方向为X正方向,汽车前进的右方向为Y正方向,竖直向上的方向为Z的正方向。如表2所示,得到该6个变量对阿克曼误差的相对影响因子。相对影响因子为影响值与初始目标值之比,初始目标值是在所有变量均为初值时计算得出的目标值。其中正的相对影响因子表示正相关,负的相对影响因子表示负相关,相对影响因子的绝对值越大,表示改变引起的变化范围也越大,超过 100%的相对影响因子的变量表示该变量的引起的目标值的变化范围较大,且影响值大于初始目标值。从而可以从相对影响因子看出变量的变化对目标值变化的影响度以及重要程度[15-16]。

表2 硬点坐标值对阿克曼误差的影响Table 2 Influence of points coordinates on Ackerman error
3.2 前束角变化的影响因子分析
将前束角的仿真分析导入ADAMS/Insight,选取转向梯形的内外球头的 3个方向上的硬点坐标为变量,以前束角在向上轮跳时的最大值为目标,进行DOE实验分析。表3所示为硬点坐标值对前束角变化的影响。
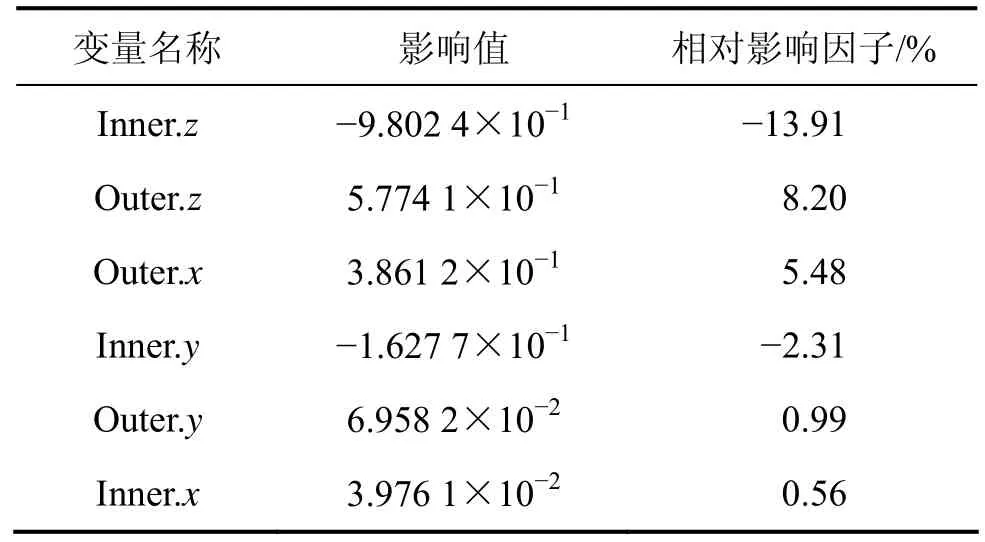
表3 硬点坐标值对前束角变化的影响Table 3 Influence of points coordinates on toe angle
3.3 设计变量的选取
从表2和3可以看出:这6个变量对转向以及前束角变化的影响。其中Inner.y对于转向的影响非常小,对前束的变化的影响也较小,考虑其受转向器零件尺寸的影响,很难随意改变,其余5个变量对于阿克曼误差以及前束的影响各有不同,故选取除此变量外的其余5个变量为设计变量,来优化转向梯形。将外球头硬点X,Y和Z方向坐标,内球头硬点X方向坐标、Z方向坐标分别设置为变量x1,x2,x3,x4和x5。
4 基于响应面方法的优化
响应面方法(RSM)是数学方法和统计方法结合的产物,通过一系列的多项式拟合来近似代表一个目标响应面。响应面法能够拟合出一个近似的包含所需变量的函数来描述响应值。由于响应面法仅输出描述关于变量和目标函数关系的函数,依靠目标函数本身的性质确定最优解,拟合出较高精度的响应关系,所以响应面法广泛地应用于设计和优化过程中。
对于具有输入和输出的线性系统,响应R和输入f1,f2,f3,…,fn之间存在着函数关系式:
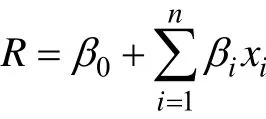
或者对于更复杂的模型,采用线性模型不能准确地描述响应曲面,可以采用二次函数来近似地描述:

响应面方法是以拟合面的方式进行的,如果拟合面跟目标函数充分近似,则拟合面的分析近似等于实际系统的分析。如果用适当试验设计来收集资料,模型参数就可有效地被估计。
4.1 转向模型拟合
本次转向模型拟合选取5个变量,目标为转向工况下阿克曼误差均方根值,采用二次函数来拟合目标函数,研究策略采用的是DOE Response Surface,DOE设计类型为全变量设计,共进行243次仿真。得到以下拟合函数:

4.2 前束角模型拟合
本次前束角模型拟合选取5个变量,目标函数为轮胎上跳工况下最大前束角,采用一次函数来拟合目标函数,研究策略采用的是DOE Response Surface,DOE设计类型为全变量设计,共进行32次仿真。得到以下拟合函数:

4.3 分析模型的拟合准确性
转向模型拟合后,经检验多重相关系数的平方R2为 0.996 481,多重样本相关修正系数164,表明该函数(1)能够很好地拟合响应曲面。
4.4 优化
根据拟合函数,以阿克曼误差均方根的最小值为目标,以前束角的最大值,和变量的边界约束条件为约束,使用 MATLAB优化工具,用阿克曼误差的均方根值作为目标函数,前束角作为约束,得到优化结果。优化前后变量如表4所示,优化结果如图5和6所示。阿克曼误差在车轮转角为0°~25°时显著减小,阿克曼误差的均方根减少了51.27%;前轮跳动时的最大前束角减小为4.5°,减少10%。

表4 优化前后变量对比Table 4 Change of factors
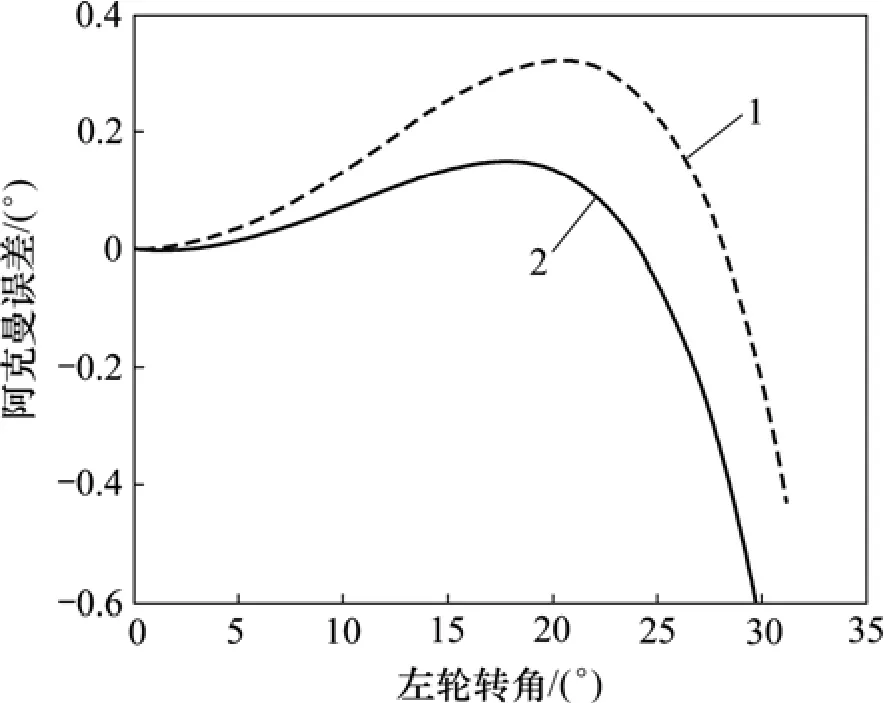
图5 阿克曼误差变化优化前后对比曲线Fig.5 Changes of Ackerman error before and after optimized

图6 前束角变化曲线Fig.6 Changes of toe angle vs wheel’s jumping before and after optimizing
5 结论
(1) 优化梯形机构的转向运动学,改善了前束角的变化特征。在前束变化范围减少10%的约束前提下,常用角度阿克曼误差减少51.27%。
(2) 此方法在考虑整车参数、悬架参数以及前轮定位参数的前提下,得到了转向梯形硬点与阿克曼误差、前束角变化的拟合函数关系,保证了准确性与实用性,并避免了繁琐的数学推导计算。
[1] 喻凡, 林逸. 汽车系统动力学[M]. 北京: 机械工业出版社,2005: 259-268.YU Fan, LIN Yi. The vehicle dynamic[M]. Beijing: China Machine Press, 2005: 259-268.
[2] 上官文斌, 王江涛. 全地形越野车前双横臂独立悬架与转向系统的设计分析[J]. 汽车工程, 2008, 30(4): 345-348.SHANGGUAN Wen-bin, WANG Jiang-tao. Design and analysis of double-wishbone suspension and steering systems of an all terrain vehicle[J]. Automotive Engineering, 2008, 30(4):345-348.
[3] 王望予. 汽车设计[M]. 北京: 机械工业出版社, 2004:249-254.WANG Wang-yu. Automotive design[M]. Beijing: China Machine Press, 2004: 249-254.
[4] 张立国, 宁国宝. 汽车断开式转向梯形机构的优化设计[J].机械设计与制造, 2007(12): 1-3.ZHANG Li-guo, NING Guo-bao. Optimal design for Ackerman steering linkage of car[J]. Mechanical Design and Manufacture,2007(12): 1-3.
[5] 姚明龙, 王福林. 车辆转向梯形优化设计及其求解方法的研究[J]. 机械设计与制造, 2007(5): 24-26.YAO Ming-long, WANG Fu-lin. The optimal design of steering trapezoidal mechanism of vehicles and the research of solution method[J]. Mechanical Design and Manufacture, 2007(5):24-26.
[6] 陈俊, 戴桂珍, 夏国林. 断开式转向梯形机构设计及优化[J].汽车科技, 2008(2): 23-26.CHEN Jun, DAI Gui-zhen, XIA Guo-lin. Optimal design for Ackerman steering linkage[J]. Automotive Science and Technology, 2008(2): 23-26.
[7] Yamakawa J, Watanabe K, Yasuda Y. Turning characteristics of articulated tracked vehicles. Vehicle characteristics and steering performance[J]. Transactions of the Japan Society of Mechanical Engineers C, 2001, 67(657): 1544-1551.
[8] Reimpell J. 汽车底盘基础[M]. 张洪欣, 余卓平, 译. 北京:科学普及出版社, 1992: 154-158.Reimpell J. Automotive chassis elements[M]. ZHANG Hong-xin,YU Zhuo-ping, transl. Beijing: Popular Science Press, 1992:154-158.
[9] Reimpell J. 汽车行驶性能[M]. 黄锡朋, 谢春阳, 译. 北京:科学普及出版社, 1992: 89-92.Reimpell J. Automotive driving ability[M]. HUANG Xi-ping,XIE Chun-yang, transl. Beijing: Popular Science Press, 1992:89-92.
[10] Cherian W, Jalili N, Haque M. Development of a non-linear model of a double wishbone suspension for the characterization of force transmission to the steering column and chassis[C]//Proceeding of ASME(2004). International Mechanical Engineering Congress and Exposition. California, 2004:775-780.
[11] 刘惟信. 汽车设计[M]. 北京: 清华大学出版社, 2004:503-504.LIU Wei-xin. Automotive design[M]. Beijing: Tsinghua University Press, 2004: 503-504.
[12] Grove D M, Davis T P. Engineering, quality and experimental design[M]. England: Longman Pub Group, 1992: 28-48.
[13] Schneider T, Fielke J M. Simulating the cornering behaviour of multiple trailed implements[J]. Biosystems Engineering, 2008,100(3): 355-361.
[14] 唐应时, 占良胜, 严仁君. 重型汽车双前桥转向系统的运动学和动力学的建模与仿真分析[J]. 湖南大学学报, 2003, 30(3):59-61.TANG Ying-shi, ZHAN Liang-sheng, YAN Ren-jun. Kinematics and dynamic simulation of double front axle steering of heavy vehicle[J]. Journal of Hunan University, 2003, 30(3): 59-61.
[15] 蒋国平, 王国林, 周孔亢. 独立悬架转向梯形断开点位置的优化设计[J]. 农业机械学报, 2007, 38(2): 30-34.JIANG Guo-ping, WANG Guo-ling, ZHOU Kong-kang.Optimization design of splitting point of Ackerman steering linkage of independent based on Adams[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(2): 30-34.
[16] 周兵, 杨凡, 徐琪. 基于 ADAMS的转向机构的优化设计[J].湖南大学学报, 2008, 35(12): 23-26.ZHOU Bing, YANG Fan, XU Qi. Optimal design for steering linkage base on ADAMS[J]. Journal of Hunan University, 2008,35(12): 59-61.

