基于Poisson圆盘分布的河流仿真技术

冉 剑 丁 莹

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

在虚拟现实领域中，基于物理规律的河流实时仿真是对自然景物仿真的一个难点.河流仿真既不同于对大面积水域的仿真那样体现全局观察的效果，比如海面、湖泊等;也不同于局部的流体运动仿真分析那么细致，比如水滴落入水面、水中气泡细微的现象等.河流仿真的关键之处是体现河流的流动性和河面的纹理描述及纹理重构.

现存的一些研究有的比较注重仿真效率，会采取某种三维技术达到以假乱真，但是缺少流体运动规律的支持，难以满足高真实感的图像效果;有的通过求解流体力学N-S(Navier-Stokes)方程实现，但是求解过程复杂，难以达到对实时性的要求.近年来，文献［1］采用流体求解器，获取并解算流体与地形的交互信息，并使用运动的过程化纹理来表现河流的流动，在仿真大规模河流视景中有一定代表性;文献［2］通过边界四边形的方法划分河流区域，并绘制Bézier曲线来描述河流的走向，把河流区域的像素投射在曲线上执行渲染.该方法摒弃粒子系统，较好地控制了计算复杂度.

本文提出的方法既要考虑满足河流运动的物理规律，得到更加逼真的河流视景，又要考虑到仿真的实时性要求，即通过求解得到在有边界条件的约束下的二维平面流的速度场，并采用Poisson圆盘分布技术，高效的纹理精灵渲染技术，对河流运动的过程进行实时的三维渲染.

1 Poisson圆盘分布

Poisson圆盘采样是一种由最小距离准则限制的一致性采样过程，在一定的空间随机分布的采样点，点与点之间的距离大于某个阈值，同时也不能再加入一个点，否则该点必然与某个现存其他点的距离小于阈值，导致违背最小距离准则.

以往的Poisson圆盘分布算法的效率主要受限于点的数目的增加，当采样点的数量比较大的时候，低下的计算效率难以满足计算机仿真对实时性的需求.如经典采样方法Dart-Throwing算法［3］有它的弊端，因为每次采样产生的点都是在［0，1］n(n=2，3)区域中的随机位置，这样随着采样点数的增多，产生无效点的几率就会随之增加，从而大大增加了算法复杂度.

文献［4］提出的算法的复杂度和采样点的数量能够达到线性的时间关系.根据文献［4］的思想，本文提出一种相对简练的算法实现.基本的思路是:在已经存在的点集的基础上不断产生新的采样点，新的点只能出现在现存点集的邻域中，同时满足Poisson圆盘分布的最小距离准则.这里要使用一个平面网格辅助采样点的产生，同时需要生成两张表，一张表用来跟踪所要产生的点，一张表用来跟踪需要处理的点.算法的细节描述如下:

1)创建一个网格(grid)使得每一个单元格(cell)最多只能容纳一个采样点，如果指定的点与点之间的距离必须大于等于r，那么令单元格的大小为r/2.

2)第1个点随机产生，然后把它置于输出列表、待处理列表和栅格中.

3)执行下面操作，直到待处理列表为空:

①从待处理列表任意选取一个点;

②对于这个选取的点，在它周围的环面，随机地选取30个点，之所以选择30是因为能得到较好的分布效果;

若点的数量较大，则使得点聚集比较紧密，但同时会影响到计算效率.在这些点集中，对于每一个产生的点:使用栅格检查是否距离参考点比较近;如果没有这样的点，把这个点添加到输出列表、待处理列表和栅格中;

③把这个点从待处理列表中移除.

4)把返回输出列表中的点集作为得到的采样点.

图1展示了如何在一个现存点的周围产生一个随机点，已经存在的点用圆点表示，新产生的点用三角形表示.新产生的点的位置用两个参数来描述:角度 α(随机地选择从0°～360°)，距离 R，r(和参考点的距离从Poisson圆盘分布的最小距离到两倍的该距离的范围随机变动).

图1 产生新的采样点

当一个新产生的点被容许作为采样点之前，必须确保之前产生的点(圆点)不会离它太近.图2显示了网格的一部分，其中三角形是有可能成为新的采样点的“潜力点”，为了达到上面的要求，必须针对现存点检查被圆形区域(即那些位于新产生的点的周围的4个角落处)覆盖的这样一块区域.其中正方形区域为部分或者全部被圆圈所覆盖的单元格，只需要检查这些单元格即可.

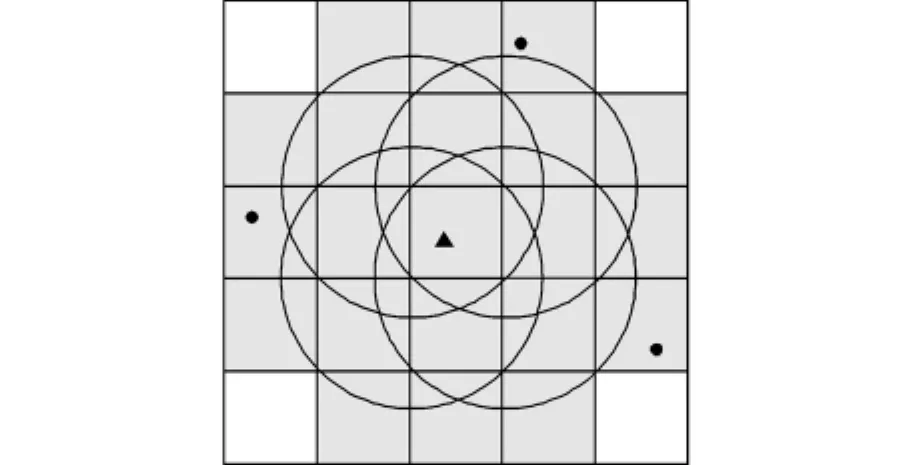
图2 检查潜在采样点的邻域

2 纹理精灵

在场景的渲染实现中，纹理的使用是十分重要的，能够增加表面的细节而避免增加场景几何的复杂性.一些研究人员通过图像采样去合成大块的纹理，许多表面有各向同性的外观，所以能够通过小范围的采样很好地捕捉.然而基于小块纹理混合的方法缺少有效的表述，它们经常在大的图像中存储结果纹理，这样很浪费内存.本文采用一种纹理精灵［5］的表达方法.使用这个表达能以很高的性能给几何体添加纹理，它使用很低的内存损耗，也没有必要考虑全局纹理的参数化.使用许多小的纹理精灵去混合构成一个全局的复杂的纹理，并且这些小的纹理元素都有自己的属性，比如位置、大小、材质属性、ID值等，而且这些属性可以动态的更新，因而它们能提供一个很方便的框架来做交互的编辑和运动纹理.

在实时渲染中，通过片段着色器程序(fragment program)去计算某一时刻每一个像素上是由哪些纹理精灵覆盖，从而计算出全局的外观纹理效果.具体实现时，首先生成物体表面的参考纹理，然后按照指定的采样函数采样参考纹理，这样就得到了每一个纹理精灵元素，再结合纹理混合技术有效地混合和渲染这些精灵元素.

在渲染的时候，可以用两张表来存储纹理元素:第1张表对应的是在屏幕空间的间接的网格，每个网格里存储覆盖它的纹理精灵元素的索引，或者不存储元素则为空;而纹理元素的参数则存在另一个表中，称之为精灵参数表.这些纹理参数包括纹理元素在世界空间的位置，纹理元素的纹理坐标，混合权重因子等等.这两张表都可以编码到纹理中，以便于GPU(Graphic Processing Unit)做并行计算.最后就可以把元素的集合当成一个普通的纹理来处理，应用在实体对象上.表面混合重构的算法描述如下:

3 河流仿真过程

计算河流流动的表面的速度场，计算速度场的边界条件来自河道两边真实的河岸.这里考虑到求解N-S方程的复杂性，本文引入二维流体的势流理论中的流函数［6］φ的概念.流函数的定义是:二维平面流中流过任意两点间的单位体积流量等于这两点的流函数值的差值.流函数的偏导数即速度矢量分量，这样在二维平面流的计算中，求解任意一点流函数的偏导数就可以得到速度:

河流中的任意一点流函数求取:根据流函数的定义可知，由于河流不会在河岸边界上有法向的速度值，所以流函数在边界上为常值.指定左、右边界的流函数值φl和φr，因为在离边界近的地方河流的流动受边界的影响大，在离各个边界远的地方河流的流动受其影响小.所以本文提出的插值方法为反比权重插值，公式如下:

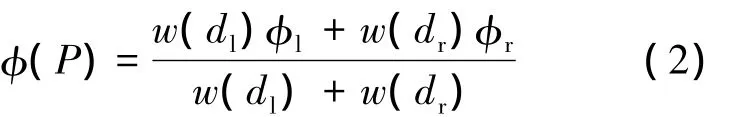
式中，P为河流中任意一点的坐标;dl和dr为P点到左、右边界的距离;w为边界对点P的反比影响因子.

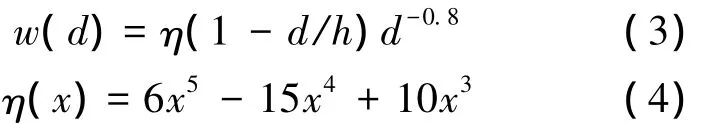
式中，h为河流的最大宽度;η为多项式，保证P点在边界处流函数值是连续的.

根据以上思路结合公式，由某一点到边界的距离求得边界影响因子;按照插值公式可计算出该点的流函数值;通过差分算法可以得到该点的速度矢量，从而得到河流表面的速度场.

有了河流的速度场以后，在屏幕空间做Poisson圆盘分布的采样，将得到一系列采样点，如图3所示.从摄像机镜头出发以这些点为起点做射线查询，射线与河流表面交叉会得到两种点:①投射到河流内部的采样点;②陆地上的采样点.通过计算得到的河流的速度值来运动内部的点，就得到了河流运动的显式表述.最后进行河流的渲染，采用上述的纹理精灵的技术，在每一个采样点上附着对应位置上查询的水波纹理，当这些水波纹理元素运动的时候，在每一帧通过Poisson圆盘重采样，并采用纹理重构的技术来合成渲染在河流表面的全局水面纹理.仿真过程实现如下:

1)在每一帧，当Poisson采样点按照河流的速度场平流后，投射在河流内部的采样点和在陆地上的采样点之间就不再满足Poisson圆盘分布准则，这时候就需要对这一帧的粒子进行处理，以满足在下一帧开始之前所有屏幕上的采样点仍然满足Poisson圆盘分布的样式.所以，在上一帧结束时，需要对现存的点进行重采样:删除某些不满足Poisson圆盘分布的点，即离其它点太近的点;同时河流沿着河道流动，必然有一部分代表流体的点平流到视锥外，另一部分平流进入视锥，产生新的点，自始至终，在屏幕空间通过这些点的运动构成来描述河流整体的运动.算法描述如下:

图3 屏幕空间Poisson采样点的产生

2)水波纹理精灵取自河面的真实纹理，同时加入噪声扰动，河流表面首先渲染到一段帧缓存中，然后采用适当的连续的纹理函数去采样该纹理，就得到具体某一时刻、世界空间中某一位置的大小为圆盘半径R的圆形纹理(正视图)，或者椭圆形纹理(透视图)，这些椭圆形纹理的中点在屏幕空间仍须满足Poisson圆盘分布形式，即是圆形的纹理投影.某一点P的纹理采样函数为

式中，ui为水波精灵元素的纹理坐标;pi为P点在世界空间的位置;x为纹理采样的位置自变量.

在这一步中需要使用上一步所计算得到的粒子的世界空间的坐标来接口被采样的参考纹理.

3)每一帧中都需要这些纹理精灵整体构成一个全局的水面运动的纹理，所以要保证全局纹理的频谱一致性，既不能出现有河流没有被纹理元素覆盖的部分，同时又不能在某些像素上纹理元素的覆盖太多;本文很好地利用了Poisson圆盘分布的优点.本文采用片段着色器逐像素计算所覆盖的纹理元素的累加，就得到河流在屏幕上像素的颜色值.河流表面的三维描述可以表示成连续的纹理函数:

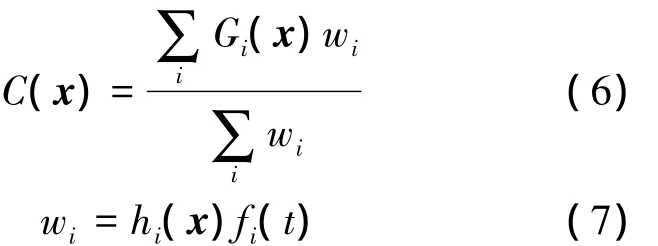
式中，wi为自定义的权重因子，wi的定义要保证在任何一个河面点对应屏幕空间的像素都至少包含一个纹理元素;i为覆盖在某一像素上的纹理精灵元素的个数;hi为光滑核函数用来确保纹理的连续性控制;fi为时间函数，控制插入和删除粒子的生命周期.

为了表现河流水面的波纹大小等效果，本文考虑通过改变参考纹理的种类来实现.采样不同的振幅或者频率的水波纹理来产生不同的河面渲染效果.最后加上其他着色效果，比如折射反射等，这些技术主要用于表现河流的光影效果.

图4为最终的渲染结果，在Release模式下的帧率可以达到90帧/s.

图4 河流最终渲染结果

4 结论

本文提出了一种Poisson圆盘分布的算法，实现屏幕空间的优秀的粒子分布样式，通过粒子的运动显式地描述河流表面的速度场;结合采用纹理精灵采样技术，采用两张表接口纹理数据，通过纹理的动态查询和纹理精灵的混合，有效地实现对河流表面的渲染.实验证明该算法很好地提高计算效率，减少了纹理存储负担，在满足高真实感图形渲染效果的同时保证了足够的仿真实时性.

References)

［1］Burrell T，Brooks S，Arnold D.Advected river textures［J］.Computer Animation and Virtual Worlds，2009，20(2/3):163－173

［2］Hendrickx Q，Smelik R，Bidarra R.Real-time rendering of river networks［C］//Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games.New York:ACM，2010:No.22

［3］McCool M，Fiume E.Hierarchical Poisson disk sampling distributions［C］//Brooth S K，FournierA.Proceedingsofthe Conference on Graphics Interface'92.San Francisco:Morgan Kaufmann Publishers Inc，1992:94－105

［4］Dunbar D，Humphreys G.A spatial data structure for fast Poisson-disk sample generation［J］.ACM Transactions on Graphics，2006，25(3):503－508

［5］罗林.2D游戏中的精灵管理［J］.科技创新导报，2009(23):176 Luo Lin.Sprites managering in 2D games［J］.Science and Technology Innovation Herald，2009(23):176(in Chinese)

［6］White M F.Fluid mechanics［M］.Columbus:McGraw-Hill，2001:238－245