牛顿与莱布尼兹和他们的微积分评述*

□赵坚

(大同煤炭职业技术学院，山西 大同 037003)

数学研究的许多新的、广泛的领域是在17世纪开辟的，使得这个时期成为数学发展中最富有成果的时期。无疑，其中最值得注意的成就就是接近该世纪末牛顿和莱布尼兹作出的微积分的发明。有了这个发明，创造性的数学相当普遍地发展到一个高级的水平，使初等数学的历史基本结束。几乎可以这样说，今天如果一个人没有这方面的知识，就不能说他很好地受过教育。

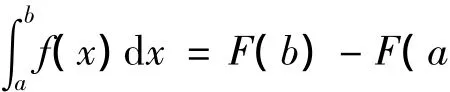
一 牛顿和他的流数法

伊沙尔·牛顿于1642年(旧历)出生于沃尔斯索普村。他的父亲是个农民，在牛顿出生前就死了，他计划让牛顿也务农。而幼年的牛顿在设计灵巧的机械模型和做实验上，就显示出才能和爱好。18岁时被允许进入剑桥大学三一学院。

由于牛顿在斯托桥的集市上偶然碰到一本占星学的书，引起了他对数学的兴趣，他先读欧几里德《原本》，然后看笛卡尔的《几何》，这有些困难。他还读奥特雷德的《入门》、刻卜勒和韦达的著作，以及沃利斯的《无穷的算术》。他从读数学到研究数学，开始发现推广的二项式定理，并且创造其流数法(微积分的另一种表述)。

从1665年夏末到1667年夏末，由于鼠疫流行，剑桥大学停了课。牛顿住在伍尔斯托普的家中，研究其数学(过曲线上任意点作其切线，和计算其曲率半径)，并有兴趣于各种物理问题，作他的第一个光学实验，并将其万有引力理论的基本原理系统化。但也有研究表明，这种说法是虚构的，但牛顿本人为了保证其在微积分发现中的首要地位，也散布这种说法，即在1666年剑桥大学短期复课之前，他已做出了这些发现。

当牛顿开始他18年的大学教授生活后，他的第一个研究是关于光色的，后来以一篇论文的形式由皇家学会发表。但引起一些科学家的猛烈攻击，牛顿感到很无聊，发誓再也不发表任何关于科学的东西了。这对数学史产生了重大影响，几乎所有他的发现都在许多年后才发表。也就引出了后来他与莱布尼兹在微积分发现的优先权上的争论。

他的《流数法》写于1671年，直到1676年才发表。在这部著作中，牛顿把一条曲线看作是由一个点的连续运动生成的。按照这个概念，生成点的横坐标和纵坐标，一般是变动的量。生成的量被称作流，流的变化度称为它的流数。如果一个流(比如生成一条曲线的点的纵坐标)用y表示，则这个流的流数用表示。我们知道:用现代的符号，这等价于dy/dt，在这里，t表示时间。尽管在几何中引进了时间，但我们还是可以凭借假定某量(比如，动点的横坐标)依固定比率增加，把时间的概念躲过。某流增加的固定比率称为主流数，可以将任何其它流的流数与主流数比较。的流数被记作;对于高次流数，如此类推。另一方面，流量y通过在符号y周围画一小正方形表示，或者有时也用表示。牛顿还引进另一个概念，他称之为流的矩，它指的是流(例如x)在无穷小的时间间隔o中增加的无穷小量。于是，流x的矩由乘积给出。牛顿指出:在任何问题中，可以略去所有包含o的二次或二次以上幂的项;这样，我们得到曲线生成的坐标x和y与它们的流数和关系的方程。

牛顿考虑两种类型问题，在第一类型的问题中，给出联系一些流的关系式，要我们找出这些流和它们的流数的关系式。这就是我们上面讲的，这自然等价于微分。在第二种类型的问题中，给出联系的一些流和它们的流数的关系式，要我们找出仅仅联系流的关系式。这是逆问题，等价于解微分方程。后来牛顿用他的初步极限概念作出根据，证明略去包含o的二次或二次以上的项是正确的。他定义极大值和极小值，曲线的切线，曲线的曲率，拐点，曲线的凹凸性，并且他把他的理论应用于许多求积问题和曲线的求长。在一些微分方程的积分中，他显示了超人的能力，在这部著作中有对代数方程和超越方程都适用的实根近似值求法(牛顿法)。

牛顿的贡献如此伟大，涉猎广泛，除了数学、物理，还包括化学、炼丹、神学的研究。所以，连莱布尼兹也说:“在从世界开始到牛顿生活的年代的全部数学中，牛顿的工作超过一半。”拉格朗日也说他是历史上最有才能的人，也是最幸运的人——因为宇宙体系只能被发现一次。他的成就被英国诗人波普用诗表达:自然和自然的规律沉浸在一片黑暗之中，上帝说:生出牛顿，一切都变得明朗。

二 莱布尼兹的微积分

莱布尼兹，是17世纪伟大的全才，在微积分的发明上，是牛顿的竞争者，于1646年出生于莱比锡城。当还是儿童的时候，就自学拉丁文和希腊文，不到20岁，就熟练地掌握了一般课本上的数学、哲学、神学和法学知识。青年时代，他开始发展他的《万能算法》;后来，发展出布尔的符号逻辑;再靠后些，1910年，发展出怀特黑德和罗素的伟大的《数学原理》。当莱比锡大学以他年轻为藉口，拒绝授予他法学博士学位时，他迁到纽伦堡。在那里，他写了一篇关于用历史的方法教授法学的杰出论文，并且把它献给美因茨的帝选侯。这导致帝选侯任命他重修一些法典。从这时起，他把大部分时间用于外事活动。

1672年，莱布尼兹在巴黎做外事工作，在此期间，他已经发现微积分的基本原理，给出此学科中的大部分符号，并且做出一些微积分的基本公式。而在汉诺威工作时，他有时间探讨他喜爱的研究，结果他写下的各种课题的论文堆成了山。只可惜他生命的最后7年，是在别人带给他和牛顿的关于他是否独立于牛顿发明了微积分的争论中难受地度过的。

莱布尼兹对其《万能算法》的研究，导出数理逻辑的理论和具有形式规则的符号法，用以避免思考的必要性。这个设想，到了近现代，才达到了令人注目的实现阶段。但是他已经用通行的术语陈述了逻辑的加法、乘法和否定的主要性质，已经考虑到空集和集的包含关系，并且指出在集的包含关系和命题的蕴含关系之间的类似性。

莱布尼兹是在1673年到1676年之间某时发明他的微积分的。1675年10月29日，他第一次用长写字母S，这个现代的积分符号表示卡瓦列利的“不可分元”之和，几周之后，他像我们今天这样写微分和微商，并有了像∫ydx和∫ydy这样的积分。直到1684年，才发表了他的关于微积分的第一篇论文。在这篇论文中，他引进dx作为任意有限区间，并且用比例dy∶dx=y∶次切距定义dy。

在我们的初等微积分课中的微分的许多基本原则，是莱布尼兹推出的。求两个函数乘积的n阶倒数的法则，现在还被称作莱布尼兹法则。他对数学形式有超人的直觉，并且对于很好地设计符号的潜在可能性很敏感。他的微积分符号已被证明是很好的，并且无疑，比牛顿的流数记号方便、灵活。而直到19世纪，在剑桥成立分析学会时，才提出来用“d”来代替“·”。

最后要说，我们不准备在这里讨论牛顿和莱布尼兹之间不幸的争论。今天普遍的意见是:他们彼此独立地发现了微积分。牛顿发现在先，而莱布尼兹发表得早。如果说莱布尼兹没有像牛顿那样对数学研究得深，但他的知识面则较广，并且，作为一个分析学家和数学物理学家他都次于他的英国对手，但他对数学形式有比较敏锐的想像力和卓越的本能。在牛顿和莱布尼兹之后的若干时间，积分的基础还是不清楚的并且很少被人注意，因为早期研究者被此学科的显著的可用性所吸引。第一本微积分课本出版于1696年，是洛比达写的。还发表了他老师约翰·伯努利的讲义，在这本书中有求分子、分母趋于零的分式的极限值的所谓洛比达法则。

［1］H·依夫斯(美)．数学史概论(欧阳绛译)［M］．大同:山西经济出版社，1986．

［2］赵文茹．高等数学［M］．北京:北京交通大学出版社，2011．