编组站堵塞情况下网络车流调整疏解方案分析

李 响 上海铁路局上海铁路股份有限公司筹备组

曲思源 上海铁路局调度所

郭 平 上海铁路局办公室

车流调整是铁路调度工作的一项重要内容。车流结构及车辆分布偏离标准是日常调整的主要原因。车流结构发生较大变化时，将造成有些线路或车站的能力紧张甚至形成堵塞。而堵塞流理论，是网络流规划理论中的非确定性、多值性研究的一个新分支，主要研究对象是网络的最大流和最小流，该理论成为研究如何防止交通网络堵塞的发生和在堵塞发生时如何疏散交通流的理论。本文应用堵塞流理论研究铁路编组站堵塞情况下的网络车流的调整问题，通过防堵塞和改善堵塞控制，为铁路网络车流调整问题提供新的思路、方法，实现车流调整的精细、动态、集约化。

1 编组站堵塞及现有网络车流调整分析

为确保网络车流流动的有序性，在货物列车编组计划中，铁路部门对各种车流规定了正常的运行径路，包括最短和特定径路。为缓解编组站堵塞状况，车流调整的一项重要措施就是改变车流运行径路。在日常调度指挥过程中，正常径路因提高通过能力技术改造施工，或因灾害和重大事故中断行车，或因车流增加以致通过能力不能负担时，须经过铁道部批准后，方可变更车流运行径路。所谓车流迂回径路就是指在日常运输工作中，进行车流调整时临时指定的经由线路，属于非正常径路。要根据迂回径路区段通过能力和机车供应情况，在能力可以负担的情况下，方可实施，尽量减少对运输秩序的干扰。目前，针对网络车流经常、实时且不可预见的变化，遇有编组站阶段性堵塞时，调度往往凭经验处置，车流调整的措施仍处于粗放和定性管理阶段，缺乏对车流调整的定量研究和精细、集约管理。特别是在迂回货列数量较多时，决策不够科学合理，运输效率反而下降，浪费迂回径路的通过能力。

2 堵塞流理论和最小车流控制的思路和方法

2.1 堵塞流理论

定义1 流出网络始点的弧 (简称入流)的容量之和称为网络的入流，即

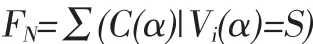
其中，FN为网络的入流；C(α)为弧α的容量；Vi(α)为弧α的始点。

定义2 当网络中不存在对于可行流ζ的正向增广路时，则称可行流ζ为饱和流：如果该饱和流的流量小于网络的入口流量，则称该网络中的饱和流ζ为堵塞流。

定义3 流量值最大的堵塞流称为最大堵塞流，流量值最小的堵塞流称为最小堵塞流。

定义4 所谓顶点A的容差φA是指所有以A为始点的有向弧的容量总和与所有以A为终点的有向弧的容量总和之差，即

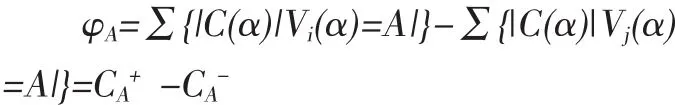
式中，Vj(α)为弧α的终点。

定义5 网络中除始点和终点外，各顶点的每个弧的容量小于或等于进入该顶点的各弧容量之和时，该网络称为规范化网络。网络规范化的方法是：当在某顶点存在流出弧的容量大于流入该顶点各弧的容量总和时，则将该流出弧的容量改为等于流入该点各弧的容量总和。

定义6 具有最小流量的饱和流称为网络最小流。

定理1从研究网络中的堵塞现象来说，在规范化网络中的流动情况与原网络中的流动情况是一样的。

定理2网络中出现堵塞的必要条件是规范化网络中存在负容差的顶点，并将其称为结构性堵塞点。

2.2 网络车流最小控制思路和方法

网络中的编组站堵塞实际上是有结构和流动的随机性和动态性造成的。编组站堵塞分为两种情况：局部堵塞和全局堵塞。局部堵塞是指网络顶点处的堵塞现象。当这种堵塞发生时，在这些堵塞点及相应的弧内聚集过多的流量，使局部成为不可行流，这时网络的总流量变小。将网络的饱和流定义为堵塞流，具有最大流值的堵塞流即是网络的最大流，它和经典网络流理论中的最大流是完全相同的一个概念；而具有最小流值的堵塞流（即最严重堵塞情况下的极值流）则定义为网络的最小流。通过改变网络的结构（关闭某些弧段）防止或者减少堵塞的发生，使得网络车流最小流尽可能提高。将最小流控制分为两种，第一种最小流控制是在改变网络结构后，最终得到的新网络的最大流和最小流相等，称其为防堵塞控制，最大流可能小于结构改变前的最大流；第二种最小流控制是在改变网络结构时，不使新网络的最大流减少而尽可能提高网络的最小流，称之为改善堵塞控制。关于网络的最大流和最小流的确定，主要有用标号法计算网络最大流，分支定界法、双向增流法和图单纯形法求解网络的最小流。

3 实例分析

现模拟上海局阜阳北和符离集站接入到乔司站及其以远重车流的调整实例并加以分析，简化的规范化网络图由两个始点和一个终点组成，如图1所示。s，v1，v2，v3，v4，v5，v6，t分别代表虚拟源点、阜阳北、符离集、合肥东、蚌埠东、芜湖东、南京东、乔司站。其中，除符离集站为区段站外，其余均为编组站；s-v2-v4-v6-s通常称为一通道，s-v1-v3-v5-s为二通道，车流调整需要一、二通道的配合才能完成；v1v2、v3v4、v5v6 为两个通道的联络线，三条联络线均为单线，通过能力紧张，需要妥善安排车流迂回径路和列车数量，车流调整的方向图1中已标出；弧上的数字表示(fü，cü)，其中 fü表示由节点i到j的流量（单位为：货物列车列数目），cü表示由节点i到j的容量。目前，因一通道是客运通道，主要运行旅客列车，需要将部分货流调整到二通道；二通道从阜阳北到乔司站全长660 km，是该重车流调整的主要通道。二通道在路局运输结构中占据十分重要的地位，沿途五个编组站均不同程度的存在等开情况较多，日常运输组织中不仅要保持二通道的畅通，还要对存在的问题需要进一步调整和优化，降低运输成本，提高运输效率。

问题是如何妥善安排一、二通道车流，合理安排好联络线的使用，达到车流精细调整的目的，确保编组站堵塞情况下网络车流的通过能力最大。

图1 网络车流简化示意图

用最大流问题的标号算法求得最大流Fmax=16（见图2），用最小流问题的分枝定界法求得最小流Fmin=13（见图3）。其中，各节点旁（）内数字表示该节点的容差，下同。

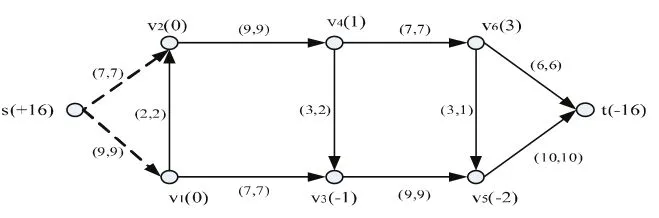
图2 网络最大流

图3 网络最小流

4.1 防堵塞控制

防堵塞控制只要存在最大堵塞截面，找到堵塞截面上的反向弧就关闭，停止条件是网络最大流与最小流相等。

图3中堵塞的路段为 v2v4，v3v4，v5v6，v5t，其中 v3v4 和 v5v6 为反向弧。因此，首先考虑关闭v3v4，其最大流F1max=13，用最小流的分支定界法求得扩容后的最小流F1min=13（见图4）；在考虑关闭v5v6，其F2max=15，可求得最小流F2min=15（见图5）；同时关闭v3v4和v5v6，可求得最小流F3max=F3min=13（见图 6）。

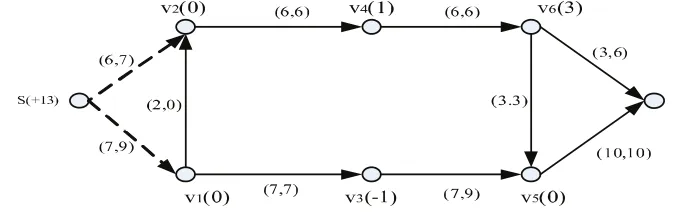
图4 关闭 后的网络最小流

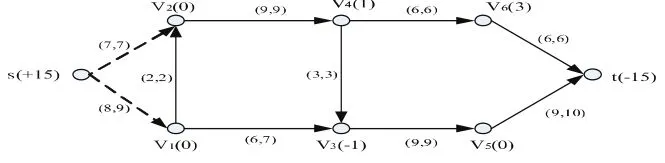
图5 关闭 后的网络最小流

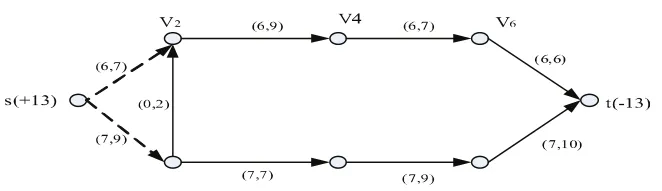
图6 关闭 、后的网络最大流及最小流

可见，关闭v5v6后的最小流值最大。图6中所示的网络中，只要从源点s流出的流量不大于13，因为网络中最大流与最小流相等，所以网络尽管存在堵塞截面，但网络不可能再发生因随机流动造成的堵塞，这是车流网络也可以称为"动态均衡"网络，可将13作为网络车流调整的阈值。当从源点s流出的流量正好为13时，尽量不采取改变车流径路的措施（图4）。存在迂回径路，主要是因为节点容差存在0的情况，最小完全截集有多解。当从源点s流出的流量大于13时，网络车流就会不同程度的发生堵塞现象，就要根据源点流入车流量的情况，相应采取改变车流径路的措施调整好相关车流，确保网络通过能力最大。

4.2 改善堵塞控制

改善堵塞控制要求反向弧关闭必须满足，该反向弧关闭后的网络最大流等于该反向弧关闭前的网络最大流。停止条件是：当存在堵塞截面，却找不到这样的反向弧，该弧的关闭不影响网络的最大流。

若采取改善堵塞控制措施，不能同时关闭v3v4和v5v6，因为关闭后的最小流值及关闭v3v4后的最小流值均比单独关闭v5v6后最小流值小，所以应当关闭v5v6，在尽量确保原网络最大流的基础上得到网络改善堵塞控制措施。

5 结束语

本文借鉴堵塞流理论，根据网络车流需求提供结构上的冗余，对编组堵塞情况的车流调整迂回径路问题做了较为深入的研究，克服经验决策，为车流调整问题提供的理论依据，确保编组站堵塞情况下车流组织的动态、集约和精细化，提高运输组织效率。同时，也是将复杂问题进行简单化处理的一种尝试。但鉴于网络随时间变化的时变性，车流调整问题变得的更为复杂，时变网络的车流调整问题有待深入研究。