Cesaro序列空间的装球常数

麻振华 张洪亮 闫常丽

（河北建筑工程学院数理系，张家口075000）

1 介 绍

2001年，崔云安和Hudzik H等人在文献［3］中给出了Cesaro序列空间的装球常数为但是证明过程比较麻烦，本文用另外一种较为简单的方法同样证明了此结果.

一般来说，我们用X表示Banach空间，B（X）和S（X）分别表示X的单位球和单位球面.定义1［4］Banach空间X中的装球常数P（X）定义为：

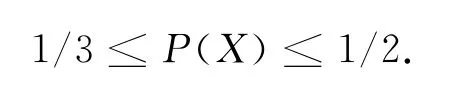
定义2［1，2，3］我们称序列为Cesaro序列空间cesp.其范数定义为

引理1［3］对任何具有Fatou性质且序连续的Kothe序列空间X，有下式成立：

2 结 果

其中

证明 由于任何Cesaro序列空间都是具有Fatou性质且序连续的Kothe序列空间.我们只需考虑1＜p＜∞的情况.由引理3，我们选取其中显然xn∈S（cesp）.

下面我们考虑函数f（t）＝1－tp＋（1＋t）p，p≥1：

由于f′（t）＝－ptp－1＋p（1＋t）p－1＝p［（1＋t）p－1－tp－1］≥0，因此f（t）≥f（0）＝2并且 ‖xn－x1‖p≥2，当然有

另一方面，注意到‖en‖→0（n→∞）而且对任意的ε＞0有下式成立：

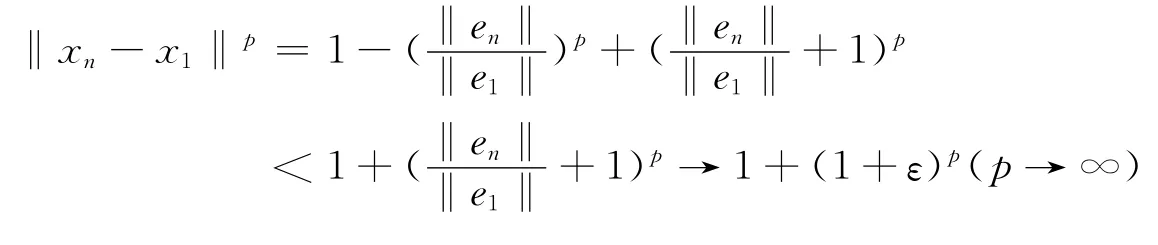
［1］Lee PY.Cesaro sequence spaces，Math.Chronicle，New Zealand 13（1984）29～45

［2］Cui Y A and Hudzik H.On the Banach-Saks and weak Banach-Saks properties of some Banach sequence spaces，Acta Sci.Math.（Szeged）65（1999）179～187

［3］Cui Y A and Hudzik H.Packing constant for Cesaro sequence spaces Nonliner Analysis，TMA 47（2001）2695～2702

［4］J.A.Burlak，R.A.Rankin and A.P.Robertson.The packing of sphere in the space，Proc.Glasgow Math.Assoc.2（1958）22～25

［5］C.A.Kottman.Packing and reflexivity in Banach spaces，Trans.Amer.Math.Soc.150（1970），565～576