基于FCE－DEA－AHP的城市物流绿色度评价研究＊

马金麟 陈 龙

（江苏大学汽车与交通工程学院 镇江 212013）

0 引 言

世界经济的发展给环境带来了严重破坏.作为经济活动的一部分，城市物流系统也面临着环境问题，如污染气体的排放、交通阻塞以及废弃物的不当处理等.于是，世界各国相继把发展绿色物流作为保护环境、爱护自然的关键途径，城市物流产业的绿色度已成为衡量社会发展的和谐程度、城市建设的合理性以及居民生活健康水平的一项重要指标.

由此可见，对城市物流绿色度的比较和评估既有助于找出其发展瓶颈，又可为物流经济的科学发展提供理论指导.

1 城市物流的绿色度评价指标

城市物流的绿色度是城市物流的绿色化程度，而物流的绿色化是指在物流过程中抑制物流对环境造成危害的同时，实现对物流环境的净化，使物流资源得到最充分利用，达到经济效益、社会效益和环境效益的统一.它遵循减量化原则、再利用原则、再循环原则和共存原则［1］.

城市物流的绿色化包括物流作业环节和物流管理全过程的绿色化.从物流作业环节来看，主要包括绿色运输、绿色仓储等［2］.从物流管理过程来看，则是从环境保护和节约资源的目标出发，改进物流体系，既考虑正向物流环节的绿色化，又考虑供应链上的逆向物流体系的绿色化.因此，评价城市物流的绿色度应主要对以下指标进行考量：

1）集约资源 这是绿色物流的本质内容，也是物流业发展的主导思想之一.通过整合现有运力资源、优化资源配置等手段，物流企业可以提高资源利用率，减少浪费.

2）绿色运输 实现绿色运输，首先要对运输线路进行优化，从而缩短运输距离；其次，合理组织货源流向和配载，可减少不合理运输的出现；此外，注重对运输车辆的养护，使用清洁燃料，有益于减少能耗及尾气排放.

3）绿色仓储 绿色仓储有3点要求：第一，仓库选址要合理，便于节约运输成本；第二，仓储布局要科学，实现仓储容积利用最大化，降低单元存货成本；第三，合理配备软硬件设施，提高管理效率.

4）逆向物流 主要通过废旧物品的再利用、再循环和废物处理等手段，实现对环境影响最小化［3］.

2 城市物流的绿色度评价

由于城市物流绿色度评价体系具有递阶层次结构，评价指标涉及诸多因素，且因素信息无法用精确数学语言描述，因此，采用模糊综合评判法、数据包络分析法（DEA）以及层次分析法（AHP）相结合的FDA 集成评价方法对多个城市物流的绿色度进行评价.

FDA 方法的主要思路是：首先用层次分析法确定评价指标体系，使各因素之间的关系层次化、条理化，并能够区分各因素对评价目标的影响程度，然后用模糊综合评判与数据包络分析法计算单因素指标的隶属度，最后结合指标权重对多个评价对象进行综合评价.

2.1 运用AHP确定城市物流绿色度评价体系各指标权重

运用AHP方法，组织专家两两比较指标的相对重要性，给出相应的比例权重，构建上层某要素对下层相关元素的判断矩阵，利用Yaahp 软件，计算判断矩阵的最大特征值及对应特征向量，得出单排序权向量和总排序权向量并分别通过一致性检验［4－5］，计算结果见表1.

表1 城市物流的绿色度评价指标权重汇总表

2.2 运用DEA 与模糊综合评判集成方法评价单因素指标

数据包络分析（DEA）是以“相对效率”概念为基础，根据多指标投入和多指标产出对相同类型的单位（部门）进行相对有效性或效益评价的一种系统分析方法［6］.通常是对一组给定的决策单元（DMU），通过输入和输出数据的综合分析，DEA 可以得出每个DMU 综合效率的数量指标.据此将各决策单元定级排队，确定有效的决策单元，它不仅可对同一类型各决策单元的相对有效性做出评价和排序，而且还可以进一步分析各决策单元非DEA 有效的原因及其改进方向，从而为决策者提供重要的管理决策信息［7－8］.

在DEA 的应用中，最关键步骤就是输入、输出指标体系的确定和各DMU 在相应指标体系下的输入输出数据的搜集与获得.由于城市物流绿色度体系评价因素信息的不确定性，因此提出将模糊集合论与DEA 方法相结合，对各因素指标分别进行评价［9－10］.

2.2.1 模型原理

设W ＝｛w1，w2，…，wk｝为决策单元集，k 为决策单元个数；C＝｛c1，c2，…，cm｝为评价指标集，m 为评价指标个数；P＝｛p1，p2，…，pn｝为评价等级集，n为评价等级个数.

对每一个决策单元，有模糊关系矩阵R，称为某一决策单元的评价矩阵.

式中：rij为C 中评价指标ci对应P 中等级pj的隶属关系.

需要说明的是，评价等级数n 因具体问题及要求不同，取值也不一定.而且具体取哪些等级为DEA 的“输入”和“输出”，评价结果也会有一些差异.对于1个决策单元，它有t种类型的“输入”和s种类型的“输出”，且t＋s＝n.如表2所列.

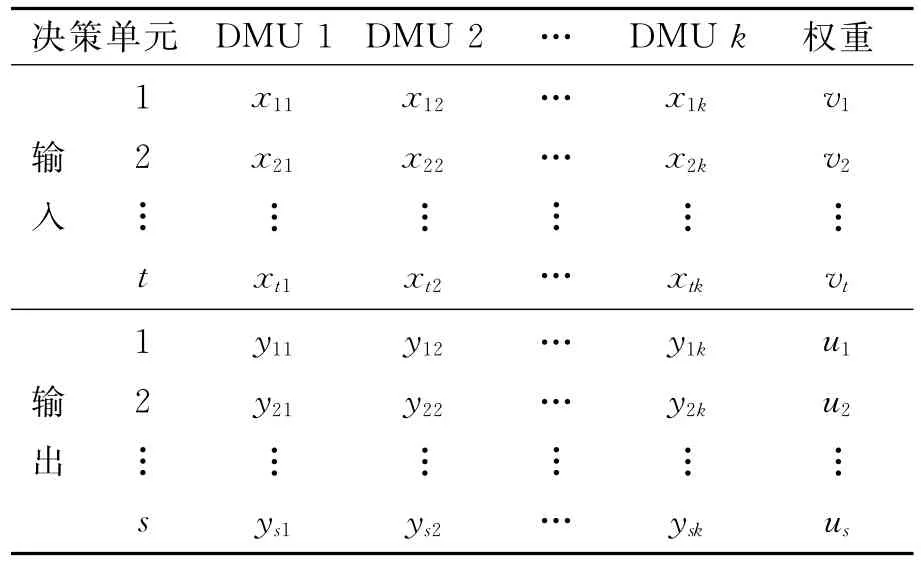
表2 DEA输入、输出表

第j个决策单元的效益评价指数是

式中：Xj＝（x1j，x2j，…，xtj）T，Yj＝（y1j，y2j，…，ysj）T，j＝1，2，…，k，相应的权系数V＝（v1，v2，…，vt）T，U＝（u1，u2，…，us）T.为了便于比较，可适当选取权系数V 和U，使hj≤1.

对于第j0个决策单元进行效率评价，以权U和V 为变量，以第j0个决策单元的效率指数hj0为目标，以所有决策单元（包括第j0个决策单元）的hj≤1 为约束，构成最优化模型（即C2R 模型），化为等价的线性规划问题

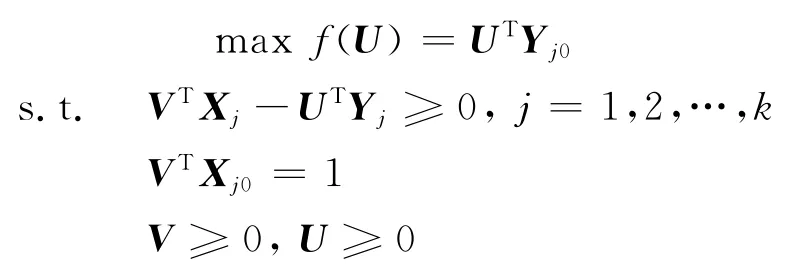
然后用线性规划的最优解来判断决策单元j0的相对有效性.

2.2.2 算 例

以甲、乙、丙、丁4城市的绿色物流开展现状为决策单元，挑选10位专家进行模糊评判（假定各专家的权重相等），评价集P＝｛优，良，中，差｝，统计出该系统的12个因素指标的评价级度，见表3.试评价每个城市在各因素上的表现.

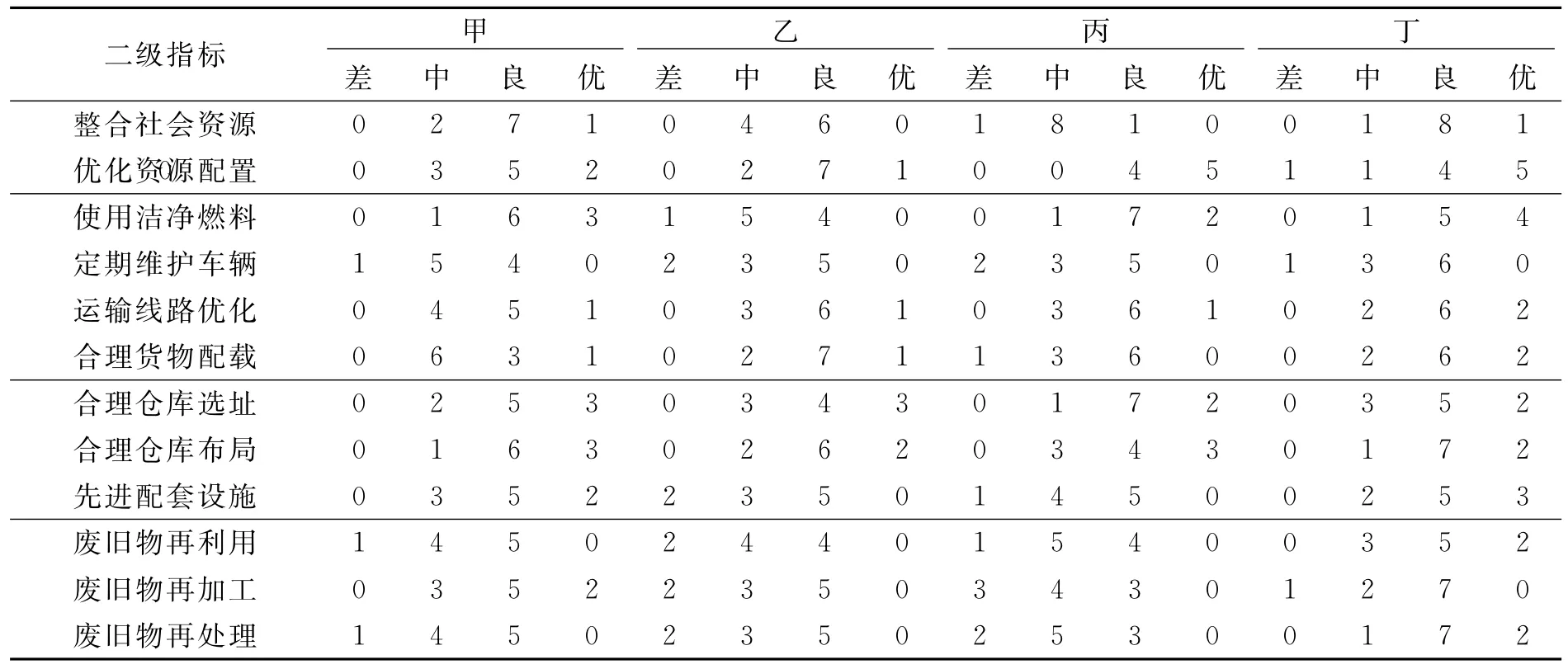
表3 DEA计算基础数据

在利用DEA 与模糊综合评判集成方法计算模糊指标隶属度时，由于DEA 方法要求每个决策单元都应有输入和输出，且每个城市都渴望绿色度较好的物流体系，因此，以“差”（v1）、“中”（v2）为系统的输入，取“良”（u1）、“优”（u2）为系统的输出.

以“整合社会资源”为例，建立线性规划模型.

对于城市甲而言，有Lp1

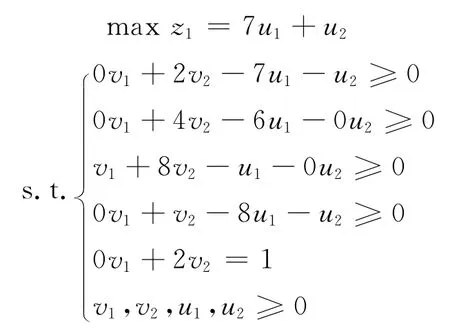
同理，可得其他3个城市的线性规划模型.

采用Lindo软件计算，得到4个线性规划模型的最优目标函数值分别为

城市甲Lp1：max z1＝0.5000

城市乙Lp2：max z2＝0.1875

城市丙Lp3：max z3＝0.0156

城市丁Lp4：max z4＝1.0000

以同样方法可得到甲、乙、丙、丁4个城市在其他因素上的表现，汇总信息见表4.

表4 各城市在每个评价指标上的表现（隶属度）

2.3 城市物流绿色度的综合评价与排序

根据表4中各城市模糊评价指标的隶属度集G＝｛g1，g2，…，gm｝，结合表1各二级评价指标相对于总指标的权重集L＝｛l1，l2，…，lm｝，计算各城市物流绿色度的综合评价得分.由

计算可得：A甲＝0.6744，A乙＝0.6696，A丙＝0.5080，A丁＝0.7492.

因此，4个城市物流绿色度综合评分由低到高排序如下：丙＜乙＜甲＜丁；另外根据表4还可看出，城市甲的物流绿色化在“合理货物配载”和“废旧物再处理”两方面所做的工作比较欠缺，城市乙在“整合社会资源”和“使用洁净燃料”方面有待改进，而城市丙在“整合社会资源”和“废旧物再处理”两方面几乎无所作为，是日后发展的重点，而对城市丁来说，发展的瓶颈则来自于“优化资源配置”和“合理货物配载”.

3 结束语

基于FDA 模型的模糊综合评判方法，由于应用了DEA 的理论，直观性好，通过巧妙构造“输入”、“输出”指标并引入其权重作为模型变量，增强了模糊综合评判结果的客观性.它不仅可以考察城市物流体系在单个因素的绿色度表现，从而发现其优缺点，以便进一步改进和完善，而且由于把多个城市的物流体系放在一起进行讨论和计算，所以可比性强，评价效率高.

［1］刘晓佳，兰培真，郑高哲.可持续发展的综合交通运输系统构成模型研究［J］.武汉理工大学学报：交通科学与工程版，2011，35（1）：122－125.

［2］David C.What the future holds for‘green logistics’［J］.Traffic Engineering and Control，2009，50（5）：215－217.

［3］Sonya H H，Alexander C A，Zhu Zhiwei.Understanding the reverse logistics operations of a retailer：A pilot study［J］.Industrial Management and Data Systems，2009，109（4）：515－531.

［4］杜 栋，庞庆华，吴 炎.现代综合评价方法与案例精选［M］.北京：清华大学出版社，2005.

［5］Aya Zeki，Izadbakhsh H R.A combined fuzzy AHPgoal programming approach to assembly－line selection［J］.Journal of Intelligent and Fuzzy Systems，2007，18（4）：345－362.

［6］Coelli T J，Prasada R D，O′Donnell C J，et al.Introduction to efficiency and productivity analysis［M］.Second Edition.New York：Springer Press，2005.

［7］Hoff A.Second stage DEA：comparison of approaches for modeling the DEA score［J］.European Journal of Operational Research，2007，181（1）：425－435.

［8］Krivonozhko V E，Utkin O B，Safin M M，et al.On some generalization of the DEA models［J］.Journal of the Operational Research Society，2009，60（11）：1518－1527.

［9］Andersen B，Fagerhaug T.Performance measurement of logistics processes［J］.Journal of Operation Management，2003（20）：19－32.

［10］Liu Y M，Luo M K.Fuzzy topology［M］.Singapore：World Scientific，1997.