基于仿真的城市道路交叉口最小安全间距研究

龙雪琴 关宏志

（北京工业大学交通工程北京市重点实验室 北京 100124）

1 道路交叉口安全间距研究理论和评价指标

机动车在城市道路信号交叉口之间的路段上行驶速度和距离的关系如图1所示.其交通流的特性是［6］：由于红灯期间交叉口对车流的挤压作用，车流呈组团行驶状态；同时，由于车辆组团中车辆行驶特性的差别，车辆驶出交叉口后，又具有独特的离散现象.

车辆驶出交叉口后，均处于加速行驶状态，因此车辆速度极不稳定；且各驾驶员驾驶行为特性不同，交通流处于紊乱运行状态，这时车辆之间的车头间距增加.随着驶离交叉口距离的增加，车辆加速到一定程度（路段限速）后速度不再发生变化，并将以此速度稳定运行.此时，虽然车辆速度较大，但是各车辆的速度基本保持稳定，速度变化率降低.稳定运行一定时间后，车辆进入下一个交叉口并减速运行，又进入紊乱运行状态.

图1 车辆驶离交叉口后的运行状态

图1中，S1为车辆驶离上一交叉口后达到稳定状态所需的距离.车辆在“紊乱”运行过程中，车辆之间的速度标准差较大，达到“稳定”运行状态时，速度标准差最小；同时，车辆频繁变化车速将导致事故风险大大提高，因此驶离上一交叉口的车辆应至少在达到稳定行驶状态后再进入下一交叉口，所以交叉口最小安全间距即为车辆达到稳定状态所需的距离S1.

研究表明，速度标准差SD 是影响事故的显著因素，随着速度标准差的增大，事故率上升［7－8］.此外，交通冲突是交通事故的潜在因素，与交通事故有着强烈的正相关性.因此本文选取断面车辆速度标准差SD 和交通冲突数量作为评价安全性的指标.

2 研究方法

Michaels［9］通过分析司机生理和心理一些潜在的因素，首次提出生理－心理跟车模型的理念，通过判断视野中前车尺寸大小的改变，根据感知阈值，判断是否与前车接近，从而选择加减速行为.Wiedemann［10］提出以行为阈值划分跟驰状态，并建立了行为阈值模型，通过判断前后车距，作为选择加减速行为的依据.最符合实际驾驶行为的是Wiedemann建立的MISSION 模型，其跟车行驶阈值见图2.

图2 心理－生理跟驰模型

MISSION 模型中，共有5种行驶状态，每一车间间距和速度差的组合都与一种特定的行驶状态对应.在车辆跟驰过程中，车辆通过调整车速来保持安全间距.当车辆之间间距和速度差位于曲线AX 和横坐标轴所包含的区域内时，车辆处于撞车危险区，此时车辆之间的交互状态为“breakax”；当车辆之间间距和速度差位于曲线BX 和曲线AX 所包含的区域内时，车辆处于制动避祸区，此时车辆之间的交互状态为“breakbx”.当车辆处在这两种交互状态下时，表明车辆之间存在交通冲突.因此本文中以车辆交互状态为“breakax”和“breakbx”的次数作为交通冲突数量，并以此作为判断交通安全性的指标之一.

本文认为驾驶员在路口间的驾驶行为，是在路段条件制约下，受到生理、心理因素的影响的结果.因此，基于图2所示理论曲线，运用仿真软件，研究路口间距和速度标准差SD 的关系.

2.1 实验方法

本文采用VISSIM 微观仿真软件［11］，研究车辆驶出交叉口后在路段上的行驶状态，断面距离以通过行人过街横道为起点.首先标定道路环境和交通流参数，确定影响车辆行驶速度标准差SD 和交通冲突的影响因素，然后进行多次单因素敏感性分析，研究不同实验方案下车辆驶出交叉口后速度标准差SD 和交通冲突数量随断面距离的变化规律，最后通过判断车辆运行状态得到交叉口最小安全间距，并建立影响因素与最小安全间距的函数关系.

红河州充分展示改革开放40年来各族群众的生活巨变 近日，红河州委州政府联合云南广播电视台国际频道，从红河州40周年11个世居民族中精选出11位代表人物，制作《丝路红河》改革开放特别报道。报道采取访谈的形式，分别制作11个专题短片，叙述了红河州11个世居民族在党的十一届三中全会以来的巨大变化。目前，短片正在制作中，并将在改革开放40周年前夕与广大观众见面。

2.2 实验过程

实验假设：交叉口采用信号协调控制；信号控制为四相位；右转采用让行规划.

1）参数标定 车型：小客车和大客车；交叉口处转弯车速：右转15km／h，左转20km／h，直行25km／h；车辆最大加速度3m／s2，最大减速度4m／s2；道路为双向6车道，交叉口处进口车道拓宽，左、右转各1条车道，直行2条车道.

影响因素包括设计速度、交通量、大型车比例、转弯车比例、信号相位周期.为了简化多因素多水平的组合，设定一个典型的主路（本文中主路指所研究的路段所在的道路）交通环境：交通量q＝1200veh／h，大车比例rb＝0.2，转弯比例rt＝0.4（表示左、右转比例之和，且左、右转比例相同）.次要道路交通环境的确定方法：次路交通量和大车比例与主路保持一致；次路转弯比例由主路、次路的交通量和主路转弯比例确定，保证主路上的转入交通量与转出交通量相等.信号周期C由韦伯斯特公式计算得到.

考虑到各项影响因素的评价水平较多，采用多次单因素分析，即保持其他因素水平不变，调节特定因素的水平，考核其变化对结果的影响.仿真方案见表1.

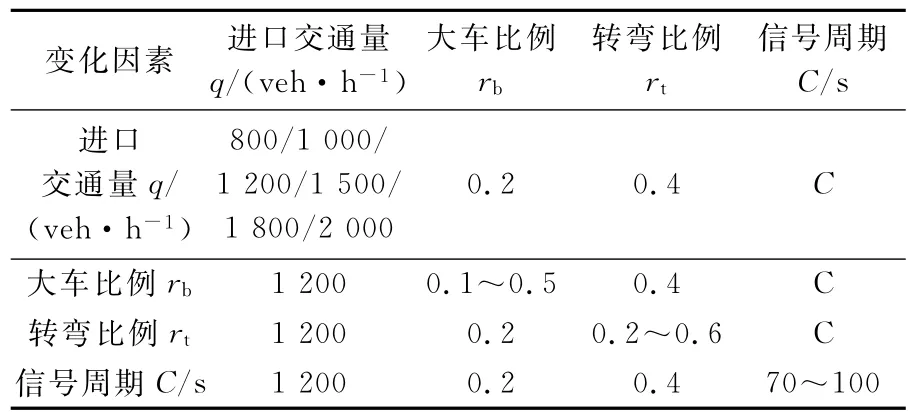
表1 实验仿真方案

每轮仿真通过改变随机数种子的方法做10次实验，将研究的路段每10m 分为一个断面，计算每个断面所有车辆的速度标准差SD 和车辆状态为“breakax”和“breakbx”的次数，然后分别取其平均值，根据速度标准差SD 和交通冲突数量的变化规律判断车辆运行状态.

3 实验结果

3.1 速度标准差

实验结果验证了车队离散理论，当车辆刚驶离交叉口并行驶一段距离后，车辆的速度标准差SD 逐渐减小，行驶距离增大到一定程度后SD 基本保持不变，此时的断面距离即为车辆达到稳定状态所需的最短距离，记为Sv.判断车辆达到稳定状态的标准为：SD 的变化率不超过1%.按照此判断标准，所有实验方案下，车辆达到稳定状态所需行驶的距离Sv总结见表2中①列.实验结论如下.

1）设计速度、交通量、大车比例、转弯比例和信号周期等因素的影响都表现出同样的规律，即随着各影响因素水平的增加，车辆达到稳定状态所需的距离Sv也随之增加.鉴于图例太多，本文只选取了部分图例进行说明.见图3、图4，当限制速度保持不变，交通量等增大时，Sv逐渐增加.而当交通量保持不变，速度增加时，Sv也逐渐增加.

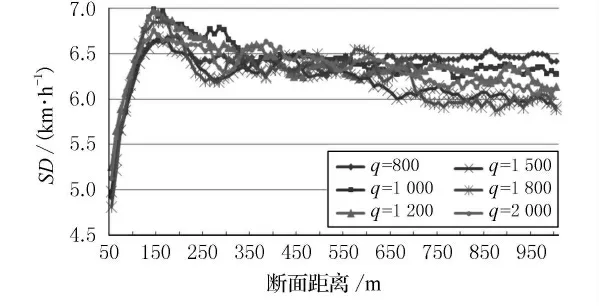
图3 v＝60km／h时交通量变化的影响

图4 v＝50km／h时交通量变化的影响

2）车辆驶离交叉口后，断面车辆SD 先逐渐增大，达到最大值后再逐渐减小直到稳定，且SD增加持续的过程与限制速度有关.如图3所示，当v＝60km／h时，车辆SD 逐渐增大的过程由驶离交叉口持续到断面距离为150m；而图4中，当v＝50km／h 时，SD 增大的过程由驶离交叉口持续到断面距离为120 m 左右.由此可以看出，限制速度v越大，SD 增加过程所持续的距离越长.首先，车辆驶离交叉口后，均处于加速过程，由于车辆加速性能不一，断面上车辆SD 逐渐增加.其次，实验设定的交叉口的速度为15～25km／h，当限制速度越大时，通过交叉口的速度与限制速度差值越大，车辆需要较长的加速过程才能达到限制速度.

3）车辆速度标准差在由最大值下降直到达到稳定的过程中，存在震荡的现象.如图3和图4所示，SD 达到最大后，并不是平滑地逐渐下降.因为在车辆在行驶过程中不断调整速度，因此在车辆之间的速度标准差会产生上下波动现象，但是总体趋势仍然是逐渐下降.

3.2 交通冲突数量

1）车辆状态为“breakax”和“breakbx”次数与驶离交叉口的距离的关系：随着驶离交叉口距离的增加，breakax数量先增加，达到最大值后保持稳定不变，见图5和图6；breakbx数量先增加后减小，呈现二次抛物线的趋势，见图7 和图8.如前所述，车辆驶出交叉口后随即加速，处于紊乱运行状态，在此过程中交通冲突数量也逐渐增加，当车辆加速到限制速度时，交通冲突数量也达到最大.

图5 v＝60km／h时交通量的影响

图6 v＝60km／h时大车比例的影响

2）breakax和breakbx数量与交通量大小和转弯比例有关.如图5和图8所示，同一断面上，交通量大小和转弯比例越大，breakax和breakbx数量也越大；而大车比例和信号周期基本不影响交通冲突数量，在不同的大车比例和信号周期水平下，任一断面上交通冲突数量基本完全相同，如图6和图7所示.

图7 v＝50km／h时交通量的影响

图8 v＝40km／h时转弯比例的影响

从以上分析可以看出，车辆驶离上一交叉口后，交通冲突呈现先增加的趋势，均会达到最大峰值，而达到此最大值后，交通冲突数量均不再增加.breakax和breakbx 数量达到最大值时对应的断面距离分别为Sa，Sb，汇总见表2 中②、③列.从以上分析和图中可以看出，车辆驶过Sa，Sb后，交通冲突数量均不再增加，因此交叉口的间距应至少大于或等于Sa，Sb，因此取Sa，Sb为车辆达到稳定状态所需的距离，即交叉口最小安全间距.

表2 车辆达到稳定状态所需行驶的距离汇总

3.3 回归模型

从上述分析可以看出，车辆达到稳定运行状态所需的行驶距离与限制速度v、交通量q、大车比例rb、转弯比例rt和信号周期C 有关.本文经过60轮仿真实验，得到了不同影响因素水平下，以速度标准差和交通冲突数量作为评价指标判断车辆达到稳定运行状态所需的行驶距离Sv，Sa和Sb.通过回归分析，得到最小安全间距与各影响因素之间的函数关系为

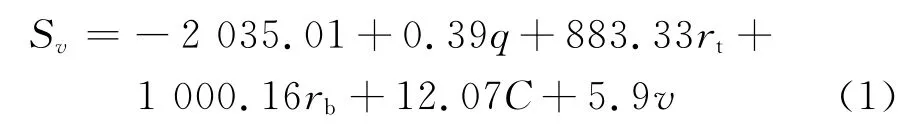
为满足交通安全要求，交叉口最小安全间距应为这3类距离中的最大值，即S1＝max（Sv，Sa，Sb）.在路网规划阶段，通过预测交通量和其组成，结合道路规划和设计的指标，可得到不同限速和交通流状态下道路交叉口之间的最小安全间距.

在路网规划中，路网的结构、间距会受到地形条件、土地利用等很多因素的制约，可能会形成高密度的路网形式，或者在实际路网已经形成的情况下，路网的安全间距无法得到有效保证，交通管理者应该通过设定限制速度保证交通流运行的安全性.根据式（1）～式（3），已知交叉口间距S 的情况下，根据交通流状况和组成，可分别反推出限速值vv，va，vb，最终限速值应取这三者之间的最小值，即v限速＝min（vv，va，vb）.通过减小限制速度值，在交叉口间距保持不变的情况下，仍能保证交通流的安全性，可为城市管理者提供路段限速依据.

4 结束语

本文采用仿真的方法，以车辆驶离交叉口后路段断面上车辆速度标准差和交通冲突数量作为判断指标，研究了不同环境和交通流状态下交叉口最小安全间距；然后建立了交叉口最小安全间距与各类影响因素的函数关系.在路网规划阶段，通过预测交通流状况，结合道路设计指标，可得到不同道路交叉口之间的最小安全间距，同时可应用于城市限速管理.但本文仿真中设定环境较单一，影响因素比较少，建立的模型相对简单，有待进一步完善.

［1］Transportation Research Board National Research Council.Impacts of access management techniques［R］.Washinton，D.C.：National Academy Press，1999.

［2］NAASRA.Guide policy for geometric design of ma－jor urban roads［R］.Australia：National Association of Australian State Road Authorities，1972.

［3］Swedish National Board of Urban Planning.The safety guidelines 1968：principles for urban planning with respect to road safety［R］.1968.

［4］景天然.城市道路条件与交通事故率的关系［J］.同济大学学报，1992（3）：336－340.

［5］张春平，景天然.城市道路交叉口交通安全评价研究［J］.同济大学学报，1994（1）：47－52.

［6］杨佩昆，黄文忠，车丕明.城市道路车队离散过程中的交通流模型［J］.同济大学学报，1994（3）：294－299.

［7］Taylor M C，Lynam D A，Baruya A.The effects of drivers′speed on the frequency of road accidents［R］.TRL Report，No.421.Transport Research Laboratory TRL，Crowthorne，Berkshire 2000.

［8］Garber Nicholas.Speed variance and its influence on accidents［R］.AAA Foudation for Traffic Safety，Washington，D.C.，1988.

［9］Michaels.Perceptual factors in car following［R］.In the Proceedings of the second international symposium on the theory of road and traffic flow，OECD.1963，44：59.

［10］Reiter W.Microscopic traffic simulation：the simulation system MISSION，background and actual State［R］.CEC Project ICARUS（V1052），Final Report，Appendix A，Brussels：CEC，1992.

［11］罗美清，隽志才.VISSIM 在交叉口交通设计与运行分析中的应用［J］.武汉理工大学学报：交通科学与工程版，2004，28（2）：232－235.