基于改进GN 算法的路网脆弱性诊断模型＊

吴俊荻 朱顺应 王 红 刘 兵 丁乃侃

（武汉理工大学交通学院 武汉 430063）

0 引 言

道路网络结构的不尽合理和交通需求分布的过分集中，常导致路网中的部分路段较其他路段容易发生拥堵，从而显著降低网络的通达性，表现出路网的脆弱性.有效识别道路网络的脆弱路段，可帮助道路规划和管理部门预防、监督和管理交通事件的发生.

目前，国内外对路网脆弱性的研究逐渐增多.Husdal［1］认为路网脆弱性是“在某些特定情况下道路运输网络的不可运转性”；而Jenelius［2］Bell［3］和尹洪英［4］认为路网脆弱性的概念包括成2个部分：（1）发生危险事件的概率；（2）在特定地点发生事件的后果.本文中脆弱性的含义与Taylor［5］等定义的类似，即将少量连接的失效（或退化）显著地降低了节点的可达性称为网络节点的脆弱性，将失效的连接称为网络的关键连接.关于路网脆弱性评估方法的研究，Jenelius等假定路网中某些路段失效，把路段失效时广义旅行成本的增加作为评估指标，分析了路段失效的后果.Bell等利用博弈论的方法，预先指定路网的中断或攻击，考虑如何使用混合路径策略使路网期望损失最小化.

这些研究多是针对网络中某些路段失效的特定情况，探究路网功能受到的影响，较少从路网结构和交通需求耦合角度探究脆弱性的产生，本文试图从事这方面的研究，为路网脆弱性问题的改善提供另一视角.

GN 算法是一种通过计算路段介数（网络中所有节点的最短路径经过该路段的次数）识别复杂网络中社团结构的算法［6］，它可以从路网结构角度反映路段的重要程度和发生失效的可能性.目前，该算法已经被应用到了电力系统等领域的连锁故障和脆弱性的研究中［7］.从宏观角度来说，道路网络与其他复杂网络有相似的复杂特征［8］，可借鉴复杂网络的理论来研究它们的结构特征.与其他网络不同的特点是，道路网络的边具有权重和方向性，多数节点的度（与该节点连接的其他节点数目）都小于或等于4.目前还没有研究将GN 算法应用于对道路交通网络进行脆弱性识别的深入研究中.

利用复杂网络理论中GN 算法的思想，结合交通网络的出行需求分布，改进了GN 算法中介数值的计算，然后对路网中的脆弱路段进行识别，并验证该算法应用于道路网络研究中的可行性.

1 模型构建

首先将道路网络中的交叉口和路段分别抽象为网络中的节点和边，与其他复杂网络类似，路网中存在内部节点联系紧密，而对外连接路段较少的组团结构，即路网组团.路网组团之间的连接路段，即是结构性脆弱路段.

本文中，路网脆弱性的含义包括两方面内容.一方面是路网中结构性脆弱路段的分布.另一方面是考虑了交通需求后，路段发生失效的可能性.在确定其结构脆弱性的基础上，将路段的加权介数值（通过某一路段的所有最短路的出行需求之和）与其通行能力比值大于1的路段定义为失效路段，比值越大失效的可能性越大.发生失效说明路段供不应求，容易发生常态拥堵，失去其正常的交通功能.

1.1 模型框架

路网脆弱性识别模型分为两大部分，一是结构性脆弱路段的诊断，二是脆弱路段失效顺序的判断.模型框架见图1.

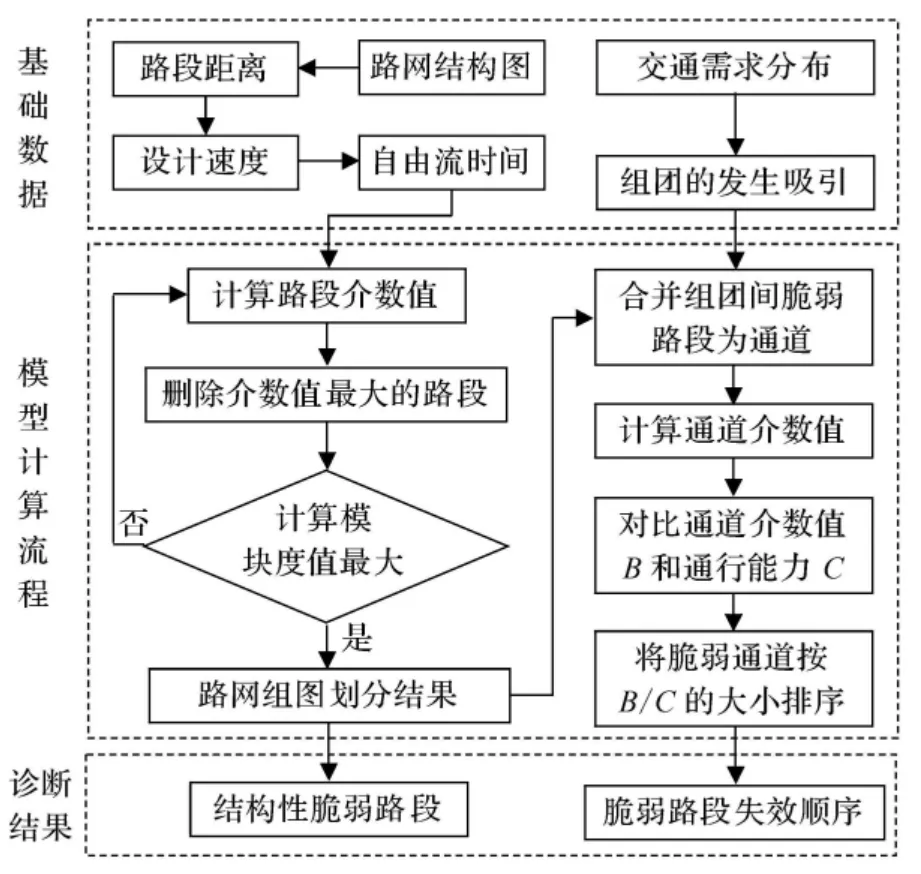
图1 基于GN 算法的路网脆弱性识别模型

1.2 关键方法

为了探究路网自身结构和交通需求分布对路网脆弱性的影响，通过网络介数值反映出用户对路段的选择倾向，从而找出路网中“潜在”的脆弱路段，本模型暂时不考虑交通流的动态变化情况对路网脆弱性的影响，假定用户都试图选择最短路径到达其目的地，并根据同一标准（自由流时间）判断路径长短.

1）介数值计算 首先利用BFS 算法［9］（breadth－first－search）搜索出路网中每一 个节点对的最短路径Dij.

（1）路段介数值bij与原GN 算法中介数值定义类似，路段介数值bij等于每条路段ij 作为最短路段的次数.

（2）OD 加权介数值Bmn考虑了交通需求后改进GN 算法中介数值的计算.在给定路网组团间的OD（发生吸引量）的基础上，将每两个组团间的脆弱路段合并成一条通道，每条通道mn的OD 加权介数值Bmn，等于经过通道mn的所有最短路径出行需求ODxy之和.

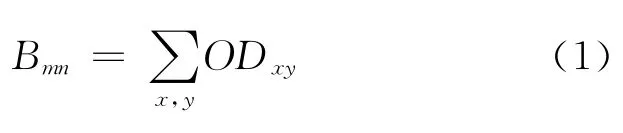
式中：ODxy为OD 对xy 之间的出行需求量.

（3）介数值最大路段的删除 路段的介数值越大，说明通过该路段的潜在交通量可能越大，在网络中的作用越重要，也最容易产生问题.因此，删除介数值最大的路段，相当于模拟该路段交通功能完全失效，路网结构发生变化，从而继续寻找其他易失效的连接路段.计算步骤如下.

步骤1 删除介数值最大的路段max（bij）.

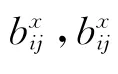
2）路网模块度计算 为确定何时停止删除介数最大路段，Newman等人引进了一个衡量网络划分质量的标准——模块度.每次删除介数值最大的路段之后，都计算一次模块度Q 值，并将每次计算的Q 值绘制成模块度曲线图.他们的研究表明，网络模块度Q 在0到1之间，当Q 等于最大值Qmax时，对应的组团划分能明显体现网络结构问题，且在实际网络中Qmax通常位于0.3到0.7之间.因此，取模块度值达到最大时的组团划分结果作为最后结果.

模块度Q 的计算公式为

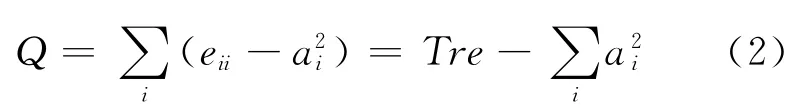
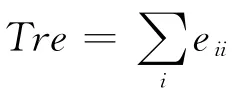
2 案例分析

选取武汉市汉口地区道路网络作为实证研究对象.研究区域的道路网络共有节点140个，路段234条，由4个等级的路段构成：快速路、主干路、次支路、支路，见图2.

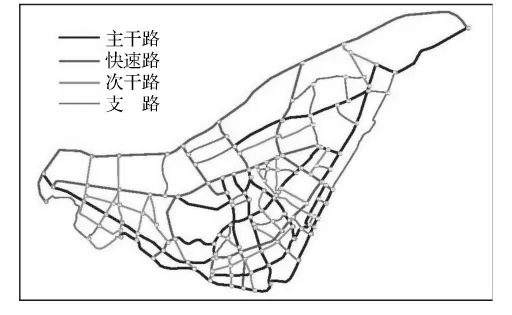
图2 道路网络结构

2.1 结构性脆弱路段

通过编程实现模型计算，得到该路网的模块度曲线变化见图3，模块度的最大值为0.724，此时，对应的组团数目为8个，结构性脆弱路段30条.

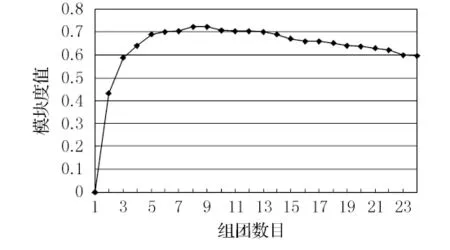
图3 模块度曲线变化情况

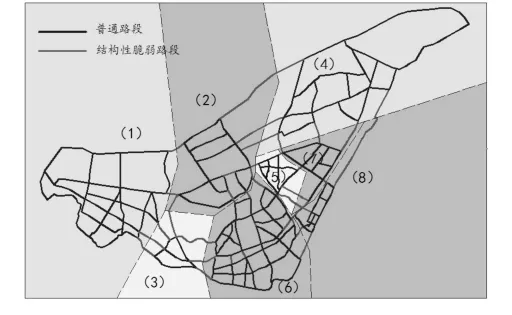
图4 路网结构性脆弱路段及组团划分情况

图4呈现了结构性脆弱路段与路网组团的分布情况.从图中可以看出，与大部分组团内部的路网密度相比，组团之间的连接路段数量很少.其中，组团2－3、组团2－5、组团4－8、组团5－6、组团5－8之间，都仅有一条连接路段.一旦惟一的连接路段失效，组团之间的交通将严重受阻，周围路网和其他组团间的连接路段交通压力将大大增加.这8个组团之间的30条连接路段，是该路网的结构脆弱性所在.要改善该路网结构，提升路网整体通行能力，应从这些结构性脆弱路段入手.

经过统计，案例路网的30条结构性脆弱路段占路网路段总数量的12.8%，其中，有12条主干路、11条快速路、5条次干路和2条支路.

针对以上情况，将结构性脆弱路段分成3类，提出相应的优化措施：（1）高路网密度地区的低等级脆弱路段，分析其日常交通流量，以及周围连接道路的等级，合理提升其道路等级；（2）高路网密度地区的高等级脆弱路段，改善其周围连接道路的通行能力，为该路段分流；（3）低路网密度地区的高等级脆弱路段，提高附近地区的路网密度，修建平行道路，与其共同承担路网组团之间的连通压力.

2.2 脆弱路段失效顺序

路网结构决定了结构性脆弱路段的空间分布，而它们失效的顺序则受交通需求的分布的影响.在组团划分的基础上，把道路网络中的组团简化为其网络质心节点，组团之间的连接路段简化为一条连接质心节点间的通道，可得到如图5所示的简化路网.

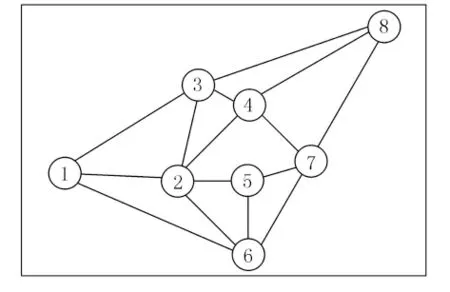
图5 简化路网示意

在已知各组团间发生吸引量ODmn的前提下，通过模型计算得到通道的OD 加权介数值Bmn.通道的通行能力为其合并路段通行能力之和，将介数值与通行能力的比值（B／C）大于1的路段按（B／C）的大小排序见表1.

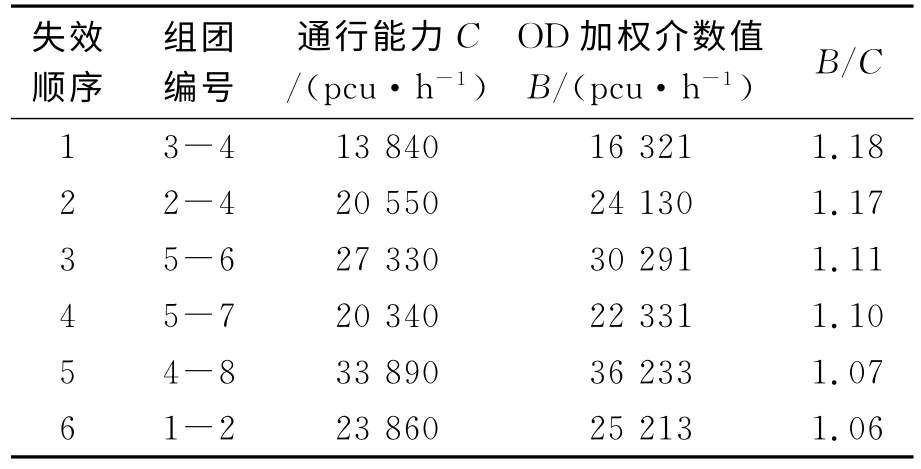
表1 组团间脆弱通道的失效顺序

通道的OD 加权介数值越高，说明这些组团间的交通需求越大；而通道的B／C 比值越大，说明这些连接路段的供给越不能满足组团间的需求，其脆弱性比其他组团间的连接路段更明显.从上表可以看出，连接组团3－4的通道介数值虽然不高，但是其B／C 值最大，说明组团3－4之间的连接路段的需求大于供给，脆弱性最高、最易失效.其次容易失效的路段分别是组团2－4、组团5－6、组团5－7、组团4－8和组团1－2之间的连接路段.

应从增大脆弱路段的通行能力，增加其他组团之间的连接度，以及均衡组团间的交通需求三个方面改善路网的脆弱性.

2.3 模型实用性分析

根据日常观察、交通调查及相关统计资料，可得到当前实际经常发生拥堵路段，为验证改进后GN 算法的准确性，表2对实际拥堵路段与诊断出的部分脆弱路段进行了对比.

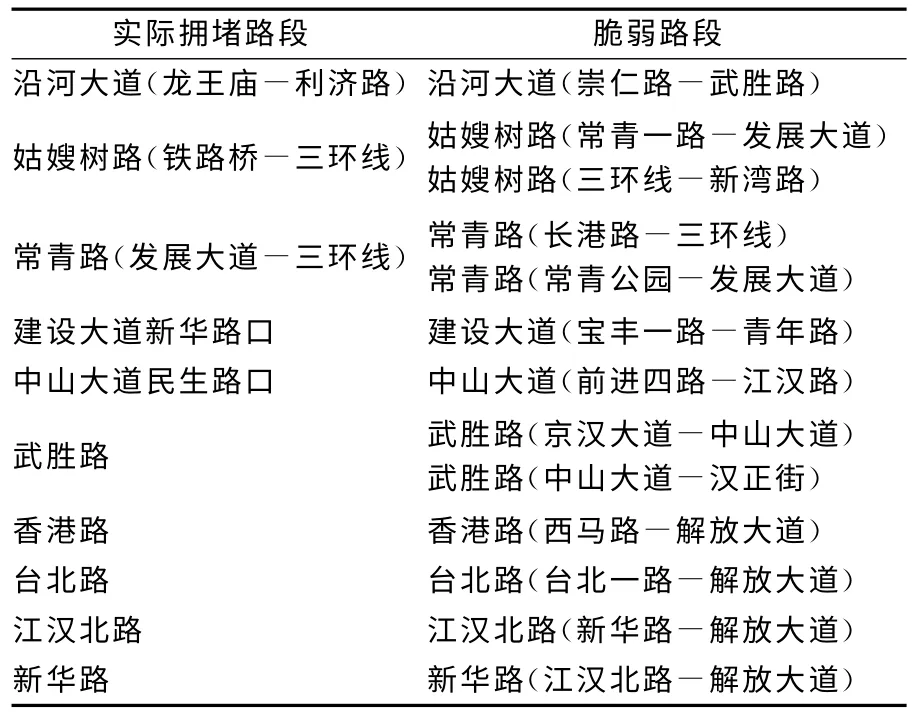
表2 实际拥堵路段与脆弱路段（部分）对比表

尽管模型未考虑交通流和其他因素对用户路径选择的影响，但从上表的对比可以发现，模型诊断出的脆弱路段与实际中发生拥堵的路段匹配度较高.说明路网结构的不合理制约了用户对出行路径的多重选择，使其选择偏好不能完全体现出来，只能选择结构上的最短路.

3 结束语

路网脆弱性的研究在交通运输系统规划、管理过程中具有重要的研究价值.然而，目前对于路网脆弱性的概念界定还很不一致，对脆弱性识别研究的角度也不尽相同.本文从路网结构和交通需求的角度入手，以复杂网络理论的GN 算法为基础，考虑交通需求的权重后对算法中介数值的计算进行改进，构建了路网脆弱性的诊断模型，得到路网的结构性脆弱路段和一定需求分布下脆弱路段的失效情况.对比实际拥堵情况可知，该模型对路网脆弱性的识别具有一定准确性.

与以往研究不同的是，本模型可从路网结构入手对“潜在”的脆弱路段进行判断.可利用本模型对不同类型、不同形态路网的脆弱性进行对比分析，研究结构性脆弱路段的空间分布规律.并可对规划路网设定不同的需求分布，研究其在不同需求下的脆弱性，从而在路段发生失效之前提前采取预防措施.

由于处在研究的初期阶段，模型中最短路的判断标准较为单一，2种介数值的计算方法亦未进行深入的分析评价.未来的研究将进一步探索介数值的计算方法及其合理性，进而全面研究路网脆弱性的影响因素、动态变化及优化措施.

［1］HUSDAL J.Reliability and vulnerability versus cost and benefits［C］／／Queenstown and Christchurch，New Zealand，The 2nd International Symposium on Transportation Network Reliability，2004：180－186.

［2］JENELIUS E.Network structure and travel patterns：Explaining the geographical disparities of road network vulnerability［J］.Journal of Transport Geography，2009（17）：234－244.

［3］BELL M G H，KANTURSKA U，SCHM＾ECKER J D，et al.Attacker－defender models and road network vulnerability［J］.Philosophical Transactions of the Royal Society A－Mathematical Physical and Engineering Sciences，2008，366（1872）：1893－1906.

［4］尹洪英，徐丽群.道路交通网络脆弱性评估研究现状与展望［J］.交通运输系统工程与信息，2010，10（3）：7－13.

［5］TAYLOR M，SEKHAR S，D′ESTE G.Application of accessibility based methods for vulnerability analysis of strategic road networks ［J］.Networks and Spatial Economics，2006（6）：267－291.

［6］NEWMAN M E J，GIRVAN M.Finding and evaluating community structure in networks［J］.Phys.Rev.E，2004，69：113－126.

［7］徐 林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别中的应用［J］.中国电机工程学报，2010，30（1）：33－39.

［8］LAMMER S，GEHLSEN B，HELBING D.Scaling laws in the spatial structure of urban road networks［J］.Physica A，2006，363：89－95.

［9］AWERBUCH B G.Distributed BFS algorithms［J］.Foundations of Computer Science，1985（10）：250－256.