用ANSYS分析边坡稳定性

高恭星

（重庆大学土木工程学院，重庆400030）

0 引言

边坡的稳定性可以用安全系数K来表示。K>1,边坡稳定；K=1，为临界状态；K<1，边坡失稳。

目前，在工程中计算边坡的稳定性的方法主要是建立在极限平衡理论的基础上如Janbu法、瑞典条分法、Bishop法等。在计算安全系数时需要假设滑动面的形状。而用有限元法分析，考虑材料的属性，应力应变的关系，满足力的平衡，不用做任何假设，计算完成后不仅能得到比较准确的安全系数，而且还能得到破坏时的滑移面，塑性应变区域、应力场、位移场等结果。用有限元法分析边坡，可以考虑复杂土层介质，边坡内部的介质的应力应变，分析各种形状的边坡。在得出安全系数的同时还可以清楚认识边坡滑移的类型，这对边坡加固工程具有指导性作用。

用有限元分析边坡的稳定性一般采用强度折减法。本文基于强度折减法理论，运用ANSYS分析边坡的稳定性。

1 有限元强度折减法的原理

有限元强度折减法的原理就是将岩土体的抗剪强度指标减小为c/K，tamφ/K， 把经计算出的c'和φ'代替原来的c和φ，重新代入有限元中进行计算，反复迭代。当岩土体达到极限平衡时，有限元计算不收敛，边坡破坏。此时对应的折减系数K为边坡的稳定安全系数[1]。

2 边坡失稳判据

在有限元计算中，不断增大K值，降低坡体的稳定性，直到边坡破坏。判断边坡是否失稳，主要有以下几种判据：（1）有限元计算是否收敛：在有限元迭代计算中，当计算不收敛时，认为边坡破坏。（2）塑性区是否贯通：在有限元计算中不断增大K值，可以得到边坡塑性应变的应力云图，当塑性区从坡底到坡顶贯通时，认为边坡破坏。（3）位移突变：在分析中当边坡的滑动面和位移发生突变且无限发展，认为边坡破坏[2]。

上述三种判据的（1）、（3）在有限元计算中不收敛，这两种判据是一致的，坡体的塑性区贯通是边坡破坏的必要条件，但是并不一定会发生失稳，边坡的滑体出现无限位移或突变位移，才是边坡破坏的标志。而此时有限元计算也不收敛。所以在ANSYS分析边坡稳定性时判断边坡是否失稳应该以计算不收敛、坡体位移发生突变且无限发展作为基本判据，并结合边坡的塑性区从坡底到坡顶是否贯通来考虑。

3 屈服准则

分析时坡体的材料本构模型采用理想弹塑性模型。目前，ANSYS分析岩土工程主要采用Drucker-Prager（简称DP）屈服准则，是摩尔-库伦准则的近似，通常称为DP准则或广义密塞斯准则，是以密塞斯准则为基础，但是考虑了主应力对土体的抗剪强度[3]。

DP屈服准则可表示为：

材料常数β和屈服强度σy的表达式如下：

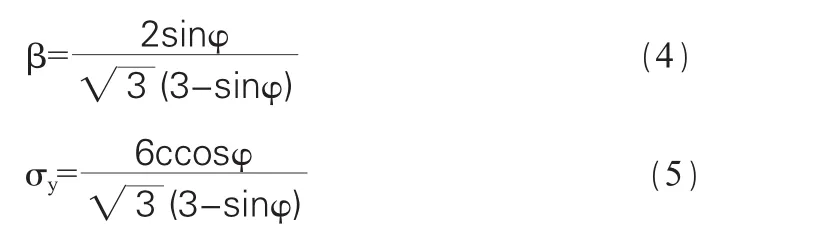
式中，φ为岩土体的内摩擦角；c为岩土体的黏聚力。

表1为通过其他近似的方式得到了不同准则，以修正ANSYS中的DP准则。在ANSYS中只能使用DP准则，如果要使用其他修正准则，则需要利用DP准则的β和σy与其他修正准则的β和σy相等这一条件，反算出φ和c才能把其他准则运用到ANSYS中。

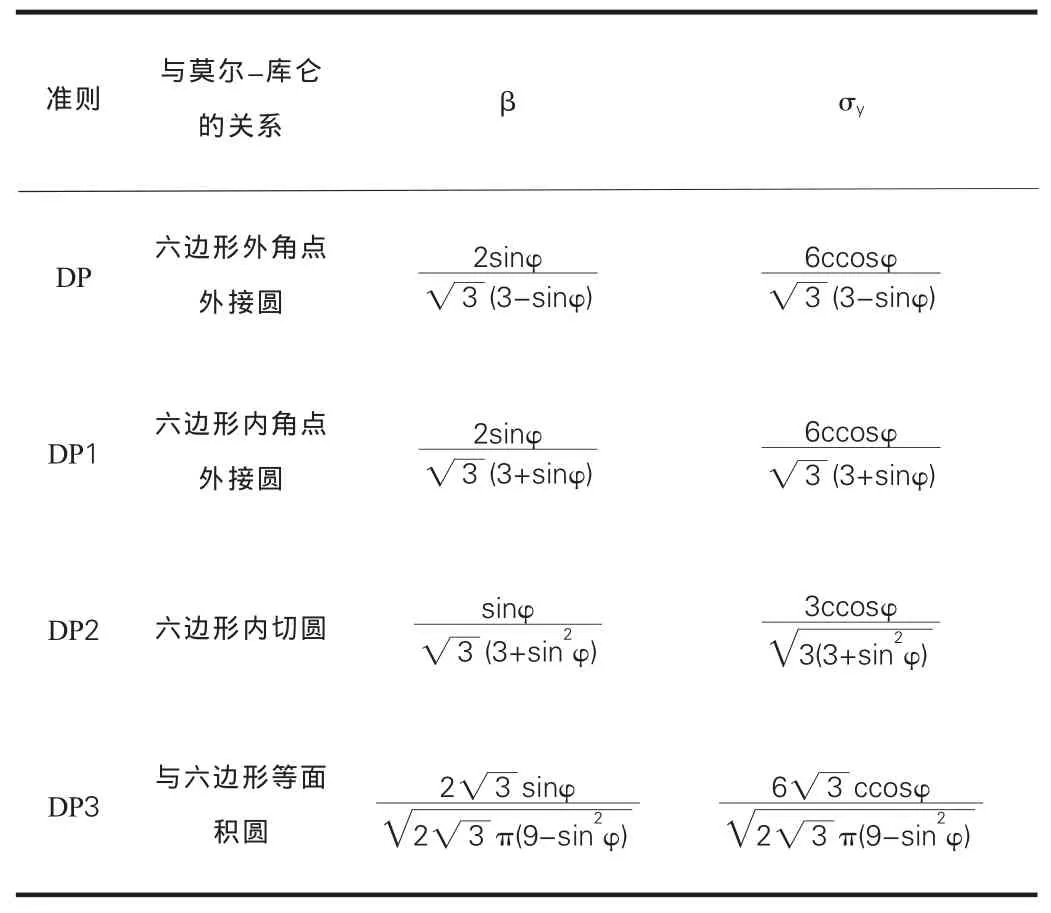
表1 各准则参数计算

在岩土工程中常用的DP准则有DP1六边形内角点外接圆和DP3与六边形等面积圆。在实际运用中DP准则的平均误差较大，DP1准则在计算中存在较大的离散度，而DP3的误差小而且离散性也不大[4]。所以用ANSYS分析边坡稳定性时应该采用DP3准则。

假设边坡的内摩擦角为φ3，粘聚力为c3，采用DP3准则时要转化φ3和c3，利用DP和DP3准则的β和σy相等，计算出在DP准则下的φ和c。经计算可得：

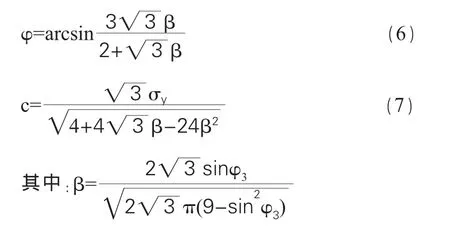
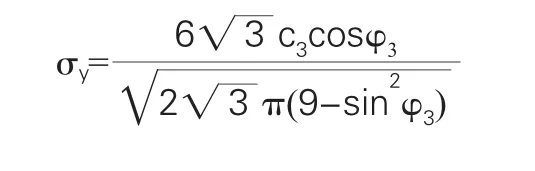
4 有限元模型的建立

屈服准则的选用会影响安全系数的大小，此外所建立的有限元模型对安全系数也有很大影响。在有限元计算中，模型对边界条件很敏感，当坡脚到最近的水平边界的距离不小于边坡高度的1.5倍距离，坡顶到最近的水平边界距离不小于边坡高度的2.5倍距离，并且上下边界总高度大于2倍边坡高度时，计算的安全系数比较合理[5]。网格划分时要考虑合理的网格密度，本文建立的有限元模型尺寸如图1。网格划分如图2。

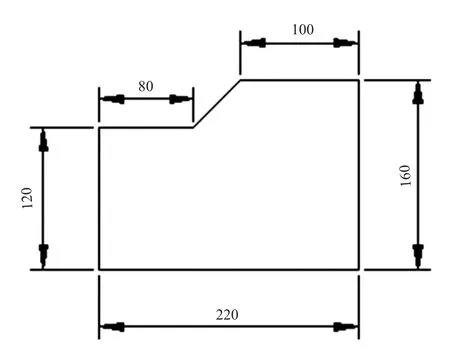
图1 模型尺寸

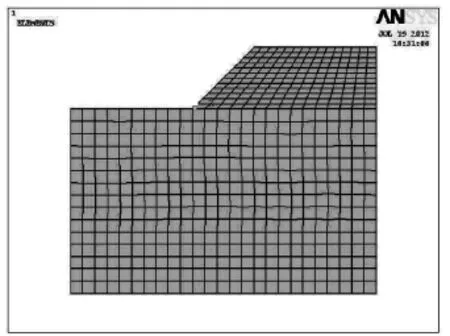
图2 模型网格划分

5 算例分析

边坡物理力学参数取值：内摩擦角φ=20°，黏聚力c=45kPa，重度γ=22kN·m-3，弹性模量E=200MPa，泊松比μ=0.25

边界条件为底边X、Y方向约束，左右为X方向约束。

在重力作用下,边坡的强度折减系数从1.0开始不断增大,在ANSYS中不停地迭代，计算出边坡破坏时的强度折减系数。

直接采用DP准则时：内摩擦角φ=20°，黏聚力c=45kPa。

图3 K=1.20塑形应变云图

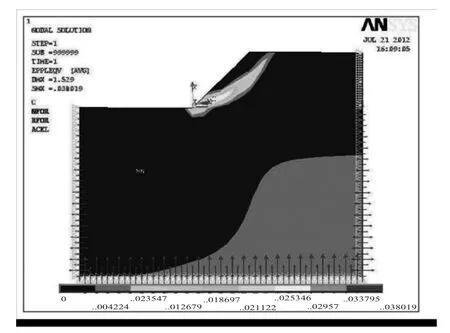
图4 K=1.22塑形应变云图

从边坡模型的数值模拟图可得出,随着强度折减系数K的增加,塑性区逐渐发展,强度折减系数K=1.2的云图可看出塑性区在不断发展，当K=1.22时,ANSYS计算不收敛,根据边坡失稳的判据可得此时边坡已经破坏。边坡的稳定安全系数为1.22。

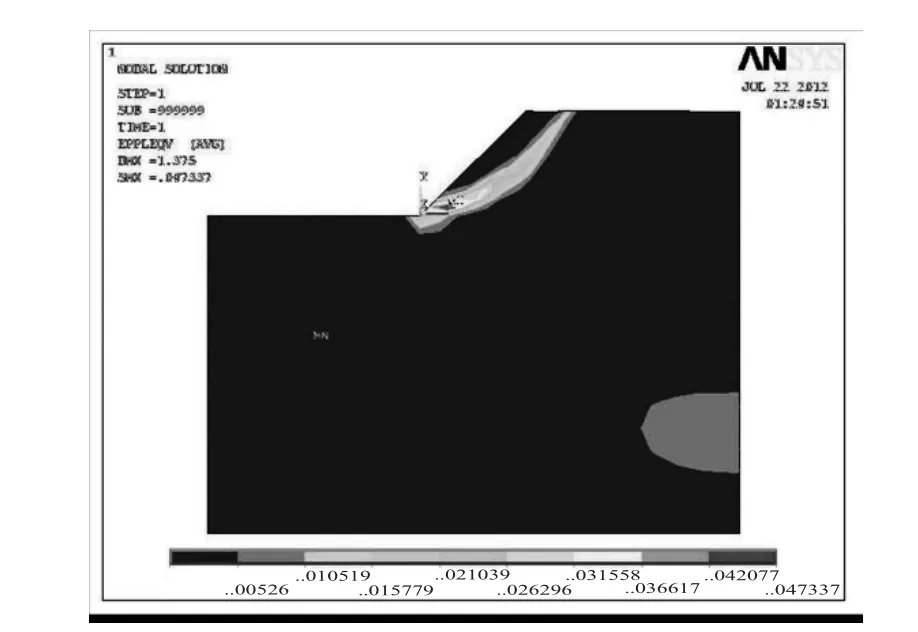
图5 K=1塑性应变云图

采用修正DP3准则时：内摩擦角φ=20°，黏聚力c=45kPa，运用公式(6)和（7）转化φ和c值得：

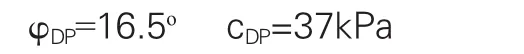
采用DP3准侧当边坡强度折减系数K=1时，ANSYS计算不收敛，且塑性区从坡底到坡顶贯通，边坡失稳，边坡的安全系数为1。

6 土体c、φ对边坡安全系数的影响

土体的内摩擦角和粘聚力是影响安全系数最直接的两个参数，参数的选取对安全系数的计算有很大的影响。下面结合理正软件和ANSYS分析这两个参数对边坡安全系数的影响。

从图6可以看出，粘聚力c不变时，当内摩擦角φ从5°增大到25°时，用三种方法计算出的安全系数K也逐渐增大。K和φ的关系曲线近似一条直线，这三条线的斜率比较大,这说明内摩擦角对安全系数K影响较大。从表2可得出，用瑞典条分法计算出的安全系数与用ANSYS计算出的安全系数相比较，差值百分比在9%～14.5%之间，Janbu法和ANSYS相比较，计算出的安全系数差值百分比在4%～10.9%之间。

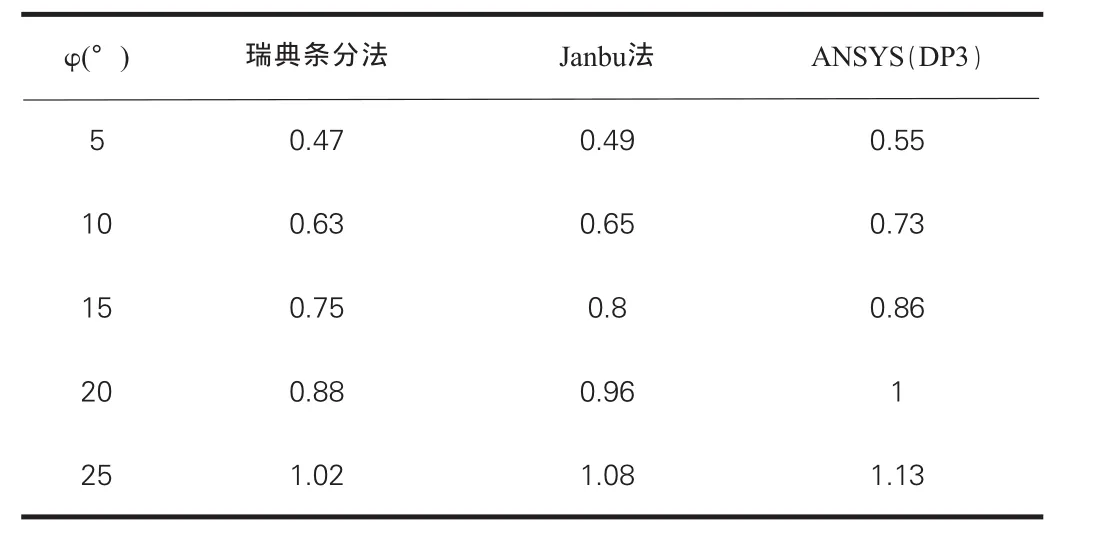
表2 安全系数K与φ的关系

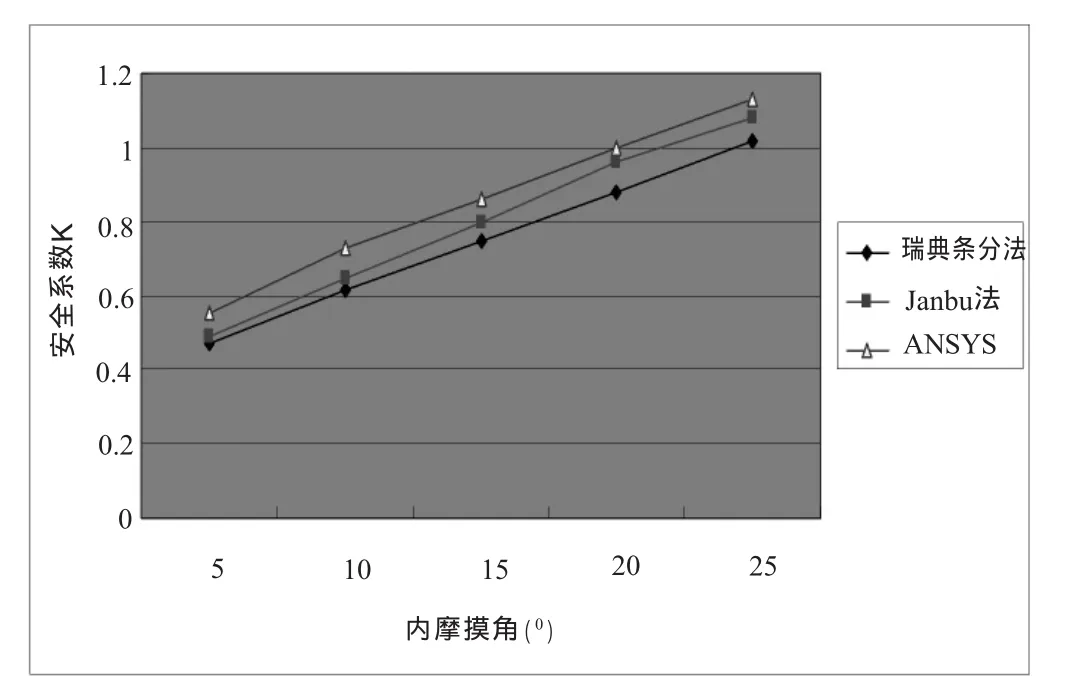
图6 安全系数K与φ的关系

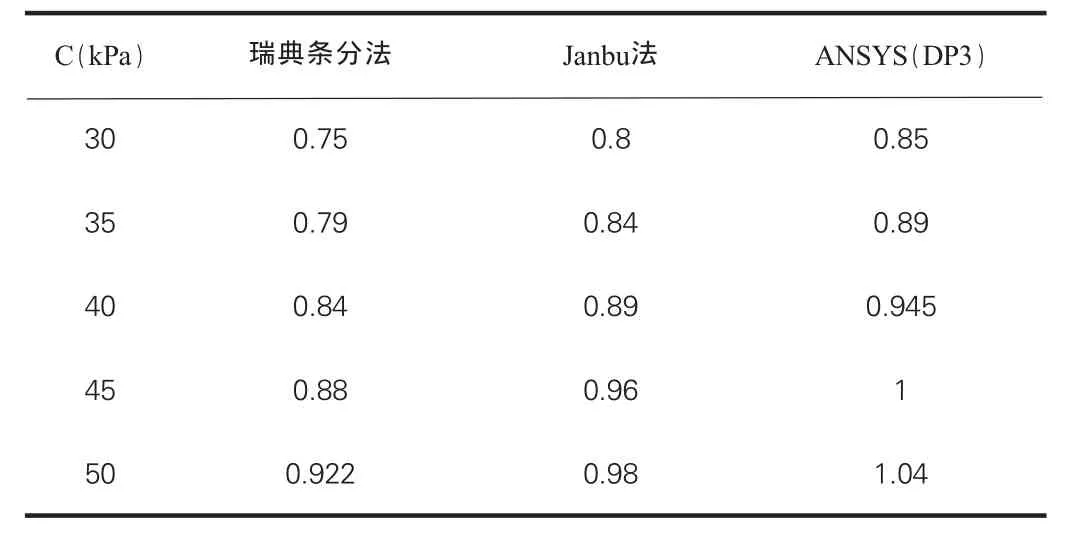
表3 安全系数k与c的关系

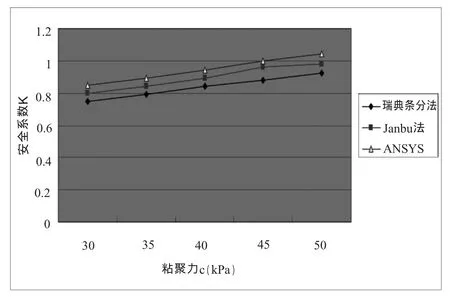
图7 安全系数K与c的关系

从图7可以看出，内摩擦角φ不变时，当粘聚力c从30kPa增大到50kPa时，用计算得出的安全系数K也逐渐增大，但是增长趋势较平缓，这说明粘聚力c对安全系数K有影响，但影响不是很显著。从表3可得出，瑞典条分法和ANSYS相比较，计算出的安全系数，差值百分比在11.1%～12%之间；Janbu法和ANSYS比较，计算出的安全系数，差值百分比在4%～5.8%之间。

由图6和图7分析可得出，在计算边坡稳定性时，c和φ对边坡稳定性都有影响，但是内摩擦角φ的变化对安全系数的影响比较大，而粘聚力c的变化对安全系数的影响比较小。由表2和表3的数据分析可得出，用瑞典条分法计算出的安全系数和ANSYS计算出的安全系数差别比较大，最大差值百分比达到14.5%，而Janbu法和ANSYS计算出的安全系数差值百分比最大仅为10.9%。产生差别的原因有以下几点：

（1）瑞典条分法忽略了土条之间的相互作用力的影响，还假定各土条为刚性不变体。（2）Janbu法假定了滑体中的推力线已知，假定土条两侧的作用力作用在距土条底部1/3高度以上。由于瑞典条分法没有考虑土体间的相互作用力，所以计算得出的安全系数比较小。而Janbu法考虑了土体之间的作用力，所以Janbu法和ANSYS计算出的安全系数差别较小。

7 结论

通过以上分析可得出下列结论：

(1)用ANSYS分析边坡稳定性时，用DP3准则比用DP准则误差小。实际应用时应采用修正的DP3准则，计算出的安全系数更接近实际情况。

(2)用ANSYS分析边坡稳定性与传统分析方法相比较，有一定的差别，但是差别不是太大，可以应用到实际工程中。

(3)内摩擦角φ和粘聚力c对安全系数都有影响，其中内摩擦角φ对安全系数的影响更明显。因此在计算边坡稳定性时要合理考虑φ的取值。

(4)用ANSYS分析边坡稳定性，计算出的安全系数比传统方法计算出的安全系数大，主要是由于ANSYS分析考虑了土体之间的相互作用力。

[1]郑颖人，赵尚毅.用有限元强度折减法进行边坡稳定分析[J].中国工程科学，2002,4（10）：343-346.

[2]赵尚毅，郑颖人.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002,34（3）：57-61.

[3]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007：494-495.

[4]柳林超，梁波.基于ANSYS的有限元强度折减法求边坡安全系数[J].重庆交通大学学报，2009,28（5）：900-901.

[5]郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报：2004,23（19）：3381-3388.