三峡库区堆积层滑坡变形破坏演变机理
唐晓松郑颖人谭万鹏
(1后勤工程学院军事建筑工程系,重庆400041;2重庆市地质灾害防治工程技术研究中心,重庆400041)
0 引言
滑坡演化机理旨在滑坡各种诱发因素作用下,显示滑坡的发生、变形、破坏的全过程与时空规律,包括滑动的原因、运动的特点以及滑动演化的时空过程,从广义上说,还应包括滑坡的预报。
滑坡演变机理与工程地质因素有关,因而各种滑坡的成因不同、机理不同,例如三峡库区滑坡主要为基岩上的岩土堆积层滑坡,滑面就是基岩面,动因主要是重力与库水升降作用。
当前人们对滑坡演变机理一般是从宏观观察的角度上加以定性描述,依据滑坡的变形量大小,把滑坡分为弱变形阶段、强变形阶段和临滑阶段。随着监测仪器的发展,监测滑坡的各种力学变量,尤其是位移监测获得了广泛应用。由此可依据监测的位移数据,应用位移速度来描述滑坡的发展过程,斋藤把滑坡分为减速蠕变阶段、等速蠕变阶段和加速蠕变阶段。尽管人们获得的是定量的位移与位移速度数据,但由于没有把这些数据与滑坡演变过程紧密联系起来,仍然不知道滑面的受力与发展过程、滑坡稳定安全系数降低的演变过程,也无法预测滑坡发生的时刻。因此急需提高并深化人们对滑坡演变机理的认识,尤其是需要从定性认识走向定量认识,从模糊抽象认识走向可视的具体认识。当前力学理论和计算技术的发展,使这种认识的提升成为可能。本文就是应用新近发展起来的数值极限分析方法(包括有限元强度折减法和超载法)[1-2],或称有限元极限分析方法[3-4],并应用国际上通用的软件来提升这一认识。这种方法原理十分简单,是通过不断降低岩土强度和进行弹塑性数值计算,直至破坏,自动生成破坏面,并发生破坏信息。到破坏时的强度降低系数就是滑坡的稳定安全系数,其结果与传统方法求得的稳定安全系数完全一样。该方法不仅能求滑坡的稳定安全系数,还能求出滑面的位置、形态与发展过程[3-4],十分适用于滑坡演化机理的描述。
文章针对堆积层滑坡的变形破坏演变机理,采用了数值分析定量计算的方法,通过与监测数据的对比分析,来显示滑面的发生、受力与演变过程;获得监测点的监测位移速度与不同稳定安全系数下的计算位移速度,以及监测位移-时间曲线与不同稳定安全系数下计算位移-时间曲线,由此可反映不同的滑坡发展阶段;并通过计算位移-时间曲线与监测位移-时间曲线的对比,确定不同时刻的滑坡的实时稳定安全系数;由此可以定量区分滑坡的各个阶段,获得滑坡的临滑时间及预测最终滑动时间,为滑坡的预报预警提供可靠依据,这就是本文要做的工作。
1 采用多手段、分阶段分析滑坡蠕变破坏的演化过程[5]
人们对滑坡蠕变破坏演变过程的认识,一般基于三种手段:一是通过宏观现象的直接观测;二是通过监测数据的分析;三是通过对滑坡稳定的定量力学分析。目前主要还是应用前两种手段,获得的认识是定性的和模糊抽象的,仍需要通过先进的力学手段和计算手段,加强第三种分析手段,以获得定量的、具体可视的机理认识,下面对三种分析方法加以简要阐述。
1.1 滑坡蠕变破坏的宏观现象的观测分析
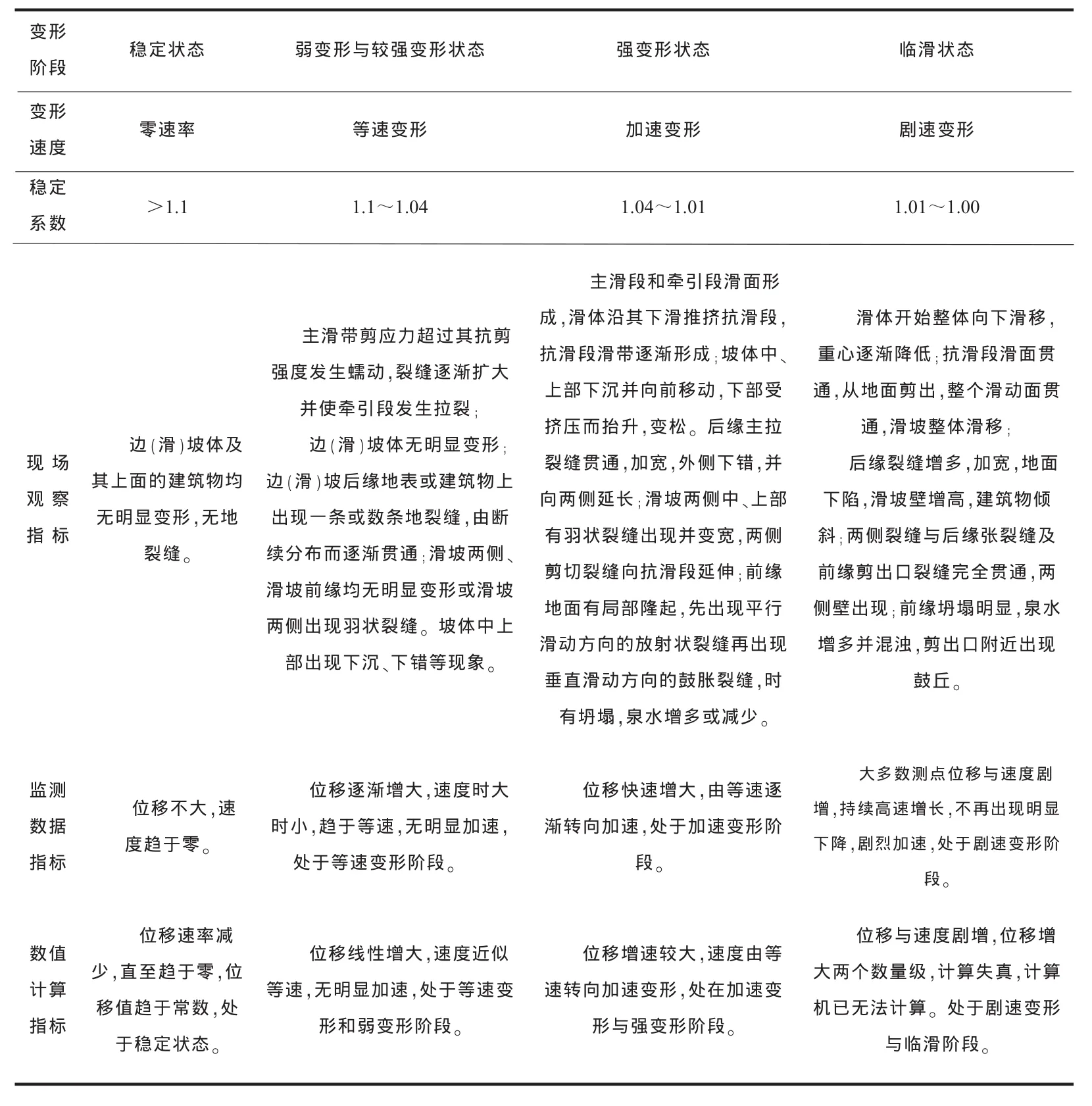
表1 滑坡蠕变破坏演化过程的阶段划分与评价指标
由于人们长期以来都采用这一手段分析滑坡机制,目前已积累了较多经验[6],但这种认识仍然是经验性的、模糊抽象的,不确定性很大,单凭这一认识不能认清滑坡蠕变破坏的机制。在这一认识基础上,可把滑坡的全过程分为稳定、弱变形、强变形和临滑四个阶段,表1从现场观测、监测数据、数值计算三方面给出了滑坡阶段的划分及其相应的评价指标。
1.2 滑坡蠕变破坏的监测位移分析
随着监测仪器的发展,滑坡的位移监测日益普及,这些数据为滑坡演变机制的研究提供了新的分析手段。监测数据表明,随着滑坡变形的发展,位移速度逐渐增大,斋藤据此提出了滑坡蠕变的三个阶段:减速蠕变阶段、等速蠕变阶段和加速蠕变阶段[7-8],可以作为划分滑坡阶段的依据,但从实用方便起见还可将第三阶段分为:加速蠕变段与剧速蠕变段,从而形成减速蠕变阶段、等速蠕变阶段、加速蠕变阶段与剧速蠕变阶段四个阶段。其中,加速蠕变阶段表示滑坡将加速发展,剧速蠕变阶段表示进入临滑状态,即将发生滑坡。上述四个阶段可以简化为变形速度为零、等速、加速、剧速四个阶段,由此与稳定、弱变形、强变形和临滑四个阶段相对应。
图1所描述的是典型的、具有普遍意义的滑坡位移-时间曲线,图1中A点表示等速蠕变和加速蠕变的临界点、B点表示加速蠕变过渡段和剧速蠕变的临界点。但在实际工程中,不同成因类型的滑坡,其位移-时间曲线可能会有所差别,尤其是受各方面条件的限制(如监测周期、监测精度等),或滑坡在其发展演化过程中遭受不同类型外界因素的影响,使得滑坡位移-时间曲线变得更加复杂。监测数据分析的滑坡蠕变破坏演化过程的阶段划分与评价指标见表1。
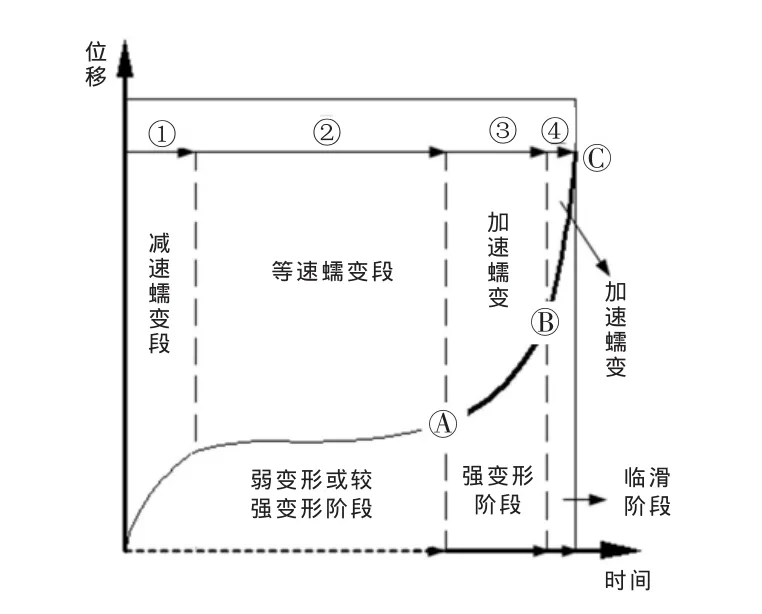
图1 滑坡蠕变四阶段的划分
通过对三峡库区大量滑坡监测资料进行归纳总结可以发现,对于三峡库区内大量存在的堆积体滑坡而言,其滑坡位移-时间曲线大致有曲线型(图2a)和阶梯型(图2b)两类。由于下雨、库区水位升降等原因,对于下部地形较平缓的滑坡,一般产生均匀向前滑动,出现曲线型位移-时间曲线;而对于下部地形较陡和易受库水水位波动影响的滑坡,一般出现台阶形位移-时间曲线。
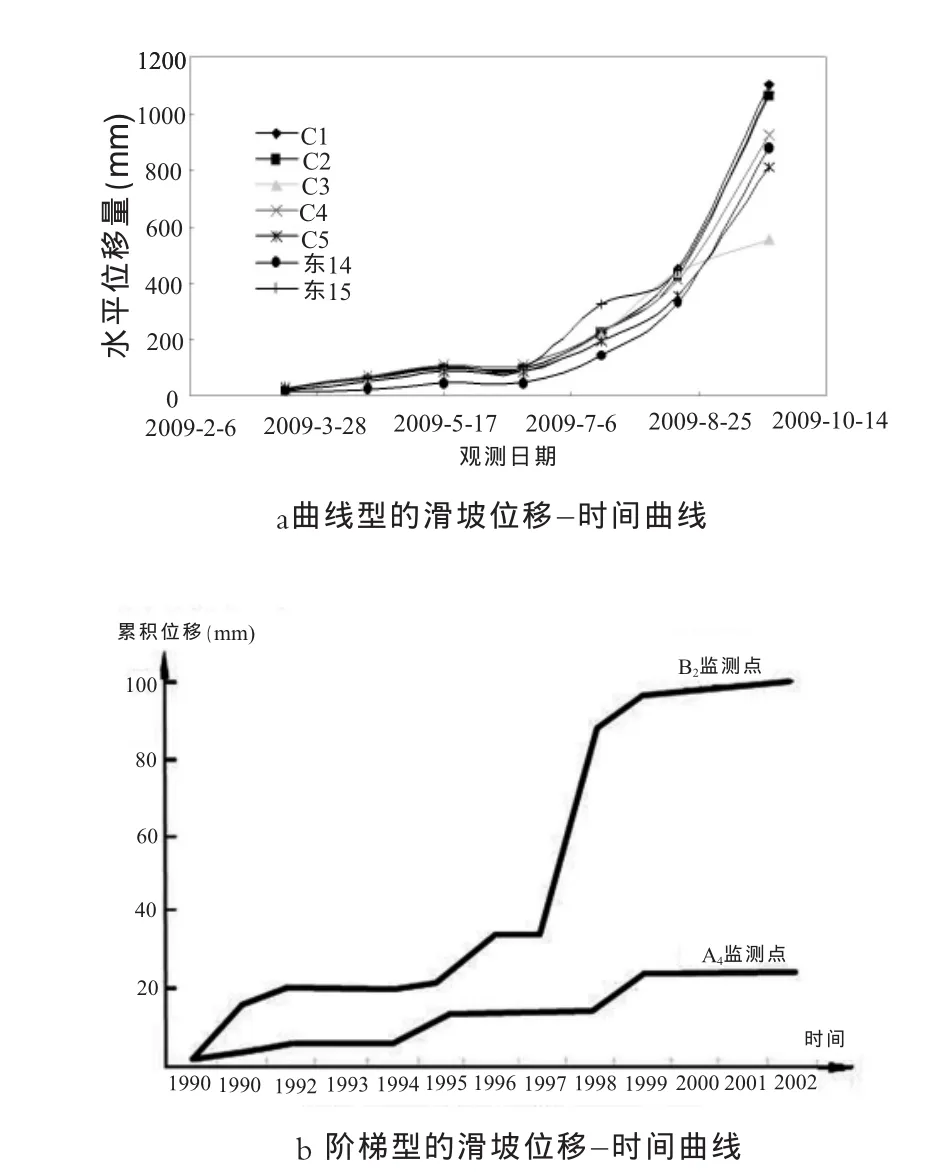
图2 堆积体滑坡位移-时间曲线
2 滑坡蠕变破坏与稳定性的定量分析
上述两种分析方法,只能定性地确定滑坡的演化过程,更重要的是要定量地确定滑坡的演化过程:包括监测点的位移-时间曲线,滑面的受力、变形、破坏的演化过程,滑坡稳定安全系数的降低过程,以及滑坡的预警预报过程。这里采用数值计算的方法对松散堆积体滑坡的变形破坏演变机理进行研究。
2.1 监测点位移-时间曲线的计算
监测点位移-时间曲线除了可用测量获得,也可通过黏弹塑性模型计算确定。本文选用FLAC3d软件中Cvisc模型进行计算,其一维应力状态下的蠕变模型如图3所示。
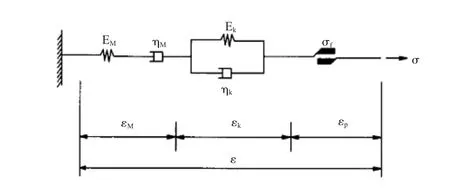
图3 FLAC3d中Cvisc蠕变模型示意图
该模型由马克斯韦尔模型、开尔文模型(两个模型串连成为Burger模型)和一个塑性元件串连而成。图3中,σ为岩土体应力,Em、Ek、ηm和ηk分别为弹性模量、粘弹性模量、马克斯韦尔粘滞系数和开尔文粘滞系数,σf为岩土体材料的屈服强度,εm、εk和εp分别为马克斯韦尔体、开尔文体的应变和塑性应变。如果将ηm取为零,而开尔文体的参数不为零时,Cvisc模型将退化为广义开尔文模型和摩尔-库仑塑性元件的串联。为简便起见,本文在位移-时间曲线的计算中采用的是上述模型。图4列出了不同稳定安全系数条件下的滑坡位移-时间曲线,从图中可以看出,随着时间的增加,位移不断增加,而且曲线的变化还与滑坡的稳定安全系数有关。稳定安全系数越小,位移-时间曲线越陡,表明稳定安全系数小时,位移迅速增加。
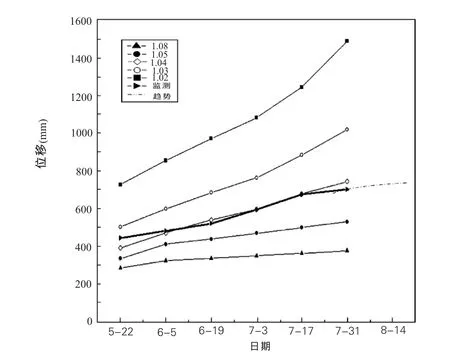
图4 数值计算位移趋势曲线与监测位移关系曲线
滑坡的稳定安全系数与滑面的强度有关,滑面强度越低,滑坡稳定安全系数越小。滑坡的稳定安全系数可采用粘弹塑性有限元强度折减法计算[9-10],也可采用弹塑性有限元强度折减法计算[3],两者结果一致,这主要是因为稳定安全系数与变形无关。随着滑面强度的降低,即滑坡稳定安全系数的降低,可给出计算位移和位移速度的演变过程。图5列出了不同稳定安全系数条件下滑坡位移速度-时间关系曲线,图5(a)为稳定安全系数1.10时的位移速度-时间曲线,随着时间的增长,位移速度-时间曲线趋于零,即为稳定状态;图5(b)、图5(c)显示变形速率趋于常数,表明坡体处于等速蠕变和弱变形阶段;图5(d)、图5(e)显示变形速率逐渐增大,表明坡体处于加速蠕变和强变形阶段。当稳定安全系数为1.01或1.00时,计算失真,此时坡体处于临滑阶段。根据数值计算指标进行的滑坡蠕变破坏演化过程的阶段划分与评价指标见表2。其中,等速蠕变阶段的滑坡稳定安全系数取1.10~1.04,是从偏于安全考虑的。
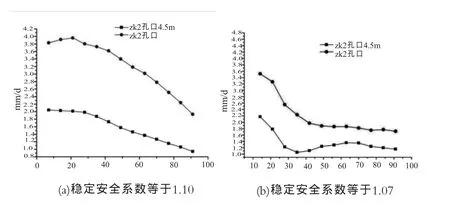
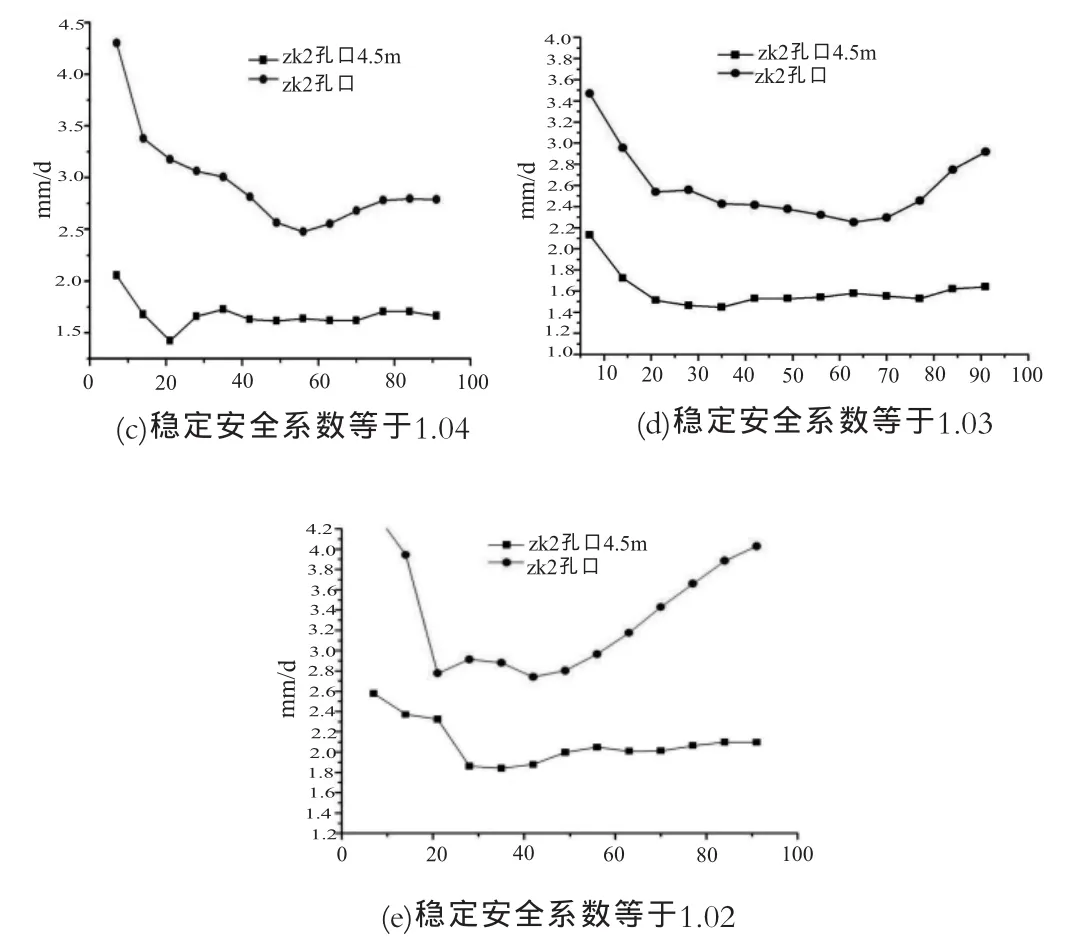
图5 不同稳定安全系数时的位移速度-时间曲线
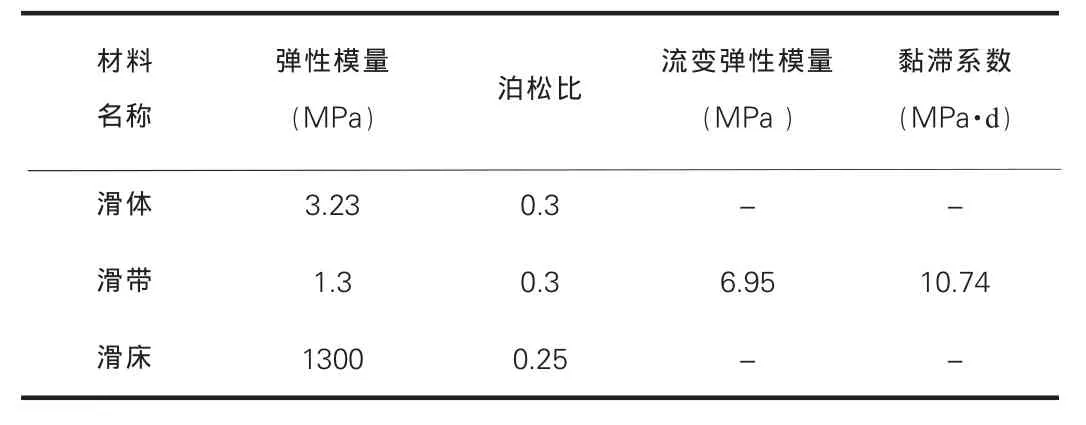
表2 滑坡体物理力学参数表
2.2 滑动面的发展过程
滑坡的蠕变破坏是一个渐进累积的过程,坡体内的滑动面,在外部环境作用下随着应力转移和调整而不断扩展,直至贯通的滑动面完全屈服,最后发展到滑动面整体破坏。传统的分析方法不仅无法显示滑动面的贯通过程,更不能直接显示滑面的受力、变形与破坏的全过程,而采用有限元强度折减法则可以较好地解决上述问题。通过分析不同折减系数条件下,即不同稳定安全系数下坡体内的塑性应变增量云图,可以直观地看到坡体内的滑动面随稳定安全系数的降低而逐渐扩展并贯通,直至破坏的全过程,滑坡失稳时的稳定安全系数为1.00。
三峡库区某堆积层滑坡如图6所示。
该滑坡稳定性主要受到降雨与库水位上升到156m后库水浸泡的影响,计算中应考虑滑体与滑带强度降低。由于库水位变动不大,对稳定性影响很小,因此不予考虑。计算中不能直接采用勘察设计时的强度参数,但对泊松比、弹性模量可采用试验数据,黏滞系数则采用基于监测位移的复变量求导法反演确定[11-13],可以得出滑带土的黏滞系数为,滑坡体物理力学参数见表2。

图6 滑坡地质模型
由于滑体与滑带受雨水和库水入渗影响,强度已经降低,不能采用勘察时的强度参数,这里先求出坡体失稳临界状态,即稳定安全系数为1.00时对应的c、tanφ值,然后按照比例增加c、tanφ值,给出稳定安全系数为1.08、1.05、1.04、1.03、1.02、1.01时的c、tanφ值, 再采用黏弹塑性或弹塑性模型计算剪切应变增量(图7),由此可以看出滑面的塑性区与剪切塑性应变的发展过程。由图7可以看出,当稳定安全系数为1.05时,滑面塑性区接近贯通;稳定安全系数为1.03时,塑性区完全贯通,但整个滑面尚未达到极限应变状态,计算还收敛,不会发生整体破坏,直到稳定安全系数为1.01时,滑面即将破坏。图7能直观、定量地显示滑面的受力、变形到破坏的演变全过程,这是当前蠕变破坏机理定性分析做不到的。
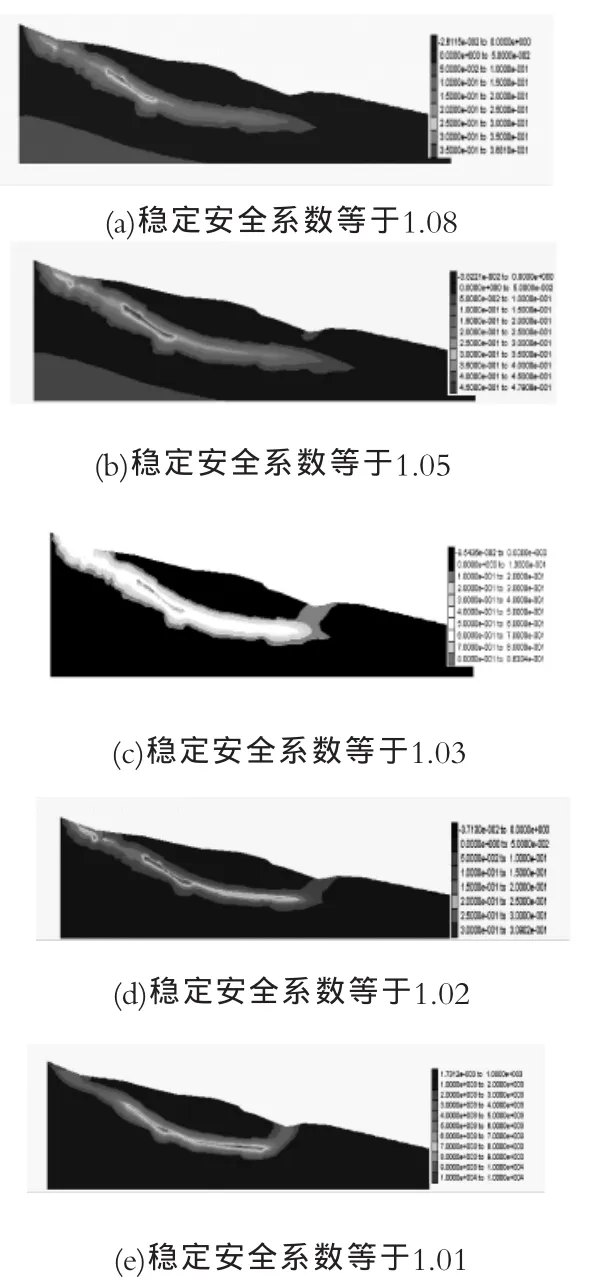
图7 剪切应变增量云图
2.3 滑坡实时稳定安全系数的确定与滑坡的预警预报
滑坡稳定性的定量分析,最重要的就是确定滑坡实时的稳定安全系数。通过不同稳定安全系数对应的计算位移-时间曲线与监测时间曲线的对比,可以较为准确地判断滑坡的实时稳定状态,即可确定滑坡实时稳定安全系数。
计算位移-时间曲线与监测位移-时间曲线的对比,主要看两者的曲线斜率是否一致,因为它与稳定安全系数有很好的一致性,此外也可以参看总位移量的大小是否一致。如图4所示,不管从监测曲线的斜率变化来看,还是从总位移量来看,都与稳定安全系数1.04的计算曲线相近,由此可判断该滑坡此时的稳定安全系数为1.04左右,这样就可以确定滑坡实时稳定安全系数,并能明确知道当前滑坡处于哪一稳定阶段,这对滑坡的预警预报起着关键作用。
滑坡实时稳定安全系数的确定对滑坡变形阶段的划分与预警预报有着重要作用,当稳定安全系数在1.10~1.04时,滑坡处于弱变形阶段;1.04~1.01时处于强变形阶段;小于1.01时处于临滑阶段。这都可以通过滑坡实时稳定安全系数加以预报。而临滑阶段还可以采用更为准确的预警方法,如采用回归与智能方法相结合的修正斋藤预报公式,以确定准确的滑坡日期。只要提供的监测数据是临滑或接近临滑的监测数据,采用上述方法一般都能达到理想的预测结果。由上可见,滑坡蠕变破坏演化机理可从观察、监测、计算三个方面分析,最终得到可视的、定量的、可预测的滑坡变形破坏机理与时空规律,并为滑坡的准确预报提供可靠依据。
[1]Zienkiewicz O.C,Humpheson C,Lewis R.W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.
[2]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.
[3]郑颖人,赵尚毅,李安洪,等.有限元极限分析法及其在边坡中的应用[M].北京:人民交通出版社,2011.
[4]郑颖人,赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报,2005,38(1):91-98.
[5]谭万鹏,郑颖人,陈卫兵.动态、多手段、全过程滑坡预警预报研究[J].四川建筑科学研究,2010,36(1):106-111.
[6]郑颖人,陈祖煜,王恭先,等.边坡与滑坡工程治理[M].北京:人民交通出版社,2007.
[7]Satio M.Forecasting the time of occurrence of a slope failure[A].In:Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering[C].Montre al,Que.Pergamon Press,Oxford,1965:537-541.
[8]李秀珍,许强,黄润秋,等.滑坡预报判据研究[J].中国地质灾害与防治学报,2003,4(14):5-11.
[9]陈卫兵,郑颖人,冯夏庭,等.考虑岩土流变特性的强度折减法研究[J].岩土力学,2008,29(1):101-105.
[10]谭万鹏,郑颖人,王凯.考虑蠕变特性的滑坡稳定状态分析研究[J].岩土工程学报,2010,32(Supp.2):5-8.
[11]LYNESS J.N,MOLER C·B.Numerical differentiation of analytic functions[J].SIAM Journal of Numerical Analysis,1967,4(2):202-210.
[12]谭万鹏,郑颖人.岩质边坡弹粘塑性计算参数位移反分析研究 [J].岩石力学与工程学报,2010,29(Supp.1):2988-2993.
[13]刘明维,郑颖人,张玉芳.一种基于复变量求导法的岩土体抗剪强度参数反演新方法 [J].计算力学学报,2009,8(6):676-683.

