球形障板对矢量传感器测向的影响*

莫世奇 ，方尔正，李海霞，杨德森

(1.海军装备研究院，北京100161;2.哈尔滨工程大学水声技术重点实验室，哈尔滨150001)

矢量传感器由声压传感器和振速传感器组合而成，对声场中一点处的声压和质点振速可以进行空间共点、同步测量。其中，声压传感器无指向性，振速传感器的各通道均具有“8”字形指向性，利用单个传感器获取到的声压和振速信息便可完成测向工作。实际工程应用中，需要把矢量传感器固定在如舰船球鼻艏或者球形导流罩等载体上进行作业。这些载体的散射作用必然会导致传感器的输出结果发生畸变，影响测向结果［1－7］。因此，进行球形障板对矢量传感器测向影响的研究，可为工程应用中传感器的安装及测向校正工作提供帮助。

目前对前述问题的研究工作主要采用理论推导进行，但除了最简单的刚性球壳可以通过理论推导得到解析解外，当采用其它不同声学模型和不同特性结构时，则难以进行计算［8－15］。而采用 ANSYS软件进行建模并配合SYSNOISE软件进行求解是解决这一问题的良好手段［16］。本文中采用这一方法针对球形障板声散射对矢量传感器测向输出的影响进行了仿真研究，并通过水池实验进行了验证。

1 球形障板散射模型

不失一般性地假设球形障板位于声场中，假设内部真空的弹性球壳位于无限均匀的水介质中，水的密度ρ1，水中声速为c1。令弹性球壳的球心与坐标系的原点重合，且入射平面波的传播方向与x轴正向一致，弹性球壳的内外半径分别为b和a，M点处为待考察声场点，如图1所示。

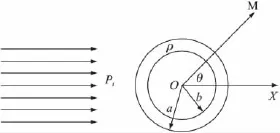
图1 球形障板声散射计算模型

根据《声学理论基础》书中的描述可知，入射平面波的声压可表示为对一系列球函数进行求和运算［17］:

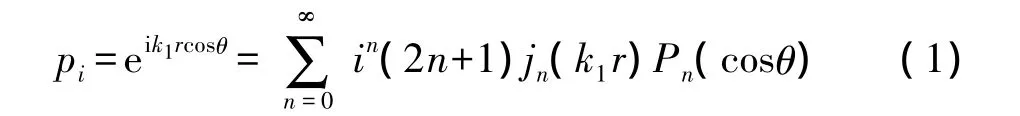
其中，k1=ω/c1为弹性球壳外部介质中的波数，且忽略了时间因子e－iωt。根据式(1)可推出，弹性球壳外部散射声压ps为:

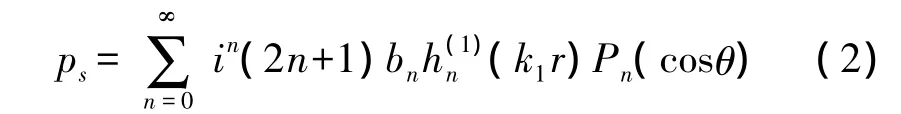
总声场为:

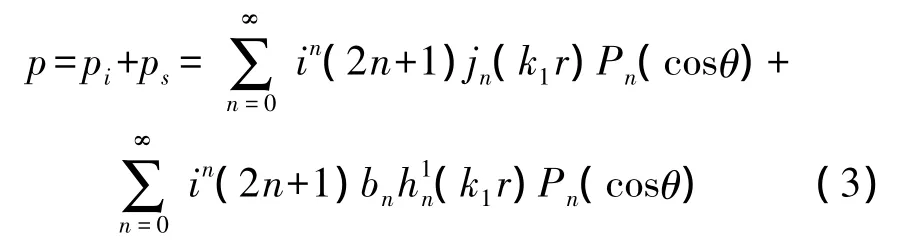
其中，bn为常数，其值由边界条件决定。

声波由x轴正方向入射，则声场关于x轴向对称分布，其产生的散射声场也是对称分布，可知式(2)中 n=0。

通过对式(2)求解可以得到散射声场，与入射声场进行叠加后可以得到总声场模型。对于矢量传感器来讲，在式(2)基础上除了需要对散射声压进行计算外，还需进行质点振速散射场的计算。球形障板的散射声压场可以通过上两式求出，其振速场的计算通常要通过尤拉方程对散射声场的径向和轴向质点振速获得。

2 有限元和边界元方法声场计算

采用有限元和边界元联合建模的方法可对上述过程实现精确的求解。与常用的Kirchhoff近似方法和T矩阵法不同，在此处采用主要通过间接边界元流体模型和有限元结构模型耦合的方法实现整个计算过程。

将图1中的声学模型在物理坐标系中进行建模，可以得到如下耦合系统方程:

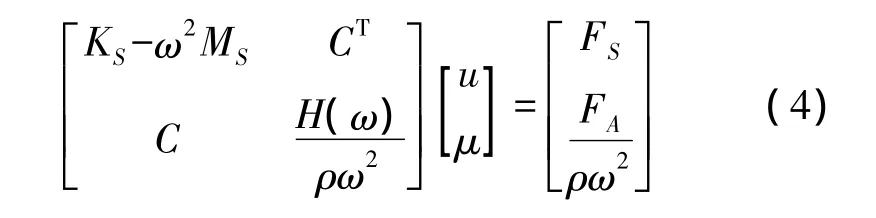
式中KS表示结构模型的刚度矩阵;MS表示结构模型的质量矩阵;C表示几何耦合矩阵;H(ω)表示间接边界元影响;FS表示结构模型的载荷向量;FA表示流体模型的载荷向量;u表示节点位移;μ表示节点压力跳动量。

图2 ANSYS和SYSNOISE软件工作流程

对球形障板混合声场对矢量传感器定位影响的计算流程见图2。全流程分为两个部分进行，第一部分为采用ANSYS系统进行建模工作，建立好的障板模型经过网格划分生成节点和单元数据文件后传递给SYSNOISE软件进行分析计算。通过设定分析类型和设置各个求解参数，进行计算得出分析结果。

下面通过算例给出图2中分析方法的计算过程。根据图1中的参数，设定球形障板半径为0.11 m，单元尺寸为0.025 m，单元类型为 Shell 63。在SYSNOISE中，设定耦合模型为 BEM Direct Collecation Node Exterior Coupled Frequency，球形障板为0.004 m厚的45号钢，密度为7 850 kg/m3，泊松比为0.28，杨氏模量为 2.1×1011N/m2。设定流体为水，声速为1 500 m/s。计算结果如图3所示。

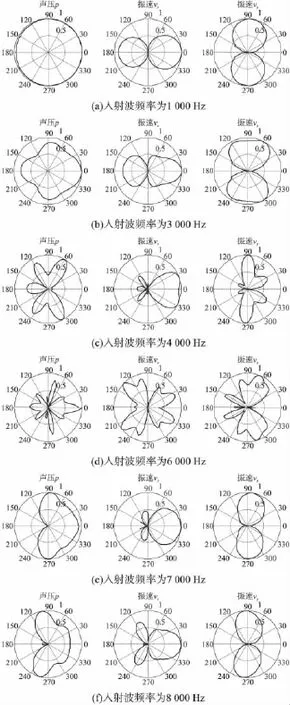
图3 不同方向入射波入射时声学参量的角分布函数曲线图

通过图3的结果可以看出，球形障板散射作用的影响，导致矢量传感器所在场点的声压、振速分量的角分布函数曲线在1 000 Hz～3 000 Hz时变化比较缓和;在4 000 Hz～6 000 Hz时变化较为复杂;在7 000 Hz～8 000 Hz时变化又比较缓和。这说明，球障板的声散射在信号频率4 000 Hz～6 000 Hz区间对传感器的测量结果影响大，在1 000 Hz～3 000 Hz和7 000 Hz～8 000 Hz区间对传感器的测量结果影响小。

3 矢量传感器测向误差分析

矢量传感器应用于方位估计，通常是探测远距离目标，满足远场条件，声波可近似为平面波传播。在理想的流体介质情况下，平面波声场中的声压函数为:

利用尤拉方程可求出振速函数:

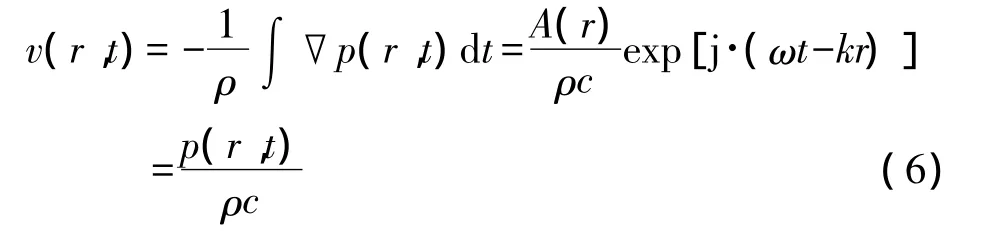
可以看出，声压与振速之间只相差一个系数——波阻抗ρc。假设利用矢量传感器所测得的空间一点处声压和质点振速信号，已经消除掉波阻抗ρc的影响，归到相同的量纲中，忽略传感器声压与振速灵敏度的差异，可以认为所测得的声压量p(r，t)与振速量v(r，t)相等，则矢量传感器所测得的声压信号与空间3个方向的质点振速信号可以表示为:

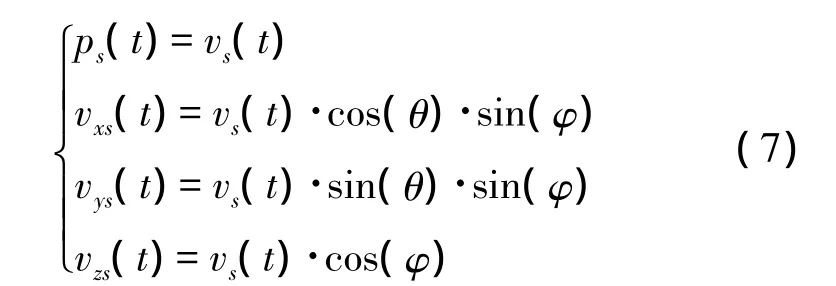
θ为入射声波的水平方位角，φ为入射声波的仰角。

可以利用声压与三个方向质点振速的各种组合运算来求得水下目标的方位信息。目前，较为常用的算法是声强法测向。

声压与质点振速的乘积为声强(声能流)。考虑水平方位情况，利用矢量传感器对水平方位为θ的声源进行测量，可以分别得到x、y方向的声强信息：

利用平均声强法估计各个频率的水平方位:

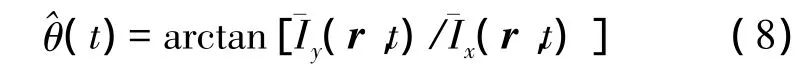
除了平均声强法，矢量传感器还可以采用平均振速、互谱声强等方法进行被动方位估计。但是，上述各种方法都是基于自由空间进行的，在有障板存在的条件下，由于散射声波的影响，将会对大大降低矢量传感器的测向精度。下面用一组仿真数据进行具体分析。

令传感器到障板的距离为d，声波入射角度为θ。利用FEM+BEM法计算出的声场参量值，采用质点振速法［6］对 θ=10°，d=0.21 m、d=0.41 m 和 d=1.11 m条件下的测向误差进行分析:

图4、图6与图8的横轴为声波频率，纵轴为声压及振速的幅值;图5、图7与图9的横轴为声波频率，纵轴为测向误差的绝对值。

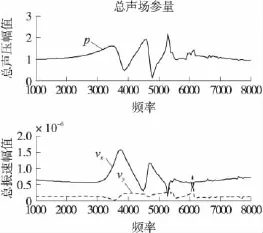
图 4 d=0.21 m，θ=10°时总声场参量曲线

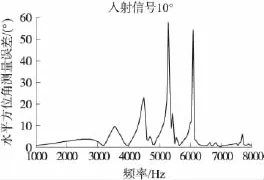
图5 d=0.21 m，θ=10°时测向误差

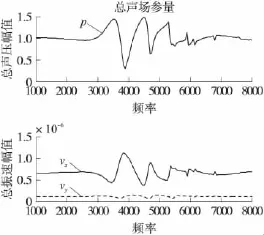
图 6 d=0.41 m，θ=10°时总声场参量曲线

由图4～图9可以看出:

(1)在θ=10°的相同入射波条件下，随着传感器与障板距离的增大，传感器接收到的声压和各轴向振速的最大幅值均随之减小，且测向误差总体减小。

(2)在1 000 Hz～3 000 Hz、7 000 Hz～8 000 Hz时，传感器的测向误差起伏较小，在 3 000 Hz～7 000 Hz区间，传感器的测向误差起伏很大，即:该频段在球形障板的散射作用容易产生谐峰，从而严重影响测量结果。该结论该场点声学参量的角分布函数曲线的结论对应。

图7 d=0.41 m，θ=10°时测向误差

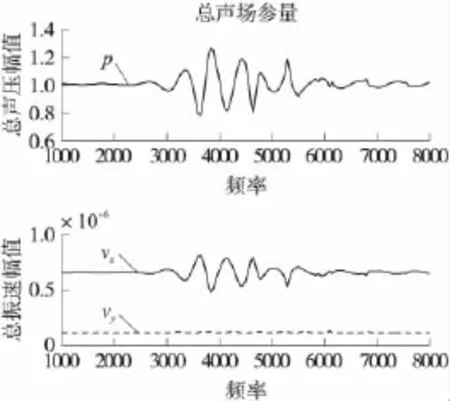
图8 d=1.11 m，θ=10°时总声场参量曲线

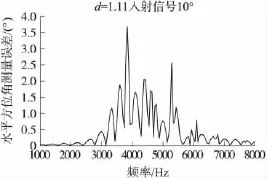
图9 d=1.11 m，θ=10°时测向误差

4 水池试验数据分析

试验在哈尔滨工程大学消声水池进行，使用的弹性球的半径为0.11 m，将传感器中心到球中心的距离设置为0.21 m，声源与矢量传感器之间的距离设置为1.7 m，按1/3倍频程从2 000 Hz～8 000 Hz发射单频连续信号，在0～360°之间，每间隔5°转动一次。

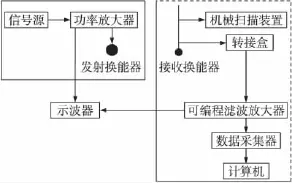
图10 试验设备连接示意图

通过试验测量得到的矢量传感器所在场点的声学参量的角分布函数曲线图具体如下:

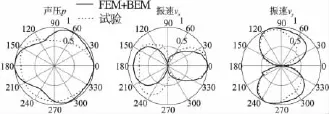
图11 2500Hz时矢量传感器试验测量结果与FEM+BEM结果对比

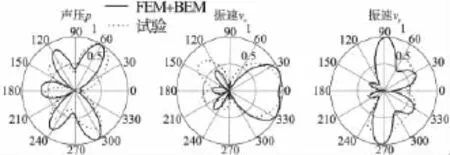
图12 4000Hz时矢量传感器试验测量结果与FEM+BEM结果对比

图13 8000Hz时矢量传感器试验测量结果与FEM+BEM结果对比

图11至图13为矢量传感器指向性的理论与试验结果对比，可以得出:

(1)在信号频率为2 500 Hz和8 000 Hz时，球散射导致矢量传感器所在场点的声压、振速分量的角分布函数曲线的复杂程度小于4 000 Hz时曲线的复杂程度。这就验证了前述的理论，即:球形障板近场声学参量的角分布函数曲线在信号频率1 000 Hz～3 000 Hz时较简单;在3 000 Hz～7 000 Hz时较复杂;在7 000 Hz～8 000 Hz时又趋于简单。

(2)通过试验验证，球形障板近场声学参量的角分布函数曲线关于θ=0°极坐标轴对称。

针对入射角度 θ=10°时 d=0.21 m、d=0.41 m以及 θ=30°时 d=0.21 m、d=0.41 m 时采集到的数据进行分析。

图14 球形障板试验测向结果

图14横轴为声波频率，纵轴为测向误差的绝对值，通过分析可以初步得到以下结果:

(1)在相同角度入射波的前提下，随着矢量传感器声中心至球障板中心间距d的增大，得到的测向误差总体上减小。

(2)验证了在3 000 Hz～7 000 Hz时，弹性球障板的声散射导致矢量传感器的测向误差起伏较大;在1 000 Hz～3 000 Hz和7 000 Hz～8 000 Hz时传感器测向误差比较稳定这一结论的正确性。

(3)消声水池试验得到的测向误差与FEM+BEM法得到的测向误差吻合的比较好，偏差均在5°之内。造成试验结果与FEM+BEM法偏差的原因主要有:(a)发射换能器、传感器、球障板的声中心没有完全在xoy平面内，即:存在一定的俯仰角;(b)消声水池对3 150 Hz以上的信号频率消声效果较好，因此2 000 Hz与2 500 Hz时的理论与实验存在偏差;(c)由于试验中采用的是2 000 Hz～8 000 Hz区间的7个1/3倍频程中心频率的频点，且该频率段大多处于弹性球障板的强共振频率范围内，因此在该共振频率区间内，传感器对测量频率、测量环境等因素十分敏感，极易造成试验结果与理论结果的偏差。

5 结论

本文运用有限元和边界元相结合的方法对球形障板的水下散射声场进行了计算，并采用质点振速法对相应条件下的测向误差进行了分析，通过理论分析和水池试验验证了传感器的测向误差随距离的增大而减小，且在3 000 Hz～7 000 Hz时测向误差起伏较大、在1 000 Hz～3 000 Hz和7 000 Hz～8 000 Hz时测向误差起伏较小的结论。因此，在工程应用中需根据实际障板条件，选择合适的工作频段和安装位置，将障板对矢量传感器测向的影响降到最低。

［1］ Barton J P，Nicholas L W，Haifeng Zhang，et al.Near-Field Calculations for a Rigid Spheroid with an Arbitrary Incident Acoustic Field［J］.Journal.Acoust.Soc.Am，2003，113(3):1216－1222.

［2］ Rapids B R，Lauchle G C.Vector Intensity Field Scattered by a Rigid Prolate Spheroid［J］.Journal.Acoust.Soc.Am，2006，120(1):38－48.

［3］ Javad Ahmadi-Shokouh，Hengameh Keshavarz.A Vector-Hydrophone’s Minimal Composition for Finite Estimation-Variance in Direction-Finding Near/Without a Reflecting Boundary［J］.IEEE Transactions on Signal Processing，2007，55(6):2785－2794.

［4］ 惠俊英，惠娟.矢量声信号处理基础［M］.国防工业出版社，2009:6－29.

［5］ 刘细宝，张国军，薛晨阳，等.矢量水听器的芯片级减震结构的设计［J］.传感技术学报，2011(6):835－838.

［6］ 许姣，张国军，石归雄，等.纤毛式矢量水听器新型封装结构的研究［J］.传感技术学报，2011(4):517－521.

［7］ 时胜国.矢量水听器及其在平台上的应用研究［D］.哈尔滨:哈尔滨工程大学，2006.

［8］ 生雪莉，郭龙祥，梁国龙.球型软障板矢量水听器指向性研究［J］.声学技术，2002，21:59－60.

［9］ 侯玉敏，毛卫宁.刚性曲面障板散射对多模球形水听器测向的影响［J］.声学技术，2005，24(2):94－97.

［10］王之海，孙贵新，张巍．球形障板对矢量水听器接收性能的影响［J］．中国新技术新产品，2010(9):1－2．

［11］张揽月，杨德森，张巍．刚硬球型障板散射对矢量线阵的性能影响［J］．声学技术，2009，8(2):103－104．

［12］ 杨士莪．弹性体目标散射特性［J］．物理学进展，1996，16(3):497－503．

［13］冀邦杰，杨宝民，王海陆．有限平面障板对低频指向性的影响［J］．声学技术，2007，26(4):588－591．

［14］方开翔，唐春丽．导流罩和声障板对声纳尾部声场影响的数值模拟［J］．噪声与振动控制，2004，1:16－19．

［15］宋晓雪．曲面障板近场声散射对矢量水听器测向影响［D］．哈尔滨工程大学，2008．

［16］李增刚．SYSNOISE Rev 5．6详解［M］．北京:国防工业出版社，2005．

［17］何祚镛，赵玉芳．声学理论基础［M］．北京:国防工业出版社，1981:315－327．