滑动离散傅里叶算法输出稳定性研究
王宏伟
(西安邮电大学,陕西 西安 710121)
引 言
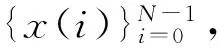
(1)
式中索引只有频域索引k。连续计算窗口(窗口长度等于数据帧长度N)滑动后的频谱,便引入时域索引n,可以进行基于矩形窗的短时傅里叶变换(STFT)的时频分析,即
n≥N-1
(2)
窗口滑动分为不重叠滑动和重叠滑动。对输入数据分段(每一段数据称为一帧数据)的常用方法是不重叠滑动,即从0到N-1,然后从N到2N-1,如此一直下去。另一种方法是对数据帧进行一定程度的重叠处理。例如滑动步长为d时,第一帧取0到N-1点,第二帧取d到d+N-1,第三帧取2d到2d+N-1,依次类推。数据帧最大重叠滑动时为逐点滑动,即第一帧取0到N-1,第二帧取1到N,第三帧取2到N+1,依次类推。
数据逐点滑动时,相邻窗口内的数据样本有着很大的相似性,后一个时刻窗口样本只是将前一个时刻窗口样本的第一个样本舍弃,在最后添加一个新的样本,因此,两个连续时刻窗口样本对应的频谱必然存在联系,逐点滑动DFT算法[1-4]正是基于这样的思想进行计算量的优化。
由于数字系统的有限字长效应,存在量化误差和舍入误差。滑动DFT算法是一种反复迭代的运算,量化误差和舍入误差会随着迭代次数的增加而不衰减的传播,且随着时间逐步积累,导致系统失稳。有限字长效应对定点处理数字系统影响的比对浮点处理的数字系统影响更大。
目前解决滑动DFT算法输出不稳的方法主要有加入衰减因子法[1-2],自适应最小均方误差(LMS)算法[3-4]。本文利用改进Goertzel算法的递归单元改造滑动DFT算法的频率单元,使其具有定期自动清零功能,解决了滑动DFT频率单元输出不稳定问题。
1 改进Goertzel算法的递归单元
图1(a)为计算DFT谱X(k)的改进Goertzel算法的单极点递归单元[5],其对应的差分方程为
r=1,2,…,N
(3)
式中:r为迭代次数;yk(r)表示第r次迭代结果。令初始状态yk(0)=0,则
可见,经过N次循环迭代后,得到了我们期望的输出X(k)=yk(N)。当输入为复数序列时,每次迭代需要1次复数加法和1次复数乘法,N次迭代共需要N次复数加法和N次复数乘法。
式(3)对应的传递函数为
(4)
这是只有一个极点z=ej2πk/N的一阶无限脉冲响应(IIR)系统(IIR指具有反馈通道的系统),但只需进行有限次循环迭代运算。式(4)做如下变换
(ej2πk/N-z-1)
(5)
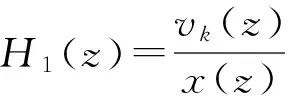
则Hk(z)=H1(z)H2(z).
H1(z)有两个极点z=e±j2πk/N,对应的差分方程为
vk(r)= 2cos(2πk/N)·vk(r-1)-
vk(r-2)+x(r-1)
(6)
式中r=1,2,…,N,初始条件为vk(0)=vk(-1)=0.当输入为实数序列时,式(6)中1次迭代需要1次实数乘法和2次实数加法;N次迭代需要N次实数乘法和2N次实数加法。H2(z)对应差分方程为
yk(r)=vk(r)·ej2πk/N-vk(r-1)
(7)
只需要用式(7)计算当r=N时对应的输出yk(N)即可
yk(N) =vk(N)·ej2πk/N-v(k)(N-1)
=[vk(N)cos(2πk/N)-vk(N-1)]+
j·vk(N)sin(2πk/N)
=Re[X(k)]+j·Im[X(k)]
=X(k)
(8)
式(8)是在式(6)N次循环迭代完成后再进行实部和虚部的计算,式(8)只需要2次实数乘法和1次实数加法。图1(b)是实现式(6)和式(8)所示差分方程的双极点递归单元,该递归单元计算量为N+2次实数乘法和2N+1次实数加法。由于全部为实数运算,硬件实现结构简单,计算量少。
图1所示的两种改进Goertzel算法的递归单元都具有选择性计算DFT谱X(k)的优点。递归单元的输入序列依次为x(0),x(1),…,x(N-1),适合于输入一个数据,便处理一个数据,但要等N次循环迭代后再输出结果。当输入为复数数据时,一般用图1(a)单极点递归单元计算DFT谱;而当输入为实数数据时,选用图1(b)双极点递归单元计算DFT谱。
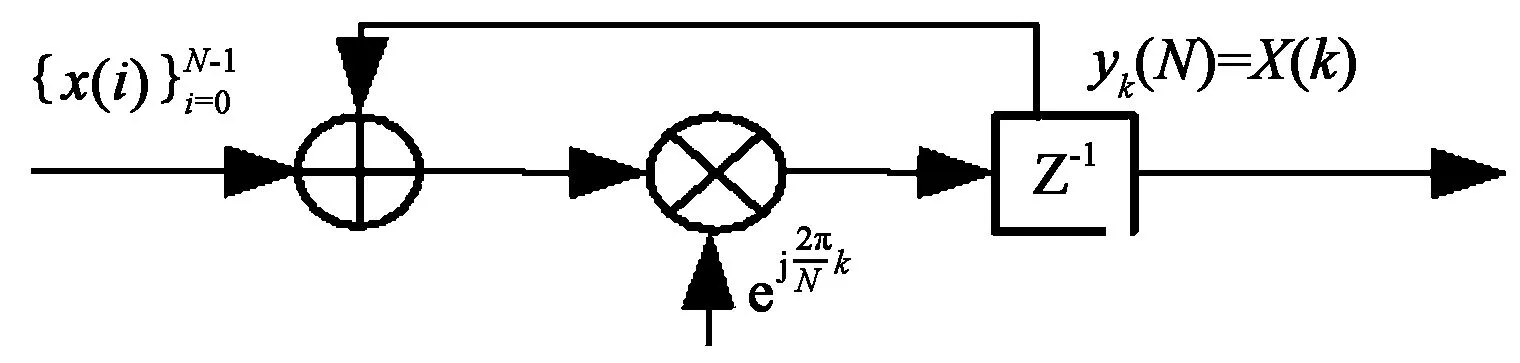
(a) 单极点递归单元
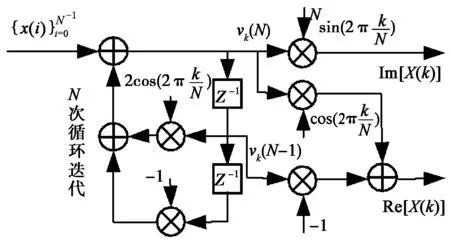
(b) 双极点递归单元 图1 改进Goertzel算法的递归单元
2 逐点滑动DFT算法介绍
2.1 逐点滑动DFT算法的频率单元
设在n-1时刻,滑动窗口选中的N个样本数据为{x(n-N),x(n-N+1),…,x(n-2),x(n-1)};在n时刻,滑动窗口选中的N个样本数据为{x(n-N+1),x(n-N+2),…,x(n-1),x(n)}。根据DFT理论,在n-1时刻,第k个频率单元的频谱为
X(n-1,k)=x(n-N)+x(n-N+1)e-j2πk/N+
…+x(n-2)e-j2πk·(N-2)/N+
x(n-1)ej2πk·(N-1)/N
(9)
在n时刻,第k个频率单元的频谱为
X(n,k)=x(n-N+1)+x(n-N+2)e-j2πk/N+…+
x(n-1)e-j2πk·(N-2)/N+x(n)ej2πk·(N-1)/N
(10)
比较式(9)和(10)可以得到差分方程,即逐点滑动DFT算法的差分方程[1-4]
X(n,k)= [X(n-1,k)-x(n-N)]ej2πk/N+
x(n)e-j2πk(N-1)/N
(11)
式(11)可以化简为
X(n,k)=ej2πk/N{X(n-1,k)-x(n-N)+x(n)}
(12)
由式(12)可知,要计算n时刻谱值X(n,k),只要将前一个时刻n-1的谱值X(n-1,k)减去一个旧样本x(n-N),加上一个新样本x(n),再乘以权系数ej2πk/N即可。图2(a)是实现式(12)差分方程的单极点频率单元图。
式(12)对应的传递函数H(z)为
(13)
这是只有一个极点z=ej2πk/N的一阶IIR系统(具有反馈通道),随着时域索引n→∞,需要进行无限次循环迭代运算。对式(13)再作如下变换:
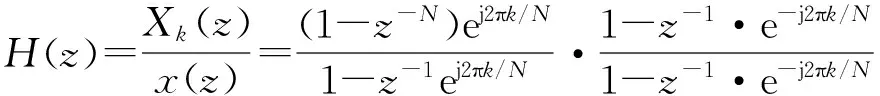
(14)
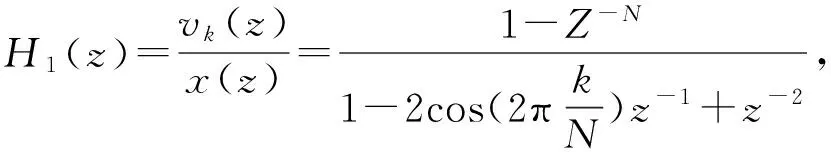
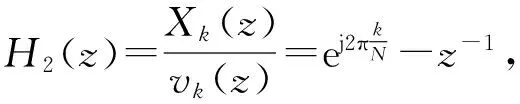
vk(n)= 2cos(2πk/N)·vk(n-1)-vk(n-2)+
x(n)-x(n-N)
(15)
H2(z) 对应的差分方程为
X(n,k)=vk(n)·ej2πk/N-vk(n-1)
=[vk(n)cos(2πk/N)-
vK(n-1)]+
j·[vk(n)sin(2πk/N)]
=Re[X(n,k)]+j·Im[X(n,k)]
(16)
图2(b)是实现式(15)、(16)差分方程的双极点频率单元图。
当输入序列为复数数据时,一般用图2(a)单极点频率单元实现逐点滑动DFT.在一个频点k处,仅仅需要2次复数加法和1次复数乘法就可以完成频谱X(n,k)的计算。由于计算机实现时,复数运算需要转化为实数运算实现,即1次复数与复数的乘法需要4次实数乘法和2次实数加法,1次复数与复数加法需要2次实数加法。因此,图2(a)单极点频率单元共需要有4次实数乘法和6次实数加法来完成频谱X(n,k)的计算。
当输入为实数数据时,选用图2(b)双极点频率单元实现逐点滑动DFT.在一个频点k处,仅仅需要3次实数乘法和4次实数加法就可以完成频谱X(n,k)的计算。由于图2(b)中全部为实数运算,硬件实现结构简单,计算量少。
由图2可知,逐点滑动DFT算法的频率单元由一个梳状滤波器(左半部分)和一个复谐振器(右半部分)组合而成[1-2]。如果要同时计算M点频谱的短时傅里叶变换,只需要M个复谐振器并联即可。
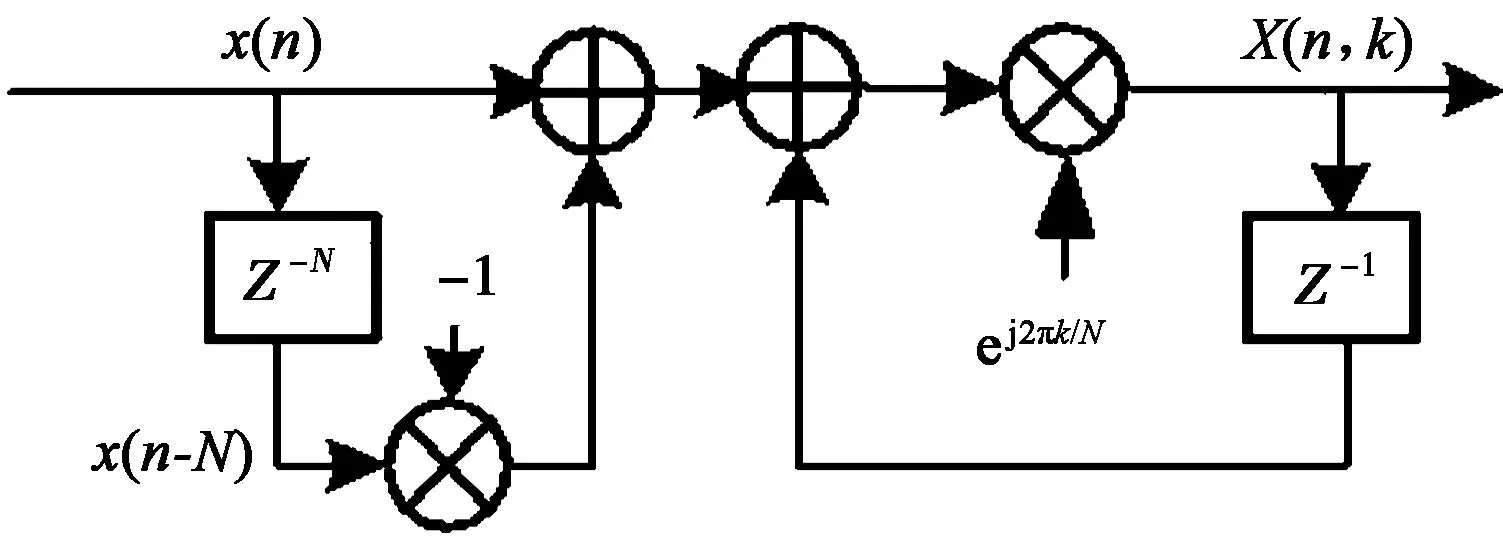
(a) 单极点频率单元
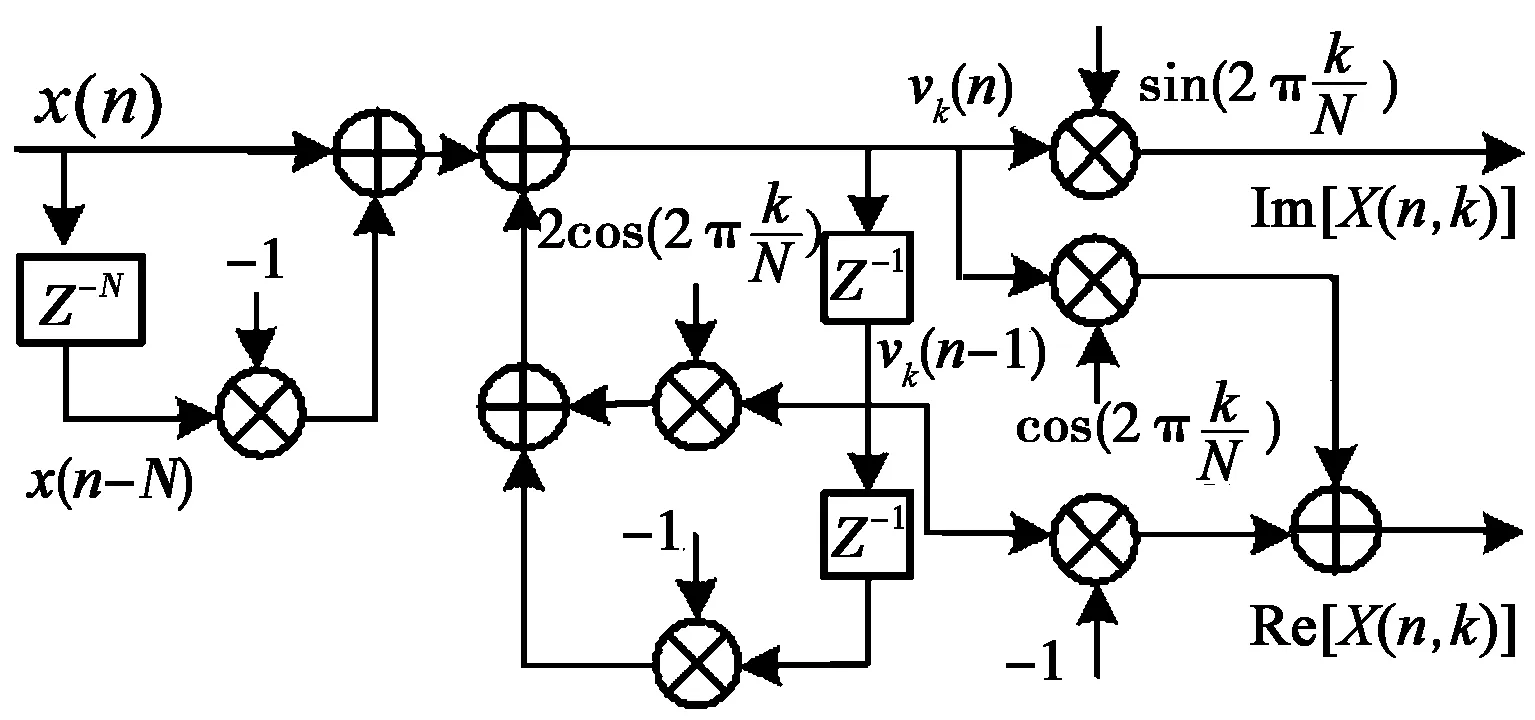
(b) 双极点频率单元图2 逐点滑动DFT算法的频率单元
2.2 逐点滑动DFT算法的优点
1) 逐点滑动DFT算法实现了频谱输出的可选择性。逐点滑动DFT算法采用的是单个频率单元的独立谱线计算,根据实际需要,可选择性计算感兴趣的谱线,这极大地提高了谱分析的灵活性。
2) 逐点滑动DFT算法优化了连续对信号进行STFT分析时的计算量。只要知道了前一时刻的频谱X(n-1,k),计算下一时刻频谱X(n,k)时,对于单极点频率单元,输入为复数数据时,仅需4次实数乘法、6次实数加法;对于双极点频率单元,输入为实数数据时,仅需3次实数乘法、4次实数加法,并且频率单元计算量与参数N的大小(即数据帧的长度N)无关。
3) 逐点滑动DFT算法频率单元的数据输入率与数据输出率相同,可以实时处理数据。FFT算法虽然能以较快的速度计算出全部N点离散频谱,但其N点快速傅里叶变换(FFT)的数据处理时间至少包括N个时域样本的采集时间和时域数据向频域数据转换的计算时间。计算1帧N点FFT时计算量为2Nlog2N次实数乘法和2Nlog2N次实数加法,当数据帧窗口每滑动一个数据后,就需要再独立的完成1次N点FFT运算,即又需要2Nlog2N次实数乘法和2Nlog2N次实数加法。因此,用FFT算法计算窗口逐点滑动时的STFT运算是不现实的。而对于逐点滑动DFT算法,采集一个时域数据,输入到频率单元后,经过几次算术运算,便可以输出一个频域数据。如果在一个采样间隔时间内,能完成这固定且有限的几次算术运算,便可以做到边采样、边计算、边输出,从而实现了实时处理。
3 递归单元和频率单元的稳定性探讨
受数字系统有限字长的影响,表示信号和参加运算的各个参数精度将不再是无限的,存在量化误差;离散系统中的乘法运算将产生舍入误差,例如,两个8 bit的数相乘,其积是16 bit,但最后只能用8 bit来表示,因此,需要舍弃积的后8 bit,这必然产生数字运算的舍入误差(或截尾误差)。量化误差和舍入误差通过离散系统后,必然产生误差的积累效应,并在系统中无衰减传播,结果在系统输出端将会产生较大的误差。
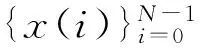
(17)
为了导出在递归单元输出端的信噪比,需要对信号作进一步的假设。由N点DFT的定义式(1),有
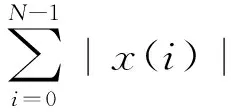
(18)
为了防止在运算过程中可能出现的溢出,需要对x(i)的幅度有所限制。不失一般性,假定对所有的i都有|x(i)|≤1,那么|X(k)|≤N;若需要|X(k)|≤1,那么只要将所有的x(i)都除以N即可。为了讨论方便,假定x(i)是在(-1/N,1/N)之间服从白噪声序列,则x(i)的方差为
=1/(3N2)
(19)
于是X(k)的方差为
=1/(3N)
(20)
在递归单元输出端,信号与舍入误差之间的信噪比为
=6.02b-20lgN
(21)
此处的信噪比(单位dB)指输出端信号量化表示精度[6]。对于N点DFT的单极点递归单元(图1(a)),若给定DFT的点数N=1 000,并要求SNR=10 dB,由式(21)可以求出所需字长b≈12bit.再如,已知运算单元的字长为20 bit,要求SNR=15 dB,那么由式(21)求出所能允许误差下的最大迭代次数N≈186 208.
对于N点DFT的双极点递归单元(图1(b)),求出系数X(k)需要N+2次实数乘法,因此,式(21)需要改写为
=6.02(b+1)-10lg(N2+2N)
(22)
对于逐点滑动DFT的频率单元(图2(a)或图2(b)),需要进行无限次循环迭代。当n→∞时,相当于式(21)或(22)中的N趋于无穷大,在有限字长运算单元组成的数字系统中,随着循环迭代次数的无限增加,信噪比越来越小,意味着输出端信号值的精度越来越差,导致输出结果不可靠。由于量化误差和舍入误差的积累与传播,逐点滑动DFT频率单元输出不稳定现象迟早会出现。
4 改进滑动DFT算法的频率单元
由上节讨论可知,改进Goertzel算法的递归单元和逐点滑动DFT算法的频率单元虽然都采用了具有反馈通路的IIR滤波器结构,但递归单元进行有限次循环迭代,在大字长运算单元组成的递归单元中,确实可以保证输出稳定;而频率单元则需要进行无限次循环迭代运算,因长时间的误差积累会出现输出不稳的致命缺点。
利用改进Goertzel算法的单极点递归单元(图1(a))来改造逐点滑动DFT算法的单极点频率单元(图2(a)),改进滑动DFT算法的单极点频率单元,如图3(a)所示。图3(a)上半部分为改进Goertzel算法的单极点递归单元,每输入N个点才会有一次输出Xr(lN-1,k);下半部分为逐点滑动DFT算法的单极点频率单元,每输入一个点便有一次输出Xs(n,k)。图3(a)中选择器模块的输出满足
X(n,k)=
(23)
利用改进Goertzel算法的双极点递归单元(图1(b))来改造逐点滑动DFT算法的双极点频率单元(图2(b)),改进滑动DFT算法的双极点频率单元,如图3(b)所示。图3(b)上半部分为改进Goertzel算法的双极点递归单元的反馈部分,每输入N个点才会有输出vr(lN-1,k),vr(lN-2,k) ;下半部分为逐点滑动DFT算法的双极点频率单元,每输入一个点便有输出vs(n,k),vs(n-1,k)。图3(b)中选择器1模块的输出满足
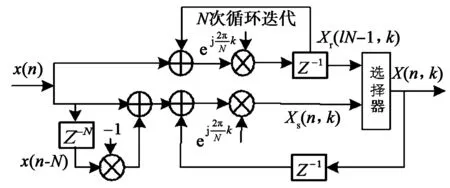
(a) 改进滑动DFT的单极点频率单元
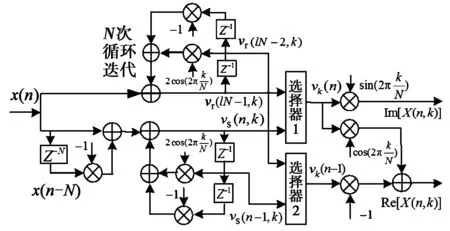
(b) 改进滑动DFT双极点频率单元 图3 改进滑动DFT频率单元
vk(n)=
(24)
选择器2模块的输出满足
(25)
由于单极点递归单元(图1(a))在N次循环迭代运算前需要令yk(0)=0;双极点递归单元(图1(b))在循环迭代运算前也需要令vk(0)=vk(-1)=0.计算机具体实现yk(0)=0或vk(0)=v(-1)=0时,需要对乘法器、加法器和锁存器等运算单元执行清零操作。改进Goertzel递归单元的自动清零操作防止了量化误差和舍入误差的进一步积累和传播。
由于递归单元有定期自动清零功能,则滑动DFT的频率单元的输出每隔N个值,便被递归单元的输出值替代一次,相当于定期给滑动DFT频率单元清零,并能提供准确的新谱值,所以改进滑动DFT的频率单元(图3)防止了误差的积累和传播。只要保证N次循环迭代运算中,递归单元的输出稳定(采用大字长的定点或浮点运算单元,扩大数值表示范围,可以保证输出稳定),则可保证改进滑动DFT频率单元的输出稳定。
5 计算机仿真
为了方便对比分析,以文献[4]列举的信号为例研究。信号x(n)=sin(2πF1·n/fs)+sin(2πF2·n/fs),其中F1=0.03 Hz;F2=1.1 Hz;采样频率fs=32 Hz.
5.1 首帧数据对应的频谱图计算
比较FFT算法和改进Goertzel算法得到的首帧数据对应的频谱图(图4),无论是幅频图,还是相频图都完全相同,从而验证了这两种算法都可以被用来计算信号的DFT谱。但FFT算法不管需要与否,会不加选择的计算出全部离散频谱,适合全景频谱分析;而改进Goertzel算法采取单根谱线的独立计算,具有选择性计算频谱的优点,适合感兴趣频点的频谱计算。
不论输入数据是实信号,还是复信号,N点FFT算法的计算量均指复数乘法和复数加法,那么32点FFT需要(N/2)log2N=16log232=80次复数乘法和Nlog2N=32log232=160次复数加法。
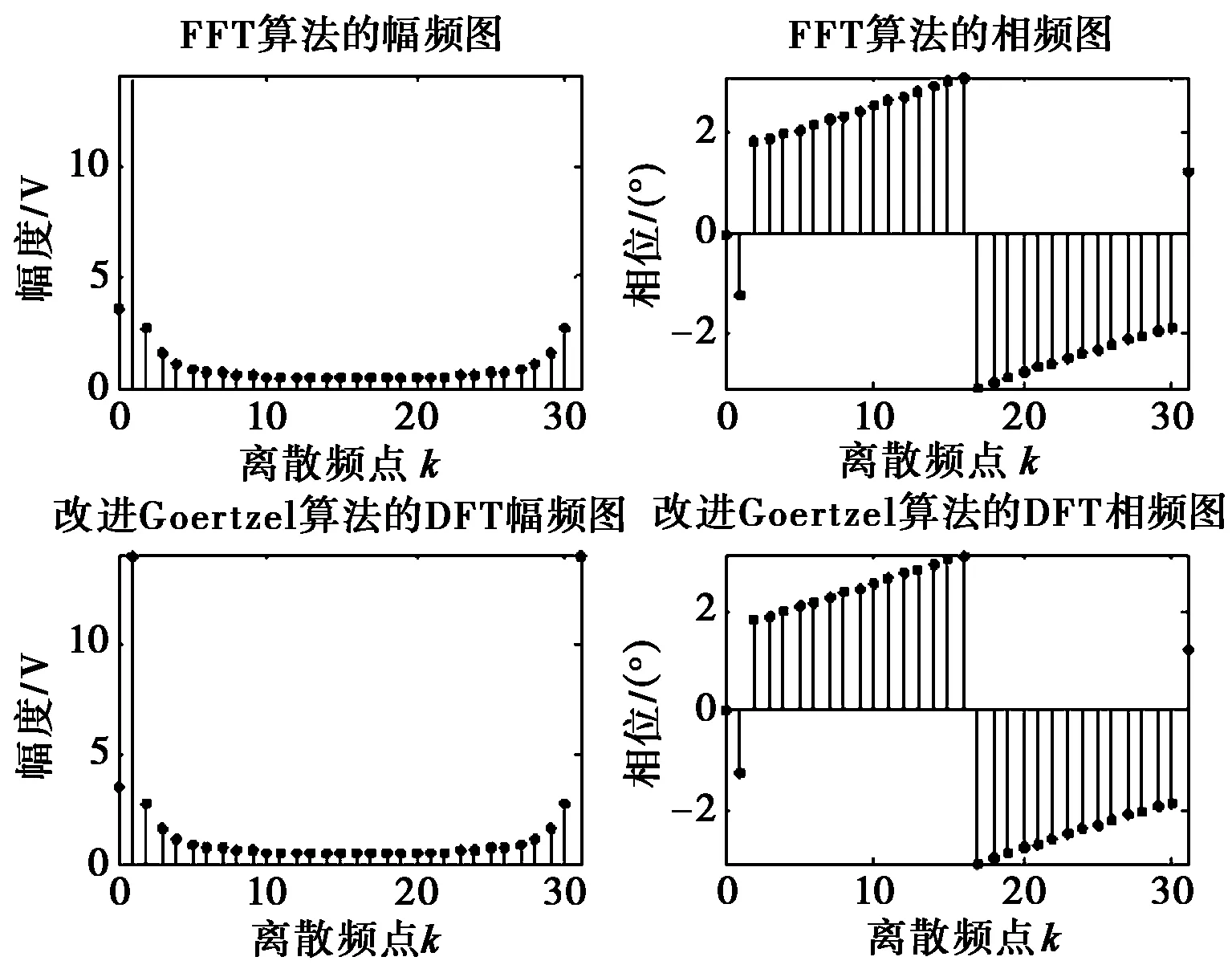
图4 两种算法得到的频谱图比较
输入实信号时,如果以1路改进Goertzel算法的双极点递归单元(图1(b))为运算模块,依次计算全部N=32点频谱时,计算量为N(N+2)=1 026次实数乘法和N(2N+1)=2 080次实数加法。当然,若考虑了某些频点的特殊性和DFT谱的对称性还可以进一步减少计算量。例如根据式(1),有
X(0) =X(k)∣k=0
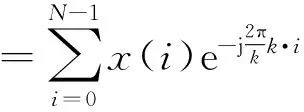
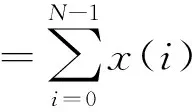
(26)
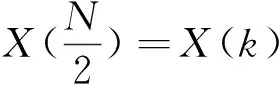
(27)
=x(0)-x(1)+x(2)-x(3)+…+
(-1)N-1x(N-1)
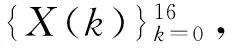
本文将改进Goertzel算法的递归单元与滑动DFT算法的频率单元集成在一起构成改进滑动DFT算法的频率单元,只负责一个指定频点的DFT谱计算;如果需要计算多个指定频点或局部频段的多个频点DFT谱,一般需要多路频率单元构成并行运算模块。此时模块的计算量(或计算速度)只需考虑单路递归单元的计算量(或计算速度)即可。对于本例,单路递归单元计算量为N+2=34次实数乘法和2N+1=65次实数加法。与FFT算法不同,改进Goertzel算法不必等参与运算的数据都准备好,可以边采集数据、边计算频谱,具有很好的实时性。
5.2 有限字长效应对滑动DFT输出影响
作N=32点的逐点滑动DFT。将每个时刻m对应DFT谱各个分量的模平方(功率)累加起来,除以N作为输出,即
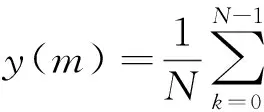
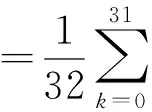
(28)
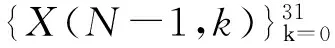
Matlab软件是一种64位浮点计算引擎,并给出十进制数的结果[9],一般短期内不会因为有限字长效应出现输出不稳定现象。而现有数字信号处理(DSP)器件或现场可编程门阵列(FPGA)器件上采用有限字长(字长为8 bit,12 bit等)的定点或浮点二进制运算则可能出现输出不稳定现象,因此,需要用Matlab仿真有限字长的定点或浮点二进制运算。仿真时需要对输入数据、各种运算参数及中间结果均做量化处理,并对乘法运算结果做量化舍入处理后,研究有限字长对滑动DFT算法输出稳定性的影响。本文仿真时取字长b=8 bit的定点运算单元。
仿真时,将不作量化和舍入处理的滑动DFT算法的输出结果作为理想输出,与经过量化和舍入处理的滑动DFT算法输出结果,以及与经过量化和舍入处理并经过LMS算法(文献[4]中介绍的算法)改造后的滑动DFT算法输出结果,还有与经过量化和舍入处理并经过改进Goertzel算法改造后的滑动DFT算法(图3(b)频率单元)输出结果,进行比较,如图5所示,图中横坐标代表时间序列m.
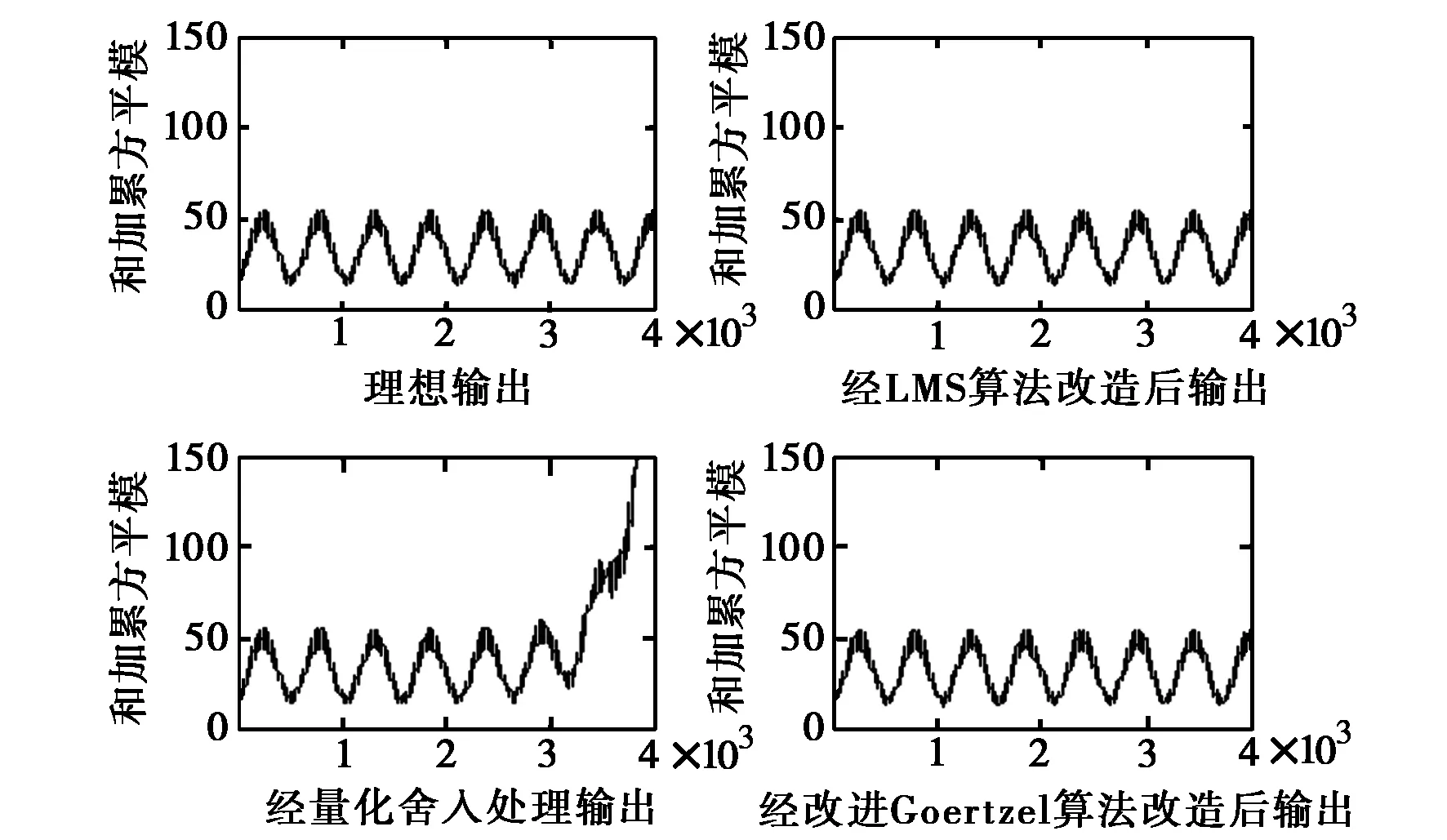
图5 经过不同处理后的滑动DFT输出结果比较
在图5中,经过量化和舍入处理的滑动DFT算法输出结果随着时间的推移,出现了"漂移现象"(误差积累导致失稳)。而经过量化和舍入处理并经过LMS算法改造后的滑动DFT算法输出结果,与经过量化和舍入处理并经过改进Goertzel算法改造后的滑动DFT算法输出结果,都不会出现"漂移现象",可以长时间连续分析信号时频谱。但经过改进Goertzel改造后的滑动DFT算法,与经过LMS算法改造后的滑动DFT算法比较,计算量更少,控制逻辑更简单。
6 结 论
由改进Goertzel算法的递归单元对逐点滑动DFT算法的频率单元改造后,改进滑动DFT算法的频率单元不会出现输出不稳定现象,这种方法在连续实时频谱分析中具有重要的意义。
由于时域加窗(指非矩形窗)会破坏数据帧滑动的连续性,致使滑动DFT算法的时域差分方程不再成立,需要在频域加窗,以减少频谱泄露。关于频域加窗代替时域加窗,以减少频谱泄露方面的内容,可以参考文献[1-4],本文不再赘述。
[1] JACOBSEN E, LYONS R. The sliding DFT[J] . IEEE Signal Processing Magazine, 2003, 20(3): 74-80.
[2] JACOBSEN E, LYONS R. An update to the sliding DFT[J]. IEEE Signal Processing Magazine, 2004, 21(1): 110-111.
[3] FARHANG-BOROUJENY B, GAZOR S. Generalized sliding FFT and its application to implementation of block LMS adaptive filters[J]. IEEE Transactions on Signal Processing, 1994, 42(3): 532-538.
[4] BEAUFAYS F, WIDROW B. On the advantages of the LMS spectrum analyzer over the nonadaptive implementations of the sliding-DFT[J]. IEEE Transaction on Circuits and Systems I: Fundamental Theory and Applications, 1995, 42(4): 218-220.
[5] 王宏伟, 赵国庆. 递归算法的参数设置[J].电波科学学报, 2010, 25(6): 1187-1190.
WANG Hongwei, ZHAO Guoqing. Parameter setting of recursive algorithm[J]. Chinese Journal of Radio Science, 2010, 25(6): 1187-1190. (in Chinese)
[6] 胡广书. 数字信号处理——理论、算法与实现[M]. 北京: 清华大学出版社, 2003.
[7] GERALD G.An algorithm for the evaluation of finite trigonometric series[J]. The American Mathematical Monthly, 1958, 65(1): 34-35.
[8] BANKS K. The Goertzel algorithm[J]. Embedded System Programming, 2002, 15(9): 32-42.
[9] 维纳 K 恩格尔, 约翰G普罗克斯. 数字信号处理(使用MATLAB)[M]. 刘树棠, 译. 西安: 西安交通大学出版社, 2002.

