卫星遥感资料在蒸发波导数值预报中的应用

王振会 杨 璐 姚展予 王 喆

(1.南京信息工程大学气象灾害省部共建教育部重点实验室,江苏 南京 210044; 2.南京信息工程大学大气物理学院,江苏 南京 210044; 3.中国气象科学研究院,北京 100081;4.中国气象局培训中心,北京 100081)

引 言

蒸发波导[1]预报很重要,其主要参数是蒸发波导高度,它表明了蒸发波导的厚度和强度。通常确定蒸发波导高度的方法有直接测量法、微波传播法和雷达探测法,但这些方法都无法满足人们对大范围海区蒸发波导环境时空分布的需求[2]。

数值天气预报中尺度模式已具有较高的垂直分辨率,能够对近地层的中尺度现象进行数值预报与模拟,在模式中加入卫星遥感资料,能大大提高模式初始场质量,从而能够对近地层的中尺度现象进行更好的数值预报与模拟[3]。现代卫星遥感技术可提供全球海面上高分辨率的温度、风速和风向、热带降水等一系列大气特征量的观测数据[4],其中,海面温度是研究海面水汽和热量交换的一个重要物理参数,而海面风场几乎与所有的海水运动直接相关。这些具有高时空分辨率的卫星遥感数据为研究大范围海域的蒸发波导环境实时变化、季节和气候变化提供了基础。

在国内,王振会等[5]利用天气预报模式(WRF),对发生在黄淮江淮流域的一次大气波导过程进行了数值模拟与对比分析,发现WRF模式可以反映出大气边界层内的逆温和湿度锐减并较好地模拟大气波导的变化。胡晓华等[6]利用有限区域预报模式(ARPS)对一次受台风影响的大气波导过程进行了分析和数值模拟,认为对大气波导进行数值模拟时,初始场十分重要,同化多个测站探空资料的数值模拟表明ARPS模式对大气波导具有一定的预报能力。成印河等[7]利用中尺度气象预报模式(MM5)对大气波导进行了数值模拟的研究,认为MM5模式不仅能够模拟海上大气波导的发生,而且可定量描述低空大气波导参数的三维空间变化。陈莉等[8]利用MM5模式对2007年中国近海大气蒸发波导进行了全年的高分辨的数值模拟,详细分析了蒸发波导的季节分布特征及其与海洋环流和海面气象条件的相关关系。

在国外,由美海军研究实验室(NRL)开发研制的海洋大气耦合中尺度预报系统(COAMPS)已经投入业务使用,其功能之一就是预报蒸发波导高度,评估大气环境对电磁波传播的影响。Burk和Thompson[9]采用美国海军业务化区域大气预报系统(NORAPS)对1993年8月23日～9月3日期间太平洋东部沿岸地区的大气折射率作了24 h的滚动预报试验,结果表明:中尺度大气数值预报模式能预报海岸地区大气折射率的日变化及天气系统,如海陆风环流等对大气折射率的影响,只是预报的大气波导特征量与实际还存在一定的差距。

利用WRF中尺度数值模式及其三维变分同化系统,同化海面风和海面温度等卫星遥感资料,将Babin蒸发波导模型与WRF模式耦合,建立了一个海洋蒸发波导预报模式,并用于研究2002年5月25～26日在福建省平潭岛地区的一次蒸发波导过程。

1 海洋蒸发波导高度的确定

蒸发波导高度是表征海洋上蒸发波导强度的重要参数,也是确定蒸发波导对电磁波传播影响的一个重要参量。目前国内外确定蒸发波导高度的模式有多种,包括LKB (Liu-Katsaros-Busin)蒸发波导模式[15]、MGB(Musson-Genon、Gauthier、Bruth)蒸发波导模式[10]、Babin蒸发波导模式[11]等。其中,Babin模式使用了在热带海洋全球大气海气耦合响应试验(TOGA COARE)中提出的描述海洋大气边界层物理过程的最新技术,他认为该模式优于P-J和MGB两种模式。本文采用Babin基于通量算法的新模型来计算蒸发波导高度,加入张强等[12]提出的通量廓线关系,从而将莫宁-奥布霍夫(M-O)理论[13]拓展到甚低风速条件下和近岸沿海地区。

对于微波波段,大气折射指数表达式为

(1)

式中:A=77.6 K/hPa;B=4 810 K2/hPa;p是气压(单位:hPa);e是水汽压(单位:hPa);T是气温(单位:K)。Babin模式使用的M-O相似变量是位温和比湿这两个保守量,借助于位温θ和比湿q与p、T、e的关系[11],并利用静力平衡方程,可得

(2)

根据M-O相似理论中位温θ和比湿q的垂直梯度表达式[13]并令温度和湿度的普适函数Φt、Φq相等,由式(2)可得

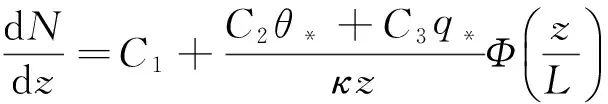
(3)

式中:θ*、q*为特征尺度参数;L为M-O长度。当式(3)等于形成波导的临界值-0.157 m-1时,所对应的高度z就是波导高度zd,所以

(4)

式中温度和湿度的普适函数Φ在中性、稳定条件下以及不稳定条件下分别为

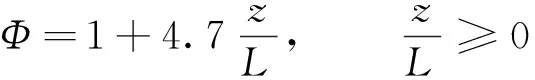
(5)

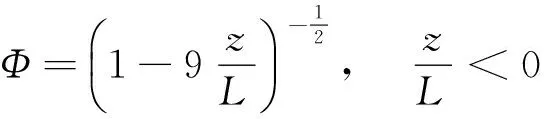
(6)

为了从式(4)解得蒸发波导高度zd, 需要计算θ*、q*和L,可根据文献[14]和[15]提出的算法来确定。

2 个例、资料与模式参数简介

2002年5月25日,福建省平潭岛附近海域发生一次蒸发波导,将平潭岛铁塔传感器测量的近地层大气温、湿、压、风、海表水温等代入Babin模式中计算得到的蒸发波导高度称为“观测结果”。对这次蒸发波导进行基于WRF模式的模拟预报试验,采用当日00:00(UTC)NCEP的全球客观分析场全球分析(FNL)资料作为初始场,进行直到次日00:00的24 h模拟预报。将利用WRF模式预报输出的温、压、湿、风、海表水温数据代入Babin模式中得到蒸发波导高度的“预报结果”。

FNL资料格点分辨率1°×1°,属于全球预报系统(GFS)并经过再分析而生成的产品。本文同化的海面风和海表温度资料分别来自于“快速测风”(QuickSCAT)卫星和日本静止气象卫星(GMS5),水平分辨率分别为0.25°×0.25°,0.1°×0.1°.

WRF模式是美国最新的中尺度区域模式,水平分辨率设为30 km,模拟区域中心为25°N、119°E,垂直分41层[8]。物理过程包括延世大学(YSU)[16]边界层过程、KF(Kain-Fritsch)方案[17]、天气预报单时刻3类简单冰方案积云对流微物理过程[18]、辐射传输模式(RRTM)长波辐射方案,Dudhia短波辐射方案[8]。WRF模式提供了基于变分技术的数据同化模块,用以同化常规观测、雷达、卫星等各种数据以改善初始场。

3 数值模拟试验及结果分析

3.1 试验方案

为了对比资料同化对初始场和预报结果的影响,设计了4种试验方案进行对比分析:

1) 模式不加以下任何一种可同化资料,积分24 h;

2) 同化25日00∶00的海面风资料,积分24 h;

3) 同化25日00∶00的海表温度资料,积分24 h;

4) 同时同化25日00∶00的海面风资料和海表温度资料,积分24 h.

3.2 模拟结果分析

3.2.1 同化对初始场的影响

计算蒸发波导只需要近地层一层的气象数据,所以下面仅分析近地层10 m高度处同化对初始场的影响,如图1所示。

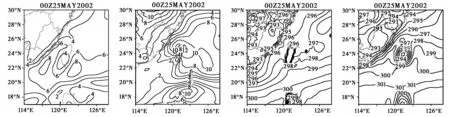
(a) QuickSCAT风场 同化前的初始风场 (b) QuickSCAT风场 同化后的初始风场 (c) GMS5海表温度同化 前的海表温度初始场 (d) GMS5海表温度同化 后的海表温度初始场图1 2002年5月25日00:00资料同化对初始场的影响

图1(a)与(b)分别表示同化前、后的10 m高度处风场。可见,同化前,南海地区强风速区的速度最大值分别位于点(117.5°E,22.5°N)及(122°E,21.5°N)附近,最大值为8;同化后,强速度区向东北方向偏移,速度最大值增大到12,位于(122°E,24.5°N)附近。同化后，风场速度中心发生了偏离,且中心数值最大值增大。

图1(c)与(d)分别为同化前与同化后的海表温度图。对比可见,同化海表温度之后对海面上的温度影响较大。其中,在台湾岛以北的海域内,同化后温度上升了2～3 ℃,而在台湾岛以南的大面积海域经同化,温度普遍升高了1 ℃.

3.2.2 蒸发波导高度预报结果对比分析

将在4种试验方案下WRF每小时一次预报输出的海面大气温、湿、压、海表水温、海面风速等参量分别代入Babin模式中,计算得到25日00∶00～26日00∶00连续24 h的蒸发波导高度。因篇幅所限,仅给出25日00∶00的4种方案下的WRF预报结果,如图2所示,4种方案下的预报结果均呈现出东南沿海地区蒸发波导的发生,在模拟的初始时刻,未同化任何观测资料的蒸发波导高值区主要位于西南象限,高度达到22 m以上;其他3种方案下的蒸发波导高度高值区主要位于西北象限,高度最大值增加,达到24 m以上。随着时间的推移,4种方案下的蒸发波导高度都不断降低,26日00∶00已经降到18 m以下。

为了定量比较4种方案下WRF的预报结果,用平潭岛站(119.78°E,25.52°N;图2(d)中点P处)蒸发波导高度的观测结果分别与4种方案下的模式预报值进行对比,如图3所示。其中黑实线表示铁塔观测值,其他线分别表示不同试验方案下的模式预报值。

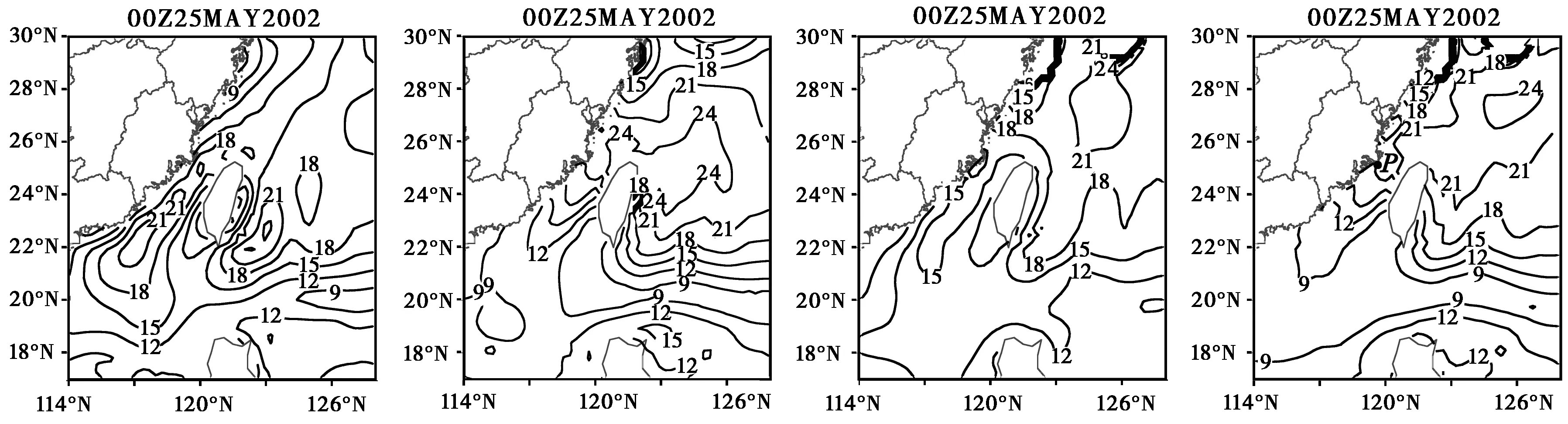
(a) 第1种方案 (b) 第2种方安 (c) 第3种方案 (d) 第4种方案图2 2002年5月25日00∶00的4种试验方案下WRF模式预报的蒸发波导高度结果图

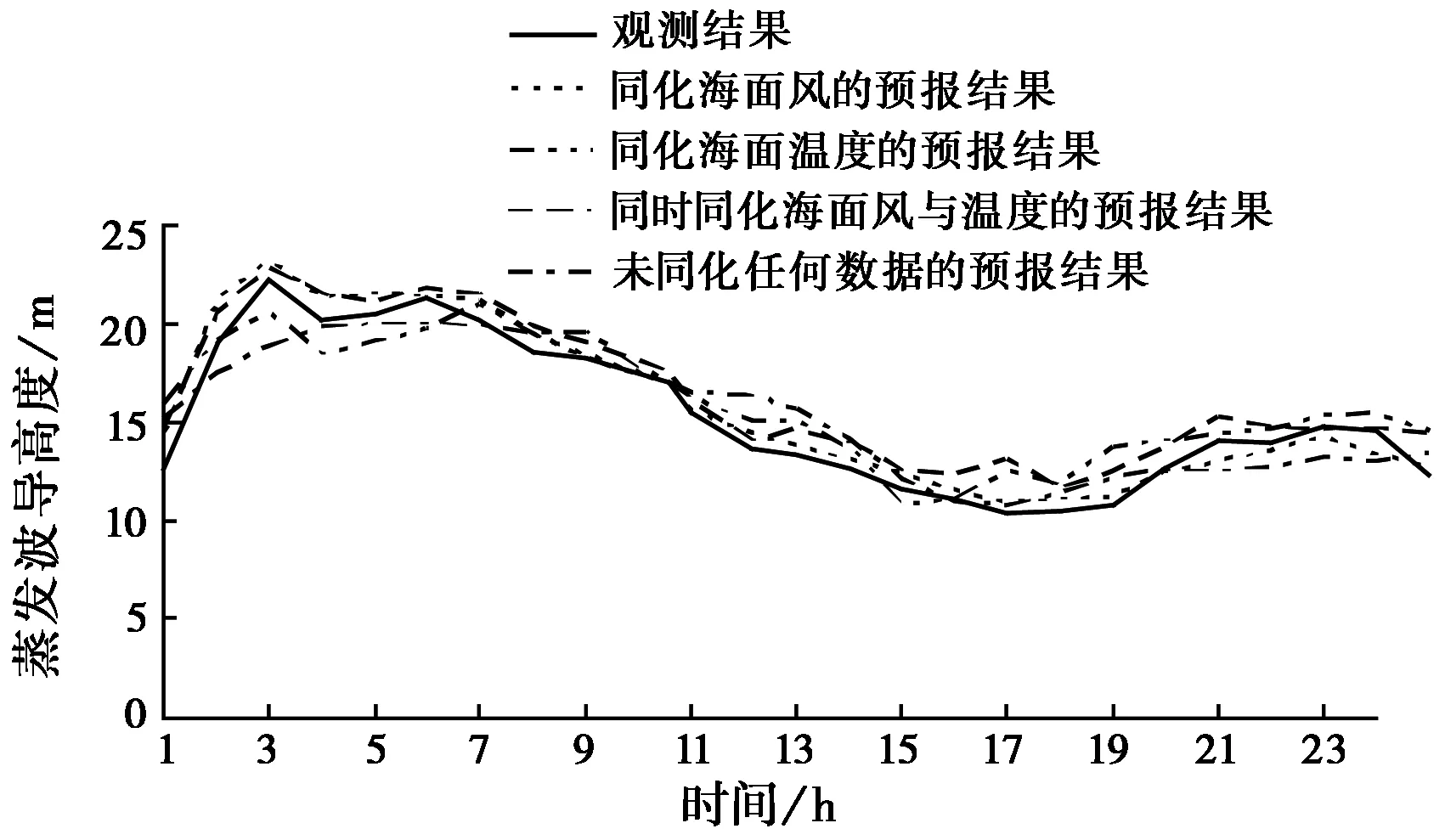
图3 2002年5月25日00:00～26日00:00的种方案下平潭岛蒸发波导高度预报与观测对比(其中横轴1 h表示25日00:00,其余类推)

用Xi和Yi分别代表模式预报结果与观测结果的蒸发波导高度值,“Xi-Yi”为预报误差。分别计算4组预报值的误差均方根(RMS)、无偏误差均方根(RMS′)以及相关系数rXY[19]。结果如表1所示。

表1 平潭岛蒸发波导高度的预报结果统计量

从图3和表1可以看出：本模式方法预报值与观测值变化规律基本一致(4种方案下相关系数都在0.92以上),但同化遥感资料有助于提高相关系数;“同时同化海表风和海面温度”情况下,经过偏差订正后的预报效果最好(表中RMS′最小)。单独同化海面风或海面温度资料都会改善预报结果,但单独同化海面温度不如单独同化海表风场。

模式预报的波导高度总体上都比实测计算值偏高。海面微气象条件如近地层大气温度、湿度、气压、风向风速、海表水温对蒸发波导的高度具有决定作用。陈莉等[8]指出,相比海温而言,海气温差和海面风速对波导高度的影响较大,海气温差与波导高度呈负相关,海面风速与之呈正相关。穆均[20]利用南海6个岛屿站对NCEP再分析风场资料按五年、季节进行统计分析,结果显示:NCEP风速比西沙、南沙、珊瑚岛和东沙实测风速都偏大。所以,模式中所采用的风向风速资料相比铁塔传感器实测资料值相对偏大,这在一定程度上造成了模式预报的波导高度总体上都比实测计算值偏高。

对于缺少观测资料的海洋,同化散射计风场资料和GMS5海面温度资料可以明显改善模式初始场,对于低层风场和海面温度有一定的调整。其中,第二组同化方案对预报效果改善最为明显,这主要是由于QuickSCAT散射计风场的反演不仅使用了SeaWinds探测数据,还应用了数值天气预报资料(NWP)和专用传感器微波成像仪(SSM/I)或热带降雨测量卫星(TRMM)等的多通道微波探测资料以及海陆模式,是多种资料综合应用的结果。虽然散射计风场资料同化对于质量场以及中高层垂直结构的影响有限,但对于低层风场调整比较大,而本文中所需要的是近地层的海面风场,所以它对于海面风初始场的优化效果非常明显。可见,同化遥感资料对于本模式方法的蒸发波导高度预报是有帮助的。

4 结论与分析

本文以WRF模式为基础,通过WRF3D-VAR变分同化系统将海面风速、海面温度资料等卫星遥感资料同化,然后耦合Babin蒸发波导模式,构建了一个海洋蒸发波导预报模式,并用于模拟了2002年5月25日00:00至26日00:00(UTC)福建省平潭岛附近海域的一次蒸发波导过程,比较了卫星遥感海面风和海面温度资料的同化对模式初始场和其后24 h蒸发波导高度预报的影响,经与平潭岛铁塔观测数据对比表明：卫星遥感资料同化可以使模式初始场优化,有助于改善预报结果,蒸发波导高度的24 h之内模式预报结果与铁塔观测值结果变化规律基本一致。

虽然本次福建平潭岛地区蒸发波导数值预报的高度与观测数据有着较好的一致性,但是由于广大海洋地区缺少高时空分辨率的观测资料,可供对比分析的实测资料较少,所以对于大片海域蒸发波导高度的验证无法实现,数值模拟区域蒸发波导的可靠性尚需进一步验证和改进。

致谢：感谢潘维玉老师、韩丰同学等在研究工作中的帮助，感谢福建省平潭岛气象局在一些资料获取上的大力支持。

[1] 姚展予, 赵柏林, 李万彪, 等. 大气波导特征分析及其对电磁波传播的影响[J]. 气象学报, 2000, 58(5): 605-615.

YAO Zhanyu, ZHAO Bolin, LI Wanbiao, et al. The analysis of characteristics of atmospheric duct and its effect on the propagation of electromagnetic wave[J]. Scientia Meteorologica Sinica,2000, 58(5): 605-615. (in Chinese)

[2] 成印河. 海上低空大气波导的遥感反演及数值模拟研究[D]. 北京: 中国科学院研究生院, 2009.

CHENG Yinhe. A study on atmospheric ducts over the sea retrieval with AMSR-E satellite data and its numerical simulation[D]. Beijing: Chinese Academy of Sciences, 2009. (in Chinese)

[3] 陈 莉, 高山红, 康士峰, 等. 中国近海大气波导的时空特征分析[J]. 电波科学学报, 2009, 24(4): 702-708.

CHEN Li, GAO Shanhong, KANG Shifeng, et al. Statistical analysis on spatial-temporal features of atmospheric ducts over Chinese regional seas[J]. Chinese Journal of Radio Science, 2009, 24(4):702-708. (in Chinese)

[4] MENG Lei, He Yijun, WU Yumei, et al. Neural network retrieval of ocean surface parameters from SSM/I data[J]. Mon Wea Rev, 2007, 135(2): 586-597.

[5] 王振会, 王 喆, 康士峰, 等. 利用WRF模式对大气波导的数值模拟研究[J]. 电波科学学报, 2010, 25(5): 913-919.

WANG Zhenhui, WANG Zhe, KANG Shifeng, et al. Numerical simulation of atmospheric duct process with WRF model[J].Chinese Journal of Radio Science, 2010, 25(5): 913-919. (in Chinese)

[6] 胡晓华, 费建芳, 张 翔, 等. 一次大气波导过程的数值模拟[J]. 气象科学, 2008, 28(3): 294-300.

HU Xiaohua, FEI Jianfang, ZHANG Xiang, et al. Numerical simulation of an atmospheric duct[J]. Scientia Meteorologica Sinica, 2008, 28(3): 294-300. (in Chinese)

[7] 成印河, 赵振维, 何宜军, 等. 大气波导过程数值模拟研究[J]. 电波科学学报, 2009, 24(4): 259-263.

CHENG Yinhe, ZHAO Zhenwei, HE Yijun, et al. Numerical simulation of atmospheric duct process[J]. Chinese Journal of Radio Science, 2009, 24(4): 259-263. (in Chinese)

[8] 陈 莉, 高山红, 康士峰, 等. 中国近海蒸发波导的数值模拟与预报研究[J]. 中国海洋大学学报, 2011, 41(1/2): 1-8.

CHEN Li, GAO Shanhong, KANG Shifeng, et al. Numerical modeling and forecasting of evaporation ducts over China seas[J]. Journal of Ocean University of China, 2011, 41(1/2): 1-8. (in Chinese)

[9] BURK S D, THOMPSON W T. Mesoscale modeling of summertime refractive conditions in the Southern California Bight[J]. J Appl Meteor, 1997, 36(1): 23-31.

[10] MUSSON-GENON L, GAUTHIER S, BRUTH E.A simple method to determine evaporation duct height in the sea surface boundary layer[J]. Radio Science, 1992, 27(5): 635-644.

[11] BABIN S M, YOUNG G S, CARTON J A. A new model of the oceanic evaporation duct[J]. J Appl Meteor, 1997, 36(3): 193-204.

[12] 张 强, 胡隐樵. 热平流影响下湿润地表的通量廓线关系[J]. 大气科学, 1995, 19(1): 8-20.

ZHANG Qiang, HU Yinqiao. The flux-profile relationships under the condition of heat advection over moist surface[J]. Chinese Journal of Atomspherica Sciences, 1995, 19(1): 8-20.

[13] OBUKHOV A. Turbulence in an atmosphere with a non-uniform temperature[J]. Boundary-Layer Meteorol, 1971, 2(1): 7-29.

[14] FAIRALL C W, BRADLEY E F, ROGERS D P, et al. Bulk parameterization of air-sea fluxes for tropical ocean-global atmosphere coupled-ocean atmosphere response experiment[J].J Geophys Res, 1996, 101(C2): 3747-3764.

[15] LIU W T, KATSAROS K B, BUSINGER J A. Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface[J]. J Atmos Sci, 1979, 36(9): 1722-1735.

[16] HONG S Y, NOH Y, DUDHIA J. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 2006, 134(9): 2318-2341.

[17] 伍华平, 束 炯, 顾 莹, 等. 暴雨模拟中积云对流参数化方案的对比试验[J]. 热带气象学报, 2009, 25(2): 175-180.

WU Huaping, SHU Jiong, GU Ying, et al. The effects of different cumulus parameterization schemes in WRF on heavy rainfall in Hunan province[J]. Journal of Tropical Meteorology, 2009, 25(2): 175-180. (in Chinese)

[18] 胡向军, 陶健红, 郑 飞, 等. WRF模式物理过程参数化方案简介[J]. 甘肃科技, 2008, 24(20): 73.

HU Xiangjun, TAO Jianhong, ZHENG Fei, et al. Introduction of Physical processes parameterization schemes in WRF model[J]. Gansu Science and Technology, 2008, 24(20): 73. (in Chinese)

[19] 吴诚鸥, 秦伟良. 近代实用多元统计分析[M]. 北京: 气象出版社, 2007.

[20] 穆 均. NCEP再分析资料与南海岛屿测站资料风场对比分析[J]. 气象水文装备, 2010, 21(1): 45-48.

MU Jun. Contrast and analysis between NCEP reanalysis data and observation data of wind field in South China Sea[J]. Meteorological and Hydrological Equipments, 2010, 21(1): 45-48. (in Chinese)