CMAC与大林的复合控制在纯滞后系统中的应用

高小凤，李 虹

（太原科技大学 电子信息工程学院，山西 太原 030024）

大多数工业过程中，例如锅炉温度控制过程，造纸、化工过程控制等，其控制系统一般为纯滞后系统，纯滞后性质会使系统的过渡过程时间加长、产生大幅度的超调，从而使控制品质变差，甚至会影响稳定性。因此对于纯滞后系统，人们期望克服大惯性大时滞对控制系统的不利影响，从而改善控制质量。长期以来人们做了大量的研究，例如：PID算法、大林算法、史密斯补偿法、智能控制算法等。

大林算法一般用于含有纯滞后的控制问题中，它相较于常规的控制方法，能够改善超调问题，但其调节时间相对较长，在实际中应用不太理想。文中将小脑模型神经网络（CMAC）与大林算法相结合，可以很好地改善控制品质，提高响应速度，达到控制要求。

1 CMAC和大林算法的复合控制

1.1 大林算法的基本原理

对于大部分工业控制系统，常规的计算机控制系统结构图如图1所示。其中为控制器，为纯滞后控制对象。

而对于被控制对象都是带有纯滞后的一阶或二阶惯性环节，现以一阶惯性环节为例阐述大林算法的设计。

图1 计算机控制系统结构图Fig.1 Computer control system structure

设定一阶惯性环节的传递函数为：

期望闭环传递函数为：

式中，K为放大系数，τ为纯滞后时间，T为纯滞后时间常数。T0为闭环系统期望的时间常数；τ0为纯滞后时间；t为采样周期，其中在设计中纯滞后τ0为采样周期T的整数倍。具体设计步骤如下[1]：

1）期望闭环传递函数 φ（s）和被控对象 G（s）的离散化

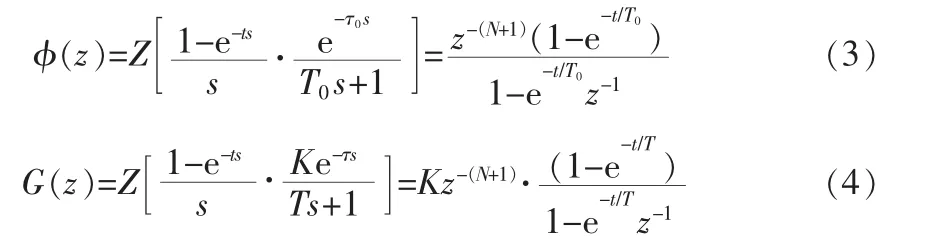
2）求取控制器 D（z）

利用以上方法可在MATLAB环境下对大林算法进行编程及在SIMULINK中仿真程序的设计。

但大林算法存在一定的缺陷，如果所设计的控制器在左半平面有极点时，容易产生振铃现象，振铃现象使得控制器的输出产生衰减震荡，容易磨损执行机构。如果在有交互作用的多参数控制系统中，振铃现象还可能影响到系统的稳定性，所以消除振铃很必要。

消除振铃的方法是令控制器中振铃因子中的z为1。

1.2 CMAC的基本原理

CMAC小脑神经网络是一种联想网络，对每一输入只有少部分神经元与之有关，它的联想具有局部泛化能力。从总体讲，CMAC网络表示一种非线性映射，其学习算法采用简单的δ算法[2]，学习速度快，适合于实时控制。

CMAC的结构图如图2所示，它是前馈网络，有概念映射和实际映射两个基本映射，表示输入/输出之间的非线性关系。

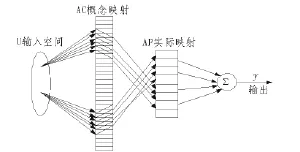
图2 CMAC结构图Fig.2 CMAC structure

1）概念映射

概念映射（Conceptual Mapping）是从空间U至概念存储器AC的映射。

设 n 维输入向量为：u=[u1，u2，…，un]T，量化编码为[u]后，映射至AC中c个存储单元，c也称为泛化参数，它规定了网络内部影响网络输出的区域大小。

2）实际映射

实际映射（Practical Mapping）是指由概念存储器AC的c个单元用杂散编码技术映射至实际存储器AP的c个单元。c个单元中存放相应的权值，则网络的输出为AP中c个单元的权值的和[3-4]。

1.3 CMAC和大林的复合控制算法

CMAC常规的控制结构一般有两种：直接逆模型运动控制和前馈控制。本文与大林算法的结合采用前馈控制，由大林控制实现闭环反馈控制，从而能保证系统的稳定性，也能提高系统的响应速度。CMAC与大林复合控制结构如图3所示。

该系统的控制算法为：

式中 ud（k）、un（k）分别为大林控制器的输出和 CMAC 的输出；αi为二进制选择向量；c为CMAC网络的泛化参数；u（k）为复合控制器的输出。

CMAC的学习算法为：

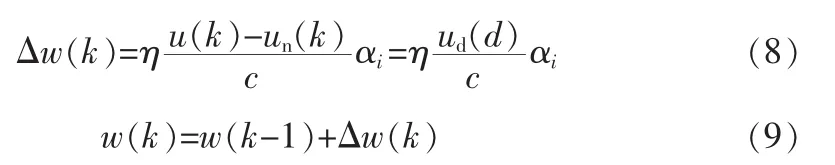
式中η为网络学习效率，一般取η∈（0，1）。

每进行一个控制周期，就会计算出相应的CMAC的输出un（k），同时于总控制器输出 u（k）对比，修正权值，进行学习，其目的是使输出之差最小。经过CMAC学习，使得系统的总控制输出由CMAC产生[5-7]。

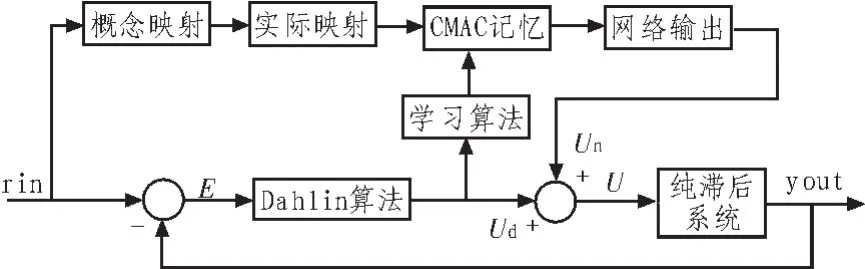
图3 CMAC-大林复合控制结构图Fig.3 CMAC-Dahlin composite control structure

2 纯滞后系统仿真应用

首先在MATLAB中对大林算法编写M文件程序，通过计算，可知大林算法应用在该系统中有严重的振林现象，需消除振铃因子。式子（10）为消除振铃因子的大林控制器表达式。该式子可用于SIMULINK环境下大林控制器的设计。

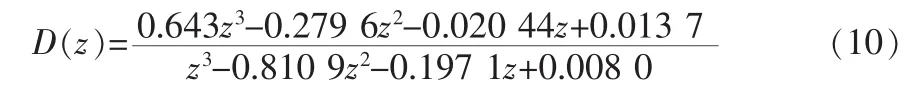
然后将大林算法与CMAC相结合编写M文件进行仿真，系统单位阶跃响应曲线仿真结果如图4（a）、（b）所示。

图4 不同算法的单位阶跃响应曲线对比图Fig.4 Contrast figure step responses of different algorithms

通过仿真结果可以看出，系统加入CMAC后控制效果比大林算法控制效果要好得多，加快了控制响应速度，充分的体现了CMAC学习速度快的特点。

图4仅在M文件中进行仿真，其控制算法不能直接应用于实时仿真，为增强算法的实用性故将这些算法编写成功能模块，并运用在SIMULINK环境中进行仿真，鉴于在SIMULINK环境可进行实时控制，从而增强了控制算法的实用性。SIMULINK坏境下控制系统仿真结构如图5所示。图中在编写在CMAC控制模块中，利用时钟Clock功能实现神经网络权值的初始化。

图5 大林和CMAC-大林控制器的仿真结构图Fig.5 Dahlin and CMAC-Dahlin controller simulation structure

图6为控制系统的仿真结果。由以上仿真波形给出了不加控制算法的系统的输出波形以及分别加入大林、CMAC—大林算法后系统的输出波形。可以看出，大林控制器能够很好地抑制超调，达到控制要求，但调节时间较长；CMAC—大林控制器不仅能够减少超调，而且提高了响应速度，使系统能够实现良好的控制品质。对比所得波形，同时也验证了在SIMULINK中仿真的正确性，从而可以将这种控制方法运用在实际的纯滞后系统中进行实时控制。

图6 仿真波形Fig.6 Simulation wave

3 结束语

采用大林算法和小脑神经网络相结合的复合控制，对纯滞后系统进行仿真控制。相应的给出了控制器结构和M文件的控制算法以及结果，为了能将控制算法更好的应用在实际系统中，本文将其转换到SIMULINK中实现设计、仿真。通过仿真可以达到很好的控制效果，同时也体现了CMAC—大林复合控制器具有了两种算法的优点，能实现良好的控制品质。

[1]朱苏朋，符文星，杨军.计算机控制系统及仿真[M].北京：国防工业出版社，2009.

[2]刘叔军，盖晓华.MATLAB7.0控制系统应用与实例[M].北京：机械工业出版社，2006.

[3]徐丽娜.神经网路控制[M].北京：电子工业出版社，2003.

[4]刘金锟.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2004.

[5]阮晓钢，陈石，左国玉，等.基于Dahlin算法的CMAC控制器设计[J].控制工程，2007，14（3）：287-289.RUAN Xiao-gang，CHEN Shi，ZUO Guo-yu，et al.CMAC controller based on Dahlin algorithm for time-delay systems[J].Control Engineering of China，2007，14（3）:287-289.

[6]文定都.针对纯滞后系统神经网络Dahlin控制的研究[J].自动化仪表，2008，29（12）：38-43.WEN Ding-du.Research on neural network Dahlin control for dead time system[J].Process Automation Instrumentation，2008，29（12）:38-43.

[7]邢东峰，董海鹰.遗传小脑神经网络在液位控制中的应用[J].计算机测量与控制，2006，14（9）：1198-1199.XING Dong-feng，DONG hai-ying. Cerebella model articulation controller based on genetic algorithm applied in liquid level control[J].Computer Measurement&Control，2006，14（9）:1198-1199.