采用主成分分析法寻求重金属污染源位置

白春阳,王琪媛,吴世琴,武广伟

（河南科技学院,河南新乡453003）

采用主成分分析法寻求重金属污染源位置

白春阳,王琪媛,吴世琴,武广伟

（河南科技学院,河南新乡453003）

针对寻找重金属污染源的位置问题,利用标准差体现数据离散程度的性质,对重金属元素的分布情况进行分析,并运用主成分分析法,建立了一个确定污染源的数学模型.通过对收集数据的处理,可以方便而快捷地找出重金属污染源.

重金属污染；标准差；主成分分析法；污染源

随着城市经济的快速发展和人口的不断增加,人类活动所造成的环境污染也越来越严重,对人类的生活质量带来了显著的影响.准确地分析出各城区重金属污染的主要原因,并寻求出污染源的确切位置,对于政府及相关部门采取相应的治理措施具有至关重要的作用.目前,方便且准确地找出污染源的位置已成为研究的热点[1-7].文献[1]中运用锶同位素,放射性核素示踪技术寻找重金属污染源,不具有普遍的适用性.文献[2]利用半方差函数分析和Kriging最优内插法探索表层土壤重金属污染源,没有得出具体的污染源位置,求解不具体.文献[3]求解污染源的速度较慢,灵活性不够高.为了准确地确定污染源,本文以某城市为例按照不同的功能将城区分为生活区、工业区、山区、主干道路区及公园绿地区等,运用主成分分析法[8-9],通过对其城区土壤地质环境进行调查分析重金属污染物的传播特征建立相应的数学模型,可以快速而又精确地找出污染源的确切位置.

1 问题分析

根据文献[10],整理给出各城区的重金属污染情况,并根据不同地区的实际情况分析和说明重金属在该区域引起污染的主要原因.分析重金属污染物的具体情况,进而由此建立相应的数学模型来确定污染源的确切位置.

2 基本假设

（1）假设文献[10]中所给的数据能客观的反映现实情况,具有可实用性；（2）假设在数据处理过程中的误差忽略不计；

（3）假设每个样本点都能很好地反映该平方公里的实际情况；

（4）假设不考虑人为移动污染源；

（5）假设忽略各重金属元素之间的化学反应.

3 模型的建立与求解

3.1 重金属污染的主要原因

标准差是反映一组数据离散程度最常用的一种量化形式,是表示精密准确的重要指标.常用来衡量一组数据的离散程度,标准差的数值越大,表示该组数据的波动越大,越不稳定.设标准差为σ(x),则有

通过对收集到的数据进行处理,可得到各地区中各元素含量的平均值x,由公式（1）可计算出各地区重金属元素的标准差.比较标准差的大小,进而可得各城区的污染分布的离散程度.土壤中各重金属总量统计结果见表1.

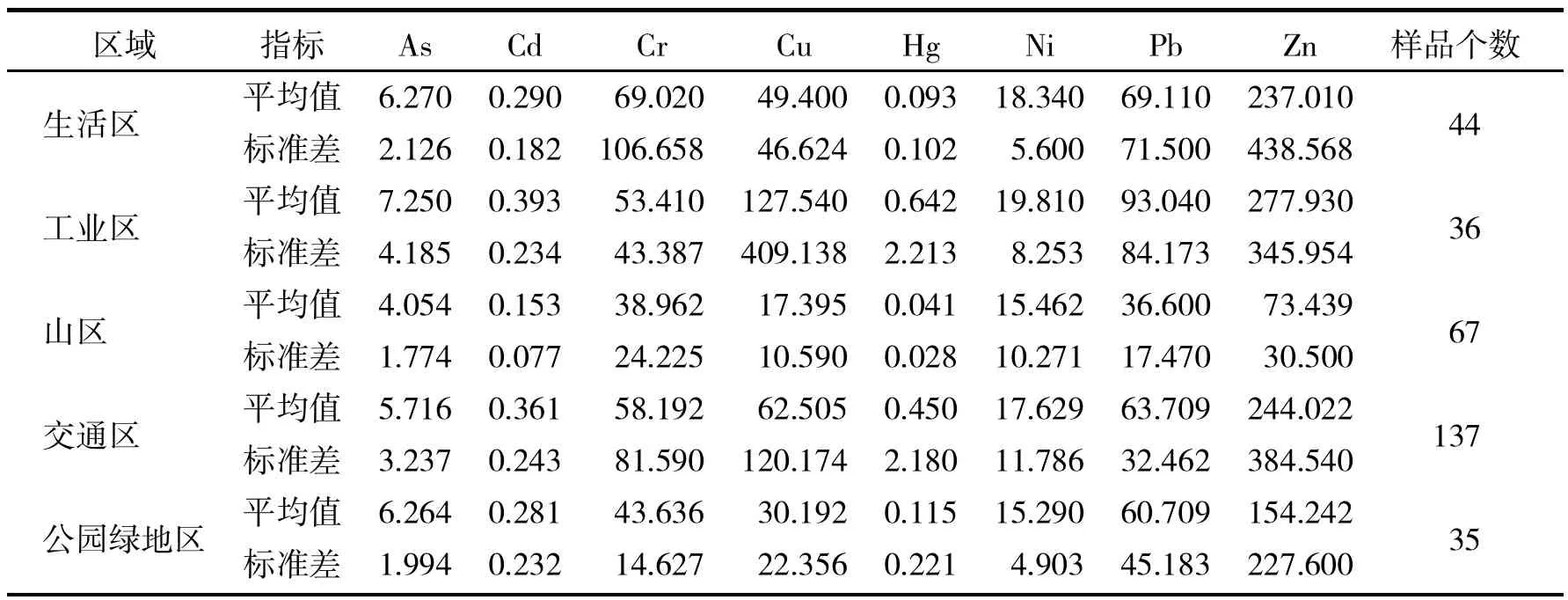
表1 土壤中八种重金属总量统计结果Tab.1 Eight kinds of heavy metals in soil aggregates statisticsμg/g

由表1可知,各功能区域中Zn的总量最高,其平均值排序为工业区（278 μg/g）＞交通区（244 μg/g）＞生活区（237 μg/g）＞公园绿地区（154 μg/g）＞山区（73.4 μg/g）；总体看来,Cr、Cu和Pb的含量较其它元素高出很多,其主要污染因素为矿工业生产排放的“三废”、生活垃圾、道路交通过程中的尾气排放等.

各城区污染严重的主要原因各不相同,生活区主要是区域工业废气沉降,汽车尾气排放,酸雨侵蚀等；工业区主要是当地矿区、化工小企业长期乱排污,生产中燃煤矿产品加工等排放的高浓度烟尘、飘尘、废水和废渣；山区的土壤受人类生产、生活的影响较小,故重金属含量较低；交通区主要受汽车尾气的排放的影响；公园绿地区主要来自于公共垃圾等.

3.2 建立主成分分析模型确定污染源

主成分分析法,也称为主分量分析法,是利用降维的思想,把多指标转化为少数几个综合指标的多元统计分析方法[8-9].当对同一个体进行多项观察时,必定涉及多个线性相关的随机变量,一时难以综合,这时就需要借助主成分分析法来概括诸多信息的主要方面.下面即以主成分分析法建立模型,对8种重金属污染物进行降维,进而来确定污染源.

（1）设有n个样本,每个样本有m个指标,记为

协方差

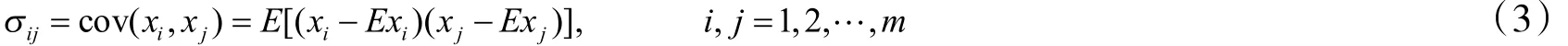
则标准化矩阵为：Z=[Z1, Z2,…,Zm].其中,xi为 重金属整体的测量平均值,x为重金属在各区的测量平均值.

（3）相关系数矩阵为

（4）用相关系数矩阵进行主成分分析,计算R的特征值λi和相应的特征向量ei,i=1,2,…,m.

（5）所选主成分个数的确定

得出主成分的个数s（s≤m）.

为了方便起见我们分别设x1为As,x2为Cd,x3为Cr,x4为Cu,x5为Hg,x6为Ni,x7为Pb,x8为Zn.

根据表1中的重金属含量的标准差数据,运用公式（3）求出协方差矩阵,运用公式（4）求得标准化矩阵,最后由公式（5）得相关系数矩阵,如表2所示.

表28 种重金属元素的相关系数矩阵Tab.2 Eight heavy metal elements of the correlation coefficient matrix

表38 种重金属的载荷矩阵及各主成分解释的方差比例Tab.3 Three Eight kinds of heavy metal matrix and the principal components of variance explained by the proportion

将表3代入公式（7）得出载荷矩阵

得出各样本的4个主成分得分,然后根据需要设定每个重金属的权重,本文选取4个权重相等,即ωi=0.25(i =1,…,4),则F=ω1F1+ω2F2+ω3F3+ω4F4得出各样本点的综合主成分得分F,对其进行排名（取前30名）得表4.注：功能区中1、2、3、4、5分别表示生活区、工业区、山区、主干道路区、公园绿地区.

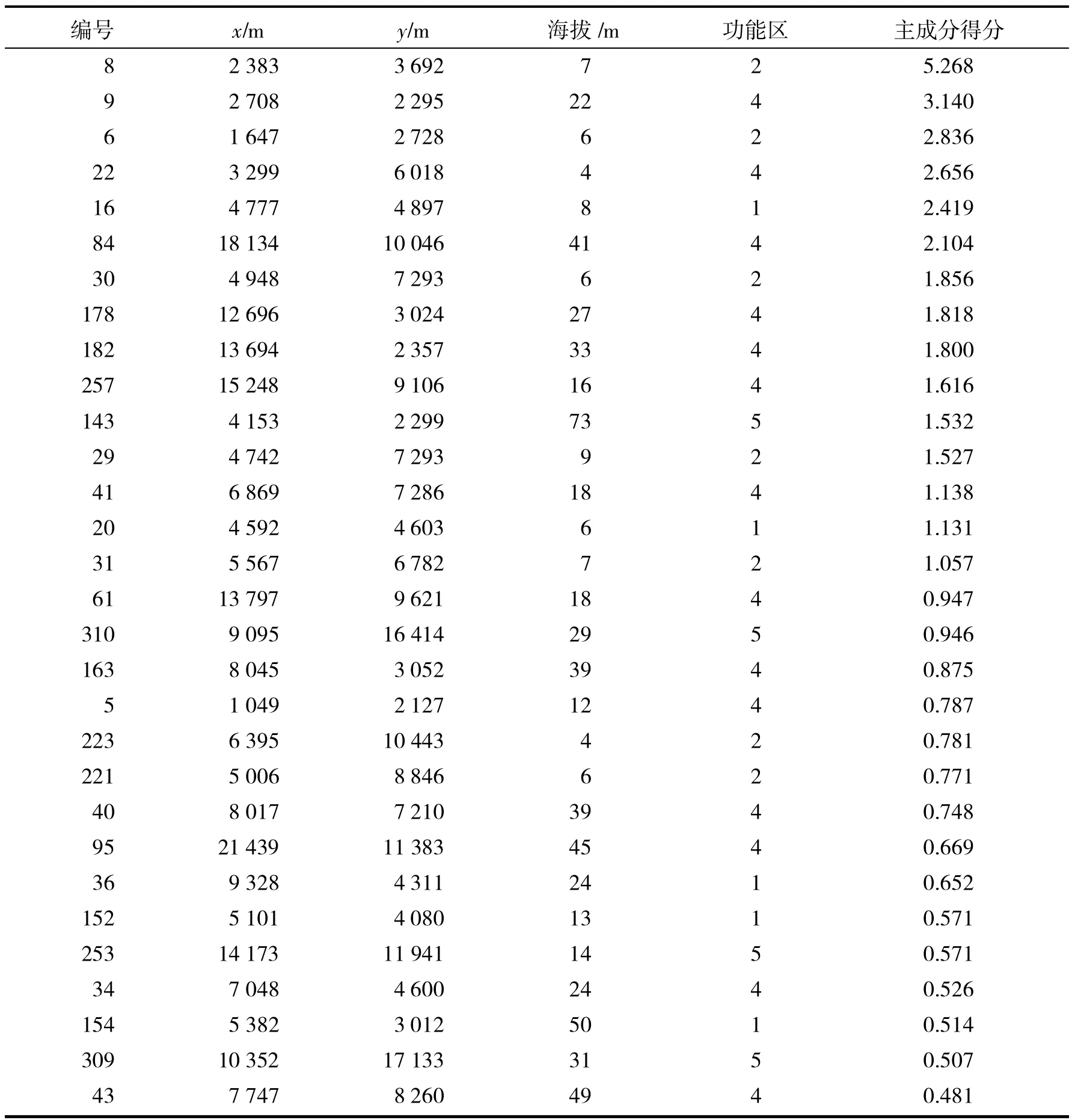
表4 各样本点的综合主成分得分Tab.4 Each sample point comprehensive principal component score

根据表4知道了各样本点的综合主成分得分排名,可以大致确定污染源的位置是编号为：8 9 6 22 16 84 30 178 182 257 143 29 41 20 31,通过查编号可得其具体空间位置.

4 小结

本文针对重金属污染源问题,应用标准差来分析出重金属污染的分布情况,并利用主成分分析法建立数学模型,对重金属污染的污染源位置进行预测.根据所得的主成分得分,可以较为精确地找到污染源的平面坐标位置.不足为模型考虑的范围有限,不易客观准确地确定污染源的具体海拔高度.总体来说利用本方法寻找重金属污染源科学性强,具有普遍实用性.

[1]于瑞莲,胡恭任.土壤中重金属污染源解析研究进展[J].有色金属,2008,60（4）：158-165.

[2]胡克林,张凤荣,吕贻忠,等.北京市大兴区土壤重金属含量的空间分布特征[J].环境科学学报,2004,24（3）：463-448.

[3]姜芝萍,杨俊衡.城市重点污染区土壤重金属污染物评价[J].安全与环境工程,2010（1）：57-64.

[4]陈怀满,郑舂荣.中国土壤重金属污染现状与防治对策[J].人类环境杂志,1999,28（2）：130-134.

[5]段雪梅,蔡焕兴,巢文军.南京市表层土壤重金属污染特征及污染来源[J].环境科学与管理,2010,35（10）：31-35.

[6]黄勇,郭庆荣,任海等.城市土壤重金属污染研究综述[J].热带地理,2005,25（1）：14-18.

[7]Matschullat J,Ottenstein R,Reimann C.Geochemical background-can we calculate it[J].Environmental Geology,2000,39（9）：990-1000.

[8]吴翊,吴孟达,成礼智.数学建模的理论与实践[M].长沙：国防科技大学出版社,1999.

[9]姜启源,谢金星,叶俊.数学模型[M].3版.北京：高等教育出版社,2003：1-12,.

[10]中国工业与应用数学学会.2011年全国大学生数学建模竞赛A题[EB/OL].[2011-12-18].http：//www.mcm.edu. cn/html_cn/node/a1ffc4c5587c8a6f96eacefb8dbcc34e.html.

（责任编辑：卢奇）

Principle components analysis method for the location of heavy metal pollution sources

Bai Chunyang,Wang Qiyuan,Wu Shiqin,Wu Guangwei
（Henan Institute of Science and Technology,Xinxiang 453003,China）

A directed search for heavy metal pollution source location problem,using standard deviation of discrete degree of the data,on the distribution of heavy metals were analyzed,and using the method of principal component analysis,establishes a mathematical model to determine the pollution source,based on the collected data processing, can find the pollution source of heavy metals conveniently and quickly．

heavy metal pollution；standard deviation；principal component analysis；pollution source

O212.4

A

1008-7516（2012）03-0072-05

10．3969/j．issn．1008-7516．2012．03．018

2012-04-11

白春阳（1975-）,女,河南上蔡人,硕士,副教授．主要从事有限元方法及其应用研究．