关于路的并的点可区别V-全染色

马宝林,刘娟,王军涛,丁玉荣

（河南科技学院,河南新乡453003）

关于路的并的点可区别V-全染色

马宝林,刘娟,王军涛,丁玉荣

（河南科技学院,河南新乡453003）

根据简单图的点可区别V-全染色的概念及其染色方法,讨论了m个长度为n的路的顶点不交并的点可区别V-全染色,并给出全色数的结论及其证明,根据结论提出了相应的猜想,为进一步探讨其他简单图的点可区别V-全染色提供了理论证据,丰富了图的点可区别V-全染色的结果.

简单图；全色数；点可区别V-全染色；mPn

图的染色问题是NP完全问题,目前已得到了很多结果[1-3],2004年,张忠辅、陈祥恩等在图的全染色的基础上提出了邻点可区别全染色[1],2008年,又在点可区别正常全染色的基础上提出了图的点可区别一般全染色[2].本文从简单图的点可区别V-全染色的定义出发,讨论mP2、mP3、mP4的点可区别V-全染色,给出全色数的结论及其证明,并提出了自己的猜想.

1 相关概念

在文献[1]和[2]中,对于部分简单图的点可区别正常全染色已有相对完善的结果,并给出定义,图的正常全染色是指：（1）相邻的两个顶点染色不同；（2）相邻的两条边染色不同；（3）任意的点和与之关联的边染色不同,并用χvt(G)表示了图的点可区别全色数.如若上述（1）～（3）条件中只满足其中一个或两个条件时就被称之为图的一般全染色.本文仅考虑只满足（2）和（3）时的情形.

定义设G是一个简单图,k是正整数,f是V( G)∪E( G)到{1,2,3,…,k}的一个映射,对图G的一个全染色f,用C( u)表示点u和它所关联的边所染的颜色组成的集合,即C( u)={f( u)}∪{f( uv)|uv∈E( G)}.若对于V（G）中的任意两点u和v,都有C( u)≠C( v),则称f是图G的点可区别V-全染色,简称为图G的VDVT染色.

图G的一个VDVT染色所需要最少颜色的数目称为图G的点可区别V-全色数,记为(G).

引理对于简单图G,令ni是度为i（δ≤i≤Δ）的顶点的个数,若Kn存在μ-点可区别V-全染色,则有

在文献[4]中图mP2与mP3的点可区别E-全染色做了研究,其主要结论mP2与mP3图的点可区别V-全染色基本一致,本文中部分结果证明可参阅文献[4].

2 若干结论

定理1对于m条长为2的路的并的点可区别V-全染色,有

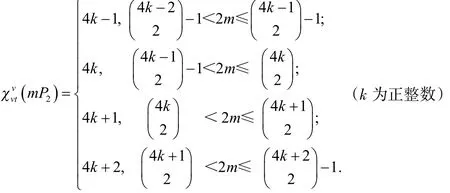
证明略.

定理2对于m条长为3的路的并的点可区别V-全染色,有

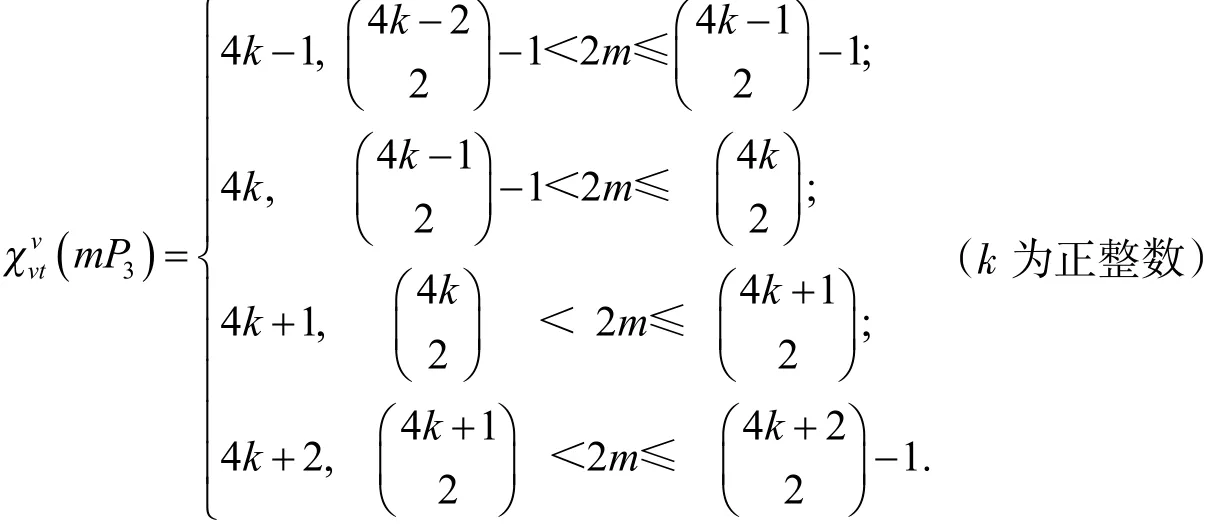
证明：当m=1,其染色方法以顶点色集合的形式表现为：{1,2},{2,1,3},{3,1},显然有(1P )=3；3

当m=2,其染色方法以顶点色集合的形式表现为：{1,2},{2,1,3},{3,1}；{3,2},{2,1,4},{4,1},显然有(2P )=4；3

当m=3,其染色方法以顶点色集合的形式表现为：{1,2},{2,1,3},{3,1}；{3,2},{2,1,4},{4,1}；{4,3},{3,2,4}, {4,2}；显然有(3P )=4；3

当m≥4时,染色方案参阅文献[4].

定理3对于m条长为4的路的并的点可区别V-全染色,有当m=1,2时,(mP)=4；4

当m=2时,在前面的基础上,给出其染色方法以顶点色集合的形式表现为：{1,3},{3,2,4},{4,3,1},{1,4}；{3,2},{2,4,1},{1,2,3},{3,4}；有(2P)=4；t4

当m=3,4,5时,在前面的基础上,第3,4,5条路的染色方法以顶点色集合的形式表现为：{5,1},{1,2,5}, {5,3,2},{2,5}；{5,3},{3,4,5},{5,2,4},{4,5}；{2,1},{1,3,5},{5,1,4},{4,2}；显然为VDVT全染色,且(mP)=5；4

当m≥6时,结论等价于

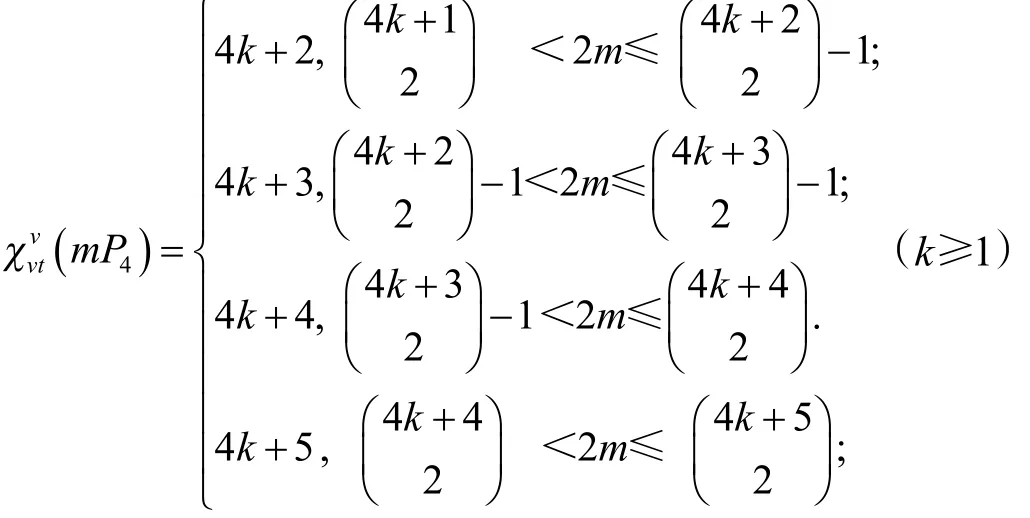
将本结论分4种情形讨论：

定理得证．

3 一个猜想

猜想对于m条长为n的路的并的点可区别V-全染色,其全色数若记为(mP),则：n

其中k为一个正整数．

4 结束语

本文依据简单图的点可区别V-全染色定义,给出了m条长为n的路的并的点可区别V-全色数,并给出了完整的证明过程,最后提出关于mPn的点可区别V-全染色猜想,为进一步探讨其他简单图的点可区别V-全染色提供了思想方法,丰富了图的点可区别全染色的结论,为进一步解决相关实际问题提供理论依据.

[1]Zhang Z F,Chen X E.On adjacent-vertex-distinguishing total coloring of graphs[J].Science in China（Ser A）,2005,48（3）：289-299．

[2]陈祥恩.n-方体的点可区别全色数的渐进性态[J].西北师范大学学报：自然科学版,2005,41（5）：1-3．

[3]张忠辅,陈祥恩,李敬文,等.关于图的邻点可区别全染色[J].中国科学A辑：数学,2004,34（5）：574-583．

[4]马宝林,刘娟,陈祥恩.图mP2与mP3的点可区别E-全染色[J].读写算,2010（9）：201-202.

[5]Ma B L,Chen X E,Liu J.2-distance coloring of strong product of graghs[J].山东大学学报,2010,45（3）：66-70.

[6]Zhang Z F,Qiu P X,Xu B G,et al．Vertex-distinguishing total colorings of graphs[J].Ars Combinatoria,2008（87）：33-45．

[7]马宝林.完全图的点可区别V-全染色[J].河南科技学院学报：自然科学版,2011,39（5）：44-46.

（责任编辑：卢奇）

Vertex distinguishing V-total chromatic number of mPn

Ma Baolin,Liu Juan,Wang Juntao,Ding Yurong
（Henan Institute of Science and Technology,Xinxiang 453003,China）

According to the definition and the method of the vertex-distinguishing V-total coloring,the vertexdistinguishing V-total coloring of the vertex-disjoint union of m paths with lengths n is discussed,and the conclusion and proof of the vertex-distinguishing V-total chromatic number are given,finally,proposed a conjecture,To further explore other simple graph vertex-distinguishing V-total coloring provides a theoretical evidence that enriched the graph vertex-distinguishing V-total coloring results．

simple graph；chromatic number；vertex-distinguishing V-total coloring；mPn

O157.5

A

1008-7516（2012）03-0065-04

10．3969/j．issn．1008-7516．2012．03．016

2012-03-08

马宝林（1978-）,男,回族,甘肃张家川人,硕士,讲师．主要从事图论及其应用研究．