通气空泡流中洞壁效应对空化数和压力场影响的研究

陈 鑫 ， 鲁传敬 ， 曹嘉怡 ， 李 杰 ， 郭建红

（上海交通大学a.工程力学系；b．海洋工程国家重点实验室；c.水动力学教育部重点实验室，上海 200240）

1 引 言

虽然高速水下航行体通常运动在广阔的水域中，但模型试验却是在有边壁或自由面的设备中进行的，邻近的固壁边界对于空泡形态和水动力可能产生显著的影响，即所谓洞壁效应。对闭式水洞，必须考虑阻塞问题。流动的限制促使局部流速增大，并形成比较大的空泡。在某个大于0的空化数下，流动可能被阻塞，从而无法得到更低的空化数。

关于空泡流洞壁效应的问题，以往的研究多集中在具有简单几何外形的自然空泡流问题上[1-2]，如平板、楔形体和圆锥等。Birkhoff等[3]以无升力楔形体的阻塞空泡流为研究对象，理论分析结果表明传统试验中定义的阻力系数对洞壁距离的影响十分敏感。Wu[4]采用不同的闭合模型，对闭式水洞中二维空泡流的外形和阻力系数进行了理论求解，并加以修正以适用相应的无界流动。

上述对洞壁效应问题的研究工作都是基于传统的势流理论，对空化流场内部流场的精细结构以及初生、发展、溃灭和脱落下泻等过程，这类方法缺乏有力的手段。另一方面，势流理论框架内无法考虑粘性，而粘性对空泡脱体点、空泡闭合区等有直接影响。

本文以一个带圆盘空化器的水下航行体模型为研究对象，基于均质平衡多相流理论和输运方程类空化模型，通过求解混合介质的RANS方程、RNG k-ε湍流输运方程和各相的质量输运方程，数值模拟了圆形截面水洞中的定常通气空泡流动，研究了闭式空泡水洞中洞壁效应对通气空泡流动中的空化数及流场压力分布的影响，并拟合得到了一定空化数范围内计算空泡尺寸和模型阻力系数的近似公式。

2 基本方程和数值方法

本文基于均质平衡多相流理论和输运方程类空化模型[5-7]，研究通气空泡流动。将由空气、水蒸汽和水组成的混合介质看成一种变密度单流体，各相共享同一压力、速度场，忽略相间滑移速度和重力效应。通过引入空气、水蒸汽和水的体积分量—αg、αv、αl，得到描述气、汽和液多相流动的控制方程。

连续性方程：

动量方程：

能量方程：

蒸汽相连续性方程：气相连续性方程：

考虑气体为可压缩理想气体，补充一个关联p、ρg和T的状态方程：

方程中混合介质的各相应满足相容性条件：

混合介质密度ρm和粘度μm由体积分量加权平均获得：

此外，采用两个独立的输运方程描述（4）式中汽、水间的质量传递过程：

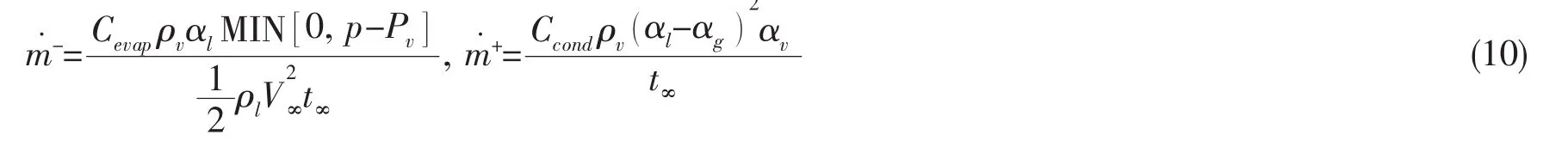
式中ui和xi分别指代速度分量和坐标方向；t为时间；p表示压力；μt表示湍流粘度；T为温度；kt是流体传热系数；cp为定压比热；ST为流体的内热源及由于粘性作用流体机械能转换为热能的部分；R0是气体常数；m˙-模拟的是水到水蒸汽的转换过程，这个量与液相体积分量以及当地压力和饱和蒸汽压Pv之间的差值成正比，该模型与Merkle等[8]使用的模型相同；对于水蒸汽到水相变过程中的质量传递率m˙+，采用了 Ginzburg-Landau 模型[9]；V∞为来流速度；Cevap、Ccond为经验常数，t∞是平均流时间尺度；下标 m、l、g和v分别指代混合介质、液相、气相和蒸汽相。

另外，采用标准壁面函数[10]的两方程RNG k-ε湍流模式[11]，使得上述粘性方程组封闭。

3 数值方法

本文应用有限体积法离散积分微分型控制方程。压力梯度项采用PEOSTO！格式[12]离散；动量方程的差分格式选用二阶逆风格式；湍流输运方程的差分格式选用一阶逆风格式；压力—速度耦合采用SIMPLE算法[12]。离散化后的代数方程系统的求解采用基于分离算法的Gauss-Seidel线性方程求解器，并结合“代数”多重网格法加速收敛。文中数学模型的建立及求解采用通用CFD软件—FLUENT实现。

水下航行体模型由圆盘空化器、双碗通气装置和轴对称后体组成，如图1（a）所示。总长L0=1 000mm，最大直径D=75mm，圆盘空化器直径Dn=0.2D。流动具有轴对称性，故简化为二维轴对称问题求解。图1（b）显示的是圆盘直径与水洞直径之比Dn:Dt为1:40情况下的计算域。取模型对称轴为x轴，坐标原点位于圆盘空化器顶面圆心处。入口距航行体圆盘0.513L0，出口距航行体末端L0，水洞壁距对称轴4D。网格划分采用多区块四边形网格，航行体头体部分结构较为复杂，图1（c）给出模型头部附近区块的网格划分情况；其余区块均属十分规则的四边形网格，不再一一图示。

边界条件设置如下：入口边界给定轴向速度10m/s、径向速度为0；出口边界压力给定24 867.8Pa；通气孔处为压力入口边界，给定总压、总温和静压；水洞壁和模型表面粗糙度为0，给定无滑移壁面边界条件。

图1 水下航行体模型、计算域及网格划分（Dn:Dt=1:40）：（a）模型对称面；（b）计算域与边界条件；（c）头体附近的网格Fig.1 The model,computational domain and grid(Dn:Dt=1:40):(a)The model section;(b)The computational domain and boundary conditions;(c)The grid near the head body

计算中，对于Dn:Dt分别为1:25、1:30、1:40、1:50和1:80的情况，模拟了不同空化数下的定常通气空泡流。

4 结果与讨论

由于通气量大小不同，通气空泡形态和压力分布情况也有所不同。小通气量下，通气空泡表现为局部空泡形态，空泡尾部存在明显的压力回复（图2（a））；而大通气量下，由于泡内压力增大通气空泡能够跨越模型锥段从而形成超空泡，且泡内压力大致相同，压力回复出现在模型后（图2（b））。

图2 典型通气空泡形态与压力等值线图（Dn:Dt=1:40）Fig.2 The shape of typical ventilated cavity and pressure contour(Dn:Dt=1:40)

图4中实线表示由计算得到的临界空化数的线性拟合曲线；而虚线为文献[1]中三维圆盘自然空泡流中阻塞空化数的势流近似解。当Dn:Dt较小时两者比较接近，而随着Dn:Dt的增大，两者的差别逐渐增大。差别产生的原因在于：一方面近似解没有考虑粘性的影响，边界层加强了流动的阻塞，另一方面由于通气及后体的影响，也使得本文阻塞空化数总是大于势流近似解。

图 3 σc与 M之间的关系Fig.3 The relationship between σcand M

试验中压力的测量通常是通过安置在水洞壁面上的压力传感器实现，本文采用数值模拟的方法分析了水洞壁面以及对称轴上的压力变化规律，有助于了解通气空泡流动情况下整个水洞中的压力场分布特点，为试验测量提供技术参考。

图5～7是圆盘与水洞的直径比Dn:Dt分别为 1:30、1:40 和 1:50 时，无物体流动（水洞内未放置模型）以及一组通气空泡流动（水洞内放置水下航行体模型）情况下，水洞主体段沿长度方向对称轴及壁面上的压力分布曲线，无物体流动算例中入口、出口和洞壁边界条件的设置与通气空泡流动算例相同。

图 4 σb与 Dn:Dt之间的关系，来自文献[1]Fig.4 The relationship between σband Dn:Dtfrom Ref.[1]

整体上看，除模型前后一定范围内，无论何种计算条件下，由于粘性带来的沿程损失，轴线和壁面上的压力沿流动方向基本呈下降的趋势。无物体流动情况下，水洞轴线和壁面上的压力按线性规律减小；通气空泡流动情况下，由于模型的置入和通入气体带来的能量变化，压力分布规律较为复杂。

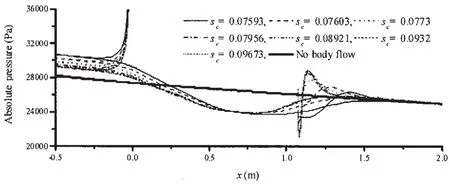
图5 当Dn:Dt=1:30时，水洞对称轴和壁面上的压力分布Fig.5 Pressure distributions on the axis and wall surface of tunnel at Dn:Dt=1:30

图6 当Dn:Dt=1:40时，水洞对称轴和壁面上的压力分布Fig.6 Pressure distributions on the axis and wall surface of tunnel at Dn:Dt=1:40

图7 当Dn:Dt=1:50时，水洞对称轴和壁面上的压力分布Fig.7 Pressure distributions on the axis and wall surface of tunnel at Dn:Dt=1:50

比较图5～7中水洞主体段起点到终点之间的压力差值，可以看出随着水洞直径的减小，各种流动情况下沿程的压力损失增大。由于计算中在出口边界给定常压，这使得水洞入口处压力升高。因此，按照空化数的定义，如将水洞入口测量的压力作为来流压力P∞，则水洞直径的减小将导致空化数增大。此外，由于水洞中的沿程压力损失还与水洞壁面的粗糙度（本文中计算取为0）有关。由于水洞壁面的粗糙会引起沿程损失的增大，与光滑壁面的水洞相比得到的空化数偏大，因此在水洞试验中应尽量保持水洞壁面光滑。

同一Dn:Dt下的通气空化流动中，圆盘空化器前由于流动滞止压力显著升高，而模型后端类似绕台阶流动，也出现明显的压力峰值。距圆盘约20Dn之前及距模型末端约40Dn之后的范围内，与水洞中未放置模型的流动相似，由于沿程损失水洞壁面和对称轴上的压力分布满足线性减小的变化规律。但是，在通气空化发生的区域内，由于流道变窄，流速增大，使得水洞壁面上的压力降低。其压力也不再满足线性规律，而是按照类似于二次曲线的规律变化。有鉴于此，在与本文计算条件相似的水洞模型试验中，应将来流压力的测压点置于距圆盘空化器至少约20Dn之前，可有效地减小模型本身对测量结果的影响。

同一水洞中，随着通气空化数的减小，水洞内压力升高的幅度逐渐增大。这是因为通气空化数的减小对应于通气量的增加和空泡的拉长变粗，意味着阻塞效应增强；同时通入气体的总动能增加，从能量转换的角度来看就表现为压力的升高。此外，由于空泡影响区域的扩大，水洞壁面上低压区域随着空化数的减小而增大。同时，模型后水洞轴线上的压力峰值则随着空化数的减小而减小。

根据计算结果发现不同圆盘水洞直径比下轴对称通气空泡的长度、最大直径以及模型阻力系数与空化数之间的关系曲线均具有相似性，表明它们与通气空化数以及圆盘水洞直径比这两个特征参数之间存在一定的函数关系。因此，本文利用数据处理工具Origin，通过非线性拟合和坐标平移等方法，给出了它们之间的近似关系式，适用于一定的通气空化数和圆盘水洞直径比范围。

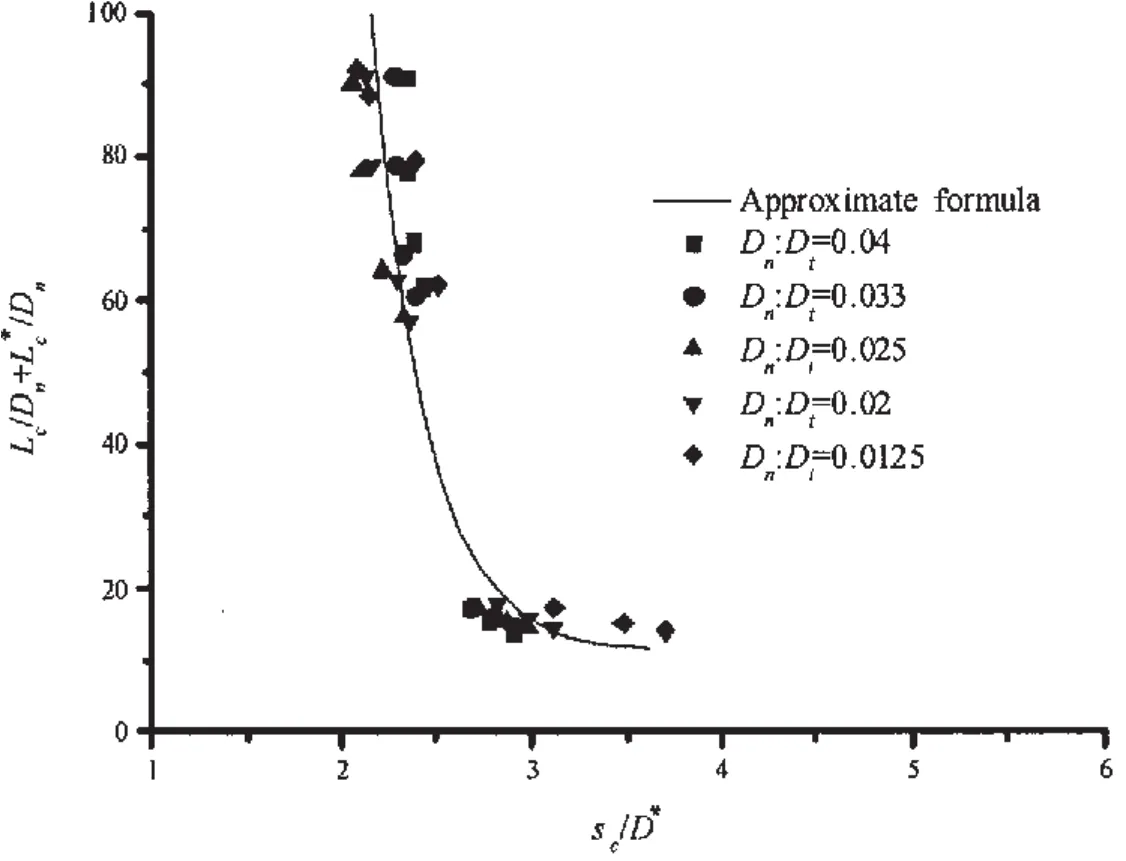
图8 通气空泡长度与空化数的归一化曲线Fig.8 Normalized correlation curve between ventilated cavity length and cavitation number

图9 通气空泡最大直径与空化数的归一化曲线Fig.9 Normalized correlation curve between maximum ventilated cavity diameter and cavitation number

图8～10为拟合后的归一化关系曲线（以实线表示）与计算数据（以离散的数据点表示）的对比结果。

图10 模型阻力系数与通气空化数的归一化曲线Fig.10 Normalized correlation curve between drag coefficient of model and ventialted cavitation number

5 结 论

本文基于均质平衡多相流理论和输运方程类空化模型，通过求解混合介质的RANS方程、RNG k-ε湍流输运方程和各相的质量输运方程，数值模拟了闭式水洞中带圆盘空化器航行体模型的定常通气空泡流动，分析了闭式水洞中洞壁效应对通气空化数、压力分布规律、空泡尺寸以及模型阻力系数的影响。在本文的计算条件下，可以得到以下结论：

（1）对于带圆盘空化器的水下航行体模型的通气空泡流动，计算得到的阻塞空化数线性正比于圆盘水洞直径比，且与三维圆盘自然空泡流的势流近似解基本一致，但由于粘性边界层、通气及后体的影响而略大于后者；

（2）在距航行体模型圆盘约20Dn之前以及距航行体模型末端约40Dn之后的区域内，由于沿程损失，水洞轴线和壁面上的压力分布满足线性规律；而在通气空化区域内，水洞壁面上的压力分布按照类似于二次曲线的规律变化；

（3）同一水洞中，随着通气空化数的减小，水洞内压力升高的幅度逐渐增大，水洞壁面上低压区域增大，而模型后水洞轴线上的压力峰值减小；

（4）根据计算数据，拟合得到了空泡长度、最大直径以及模型阻力系数的近似公式，适用的通气空化数与圆盘水洞直径比范围为：0.02＜σc＜0.12、0.01＜Dn:Dt＜0.04。

[1]Cohen H,Difrima R C.Wall effects in cavitating flows[C]//Second Symposium on Naval Hydrodynamics.Washington D.C.,U.S.,1958:367-390.

[2]Choi J K,Kinnas S A.Numerical water tunnel in two-and three-dimensions[J].Journal of Ship Research,1998,42:86-98.

[3]Birkhoff G,Plesset M,Simmons N.Wall effects in cavity flow II[J].Quart.Appl.Math,1952,9:413.

[4]Wu Y T,Whitney A K,Brennen C.Cavity-flow wall effects and correction rules[J].J Fluid Mech.,1971,49:223-256.

[5]Chen X,Lu C J,Wu L.An multiphase model on simulating a ventilated cavitating flow[J].Journal of Hydrodynamics,Ser.A,2005,20(Suppl.):916-920.(in Chinese)

[6]Zhang L X,Zhao W G,Shao X M.A pressure-based algorithm for cavitating flow computations[J].Journal of Hydrodynamics,Ser.B,2011,23(1):42-47.

[7]Chen Y,Lu C J.A homogenous-equilibrium-model based numerical code for cavitation flows and evaluation by computation cases[J].Journal of Hydrodynamics,Ser.B,2008,20:186-194.

[8]Merkle C L,Feng J,Buelow P E O.Computational modeling of the dynamics of sheet cavitation[C]//Third International Symposium on Cavitation.Grenoble,France,1998.

[9]Hohenberg P C,Halperin B I.Theory of dynamic critical phenomena[J].Rev.Mod.Phys.,1977,49(3):435-479.

[10]Launder B E,Spalding D B.The numerical computation of turbulent flows[J].Computer Methods in Applied Mechanics and Engineering,1974,3:269-289.

[11]Yakhot V,Orszag S A.Renormalization group analysis of turbulence I:basic theory[J].Journal of Scientific Computing,1986,1(1):1-51.

[12]Patankar S V.Numerical heat transfer and fluid flow[M].Hemisphere,Washington D.C.,1980.