两自由度运动圆柱绕流的离散涡方法模拟
董 婧,宗 智,李章锐,孙 雷,陈 伟
(1大连理工大学 工业装备结构分析国家重点实验室 船舶与海洋工程学院,辽宁 大连116024;
2中国舰船研究设计中心,武汉430050)
1 引 言
将钝体放置在具有一定速度的来流当中,流体会绕过结构物,在其后面形成尾流区,并在一定条件下从结构两侧交替地发生周期性泄涡现象。而旋涡的产生和脱落的作用,使物体受到横向和流向的脉动压力。对于弹性圆柱体或弹性支承的刚性圆柱体,所产生的脉动力会引起结构物的振动,反过来结构物的振动也会影响到流场,这种流固耦合现象称为涡激振动(Vortex Induced Vibration)[1]。当涡泄频率接近于结构的某一固有频率时,旋涡的泄放过程被结构的振动所控制,而使旋涡泄放和结构振动具有相同的频率,并在较大的流速范围内保持不变,这种现象称为“锁定”[2-3]。在发生锁定时物体的振幅显著增加,相位角发生突变。锁定现象会在旋涡脱落频率的很大范围内发生,锁定现象的机理尚不明确,大量的实验数据表明,通常当折合速度(Ur)在4.5到8之间时发生锁定现象。
海洋工程中的水下结构物经常采用圆柱体,其在波流作用下经常会发生涡激振动。当泄涡频率接近于结构的某一固有频率时,将会出现垂直于水流和圆柱体轴线方向的强烈振动,并且导致沿水流方向的振动和曳力增大。结构在两个方向上的强烈振动将引起震荡应力[4]。如果这种振动处于定常状态而连续发生,将会导致结构的疲劳破坏,降低其使用寿命。涡激振动是海洋立管遭受破坏的主要原因,另外,在水流冲刷及海底表面不平等环境因素作用下,铺设在海底的油气管道难免形成悬空段,直接暴露在水流作用下也会发生涡激振动。
关于结构涡激振动的研究,国外起于20世纪60年代,而我国则从80年代开始。研究范围涉及风工程和海洋工程;研究方法在早期侧重于试验研究,经过试验研究和理论分析并重的阶段,目前有重视理论分析的倾向[2-4]。众所周知,在通常的涡激振动中横向振动占主导地位,振幅大大超过流向振动,所以在研究过程中,很多学者采用简化的单自由度运动模型,只考虑横向振动而忽略了流向振动因素。那么这种做法是否科学合理?流向振动到底对涡激振动有何影响?本文的目的之一就要验证它。此外,本文还要对涡激振动的特征机理进行分析探讨。
本文采用离散涡方法(Discrete Vortex Method,DVM)来研究弹性支承的二维圆柱绕流的涡激振动(VIV)问题。对于圆柱的运动情况的研究分为单向自由度的横向运动和两向自由度的流向和横向共同运动两种情况。本文分别进行了单向自由度横向运动和两向自由度横向和流向共同运动这两种情况的模拟,并讨论了两者之间的联系,在一系列共16组(单向、两向运动情况各8组)数值计算中采用同Stappenbelt[6]的试验一致的各项参数,其中包括相同尺度的圆柱模型,均为单位长度,直径0.055 4m;从2.36到12.96变化的8个不同的质量比,以及随质量比的改变而改变的水中固有频率;从3到16变化的折合速度,以及随折合速度和固有频率的改变而改变的速度和雷诺数;还有不变的阻尼比,按试验值均为0.006。
本文首先对受力系数和响应位移进行了时域分析。从脉动升力和圆柱横向响应的振幅、周期和相位关系来判断锁定区域和非锁定区域,讨论在不同折合速度下,振动幅值的初始分支、上端分支和下端分支的变化规律,以及质量比的增加对振动幅值、锁定位置和锁定区域的影响。
接下来进行的是频域响应的分析,就泄涡频率和振动频率关系与Stappenbelt实验结果进行了对比,吻合完好,斯托哈尔数都处于稳定范围内,并且进一步讨论了质量比的增加对振动幅值、锁定位置和锁定区域的影响。
最后进行了不同折合速度、不同自由度下尾涡模式的分析,并结合一些文献中已发表的结果进行了对比和讨论。在分析的过程中认为数值模拟的绝大部分尾涡模式与实验和计算相一致,并且发现了新的尾涡模式。
2 离散涡方法的原理[1,5]
假设流体为不可压缩流体,那么它的控制方程为N-S方程:

因涡量ω=▽×V,对上式取旋度,得:

如只研究二维平面流,则ω·▽V=0,由此得:

离散涡方法是将连续的涡量场离散,在拉格朗日框架下进行求解,着眼于追踪每个涡元粒子运动的时间历程。对于不可压缩的粘性流动,上世纪90年代Chorin[7]提出了算子分裂法,涡量方程(2)可分裂成对流和扩散两部分分别进行求解。
对流部分:

粘性扩散部分:

其中,υ为流体的运动粘性系数,ω为涡量,ψ为流函数。
方程(4)代表二维不可压缩无粘性流动,如果当无穷远处的自由流动条件已知,流场中不存在外部边界时,它的解就是著名的Biot-Savart定律:

式中 r、r′,表示矢径,V∞代表无穷远处的速度。
而扩散部分与粒子的布朗运动的解具有相同的形式,在无粘解的基础上,可以采用随机走位的方法来模拟,下面具体介绍随机走位的方法。
方程(5)为一维热扩散型方程,它的基本解是格林函数:

这与一个均方差为零、标准差为σx的随机变量的概率密度函数在形式上是一致的,即:


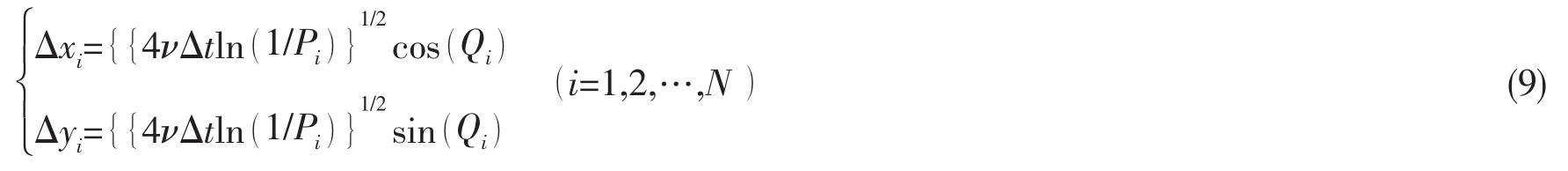
其中N是流场中涡元总数,下标i为涡元编号,Pi和Qi分别是在(0,1)和(0,2π)区间内均匀分布的两个相互独立的随机数。
假设t时刻涡元的位置xi(t),yi(t)已给定,则t+Δt时刻涡元的随机走位为

在此应当指出的是,每个涡元的环量Γi是不随时间变化的。
3 离散涡方法的数值实现
离散涡方法的实质是用离散的点涡来模拟物体的边界层和剪切层,认为粘性影响集中在物体附近很薄的边界层以及分离后的剪切层内,其涡量来自于不断分离出来的点涡供给,在整个流场中涡量守恒。离散涡方法主要分为物面涡的生成、涡元的对流和扩散、涡元的消除和融合,物体受力计算等几个方面。
首先,将连续的涡量离散成为若干个涡元(如图1所示),根据流场条件计算出每个涡元的位置和强度。
其次,要求出流场中的速度分布,每个涡元的速度都由两部分叠加而成,一部分为定常流场的绕流速度;另一部分为涡元之间的诱导速度,可以通过泊松方程▽2ψ=-ω和边界条件联立求解。
在求解边界条件时,本文采用流函数列式的方法即涡元法(Vortex Element Method)[1,5]。 涡元法利用物面是一条流线
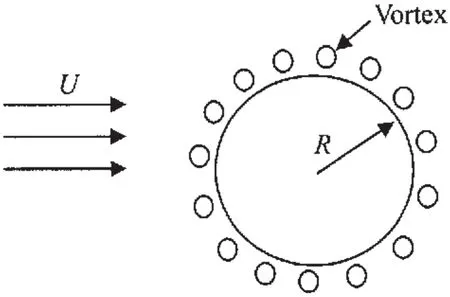
图1 离散涡元示意图Fig.1 Position of vortex generation
来满足物面条件,通过离散的流函数列式,可以确定各新生涡元的强度。Spalart等人在1983年引入了刚性涡,其半径为σ,周向的诱导速度为:

当涡元的诱导速度为(5)式时,其相应的流函数为

则在控制点k处的流函数为:
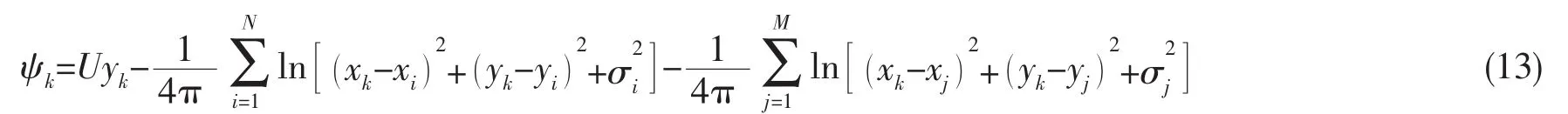
其中N和M分别为新生涡元总数和尾涡涡元总数。
当圆柱静止不动时物面为一条流线,则

将(13)式代入(14)式可以得到一组以环量Γ为变量的线性方程组:

其中系数矩阵AI仅与控制点和新生涡元的位置有关,列向量b由来流和尾流中的涡元分布来决定。
关于物体的受力,Quartepelle和Napolitanp在1983年推导了用整个流场的信息来表示的受力系数公式[9]:

对于运动的圆柱,(14)式应改写为:

其中VB圆柱运动的速度矢量,n为控制点k处的物面法向。相应的(15)式中的列向量b中也会增加与速度有关的因素,而系数矩阵AI保持不变。此时(16)式必须加入圆柱的惯性力项,于是改写为:


无论圆柱运动与否,现有涡元的速度都由环量Γ表示如下:从上式中可以看出,在求取每个涡元的速度时,都需要计算其他所有涡元对它的诱导速度,如果把计算单个涡元速度的运算次数计为NV,那么在一个时间步内计算所有涡元的速度,则需要N2V次。而每一时间步内都有固定数目的新生涡元进入尾流中,随着时间的增长NV直线增加,其结果必然导致单个时间步长的计算时间越来越长,计算缓慢。因此,必须有效控制尾流中涡元的数目。同时,在涡的对流和扩散中,涡元会越过边界移动到圆柱内部引起混乱,也必须予以消除。Spalart提出的涡融合机制认为,如果两涡元满足下面(20)式的条件就进行合并。

其中z=x+yi为涡元在复平面内的位置,D0和V0都是控制参数,其中D0∝U∞,控制圆柱附近的涡元数目;V0∝10-6U∞,控制流场中涡元总数。合并后新涡元的位置为(21)式,强度为(22)式。

运动圆柱的涡激振动问题可以从两方面入手,即强迫振动和自激振动。本文进行了自激振动的模拟,分别采用单向自由度和两向自由度的弹簧-阻尼质量系统来模拟二维圆柱,如图2所示。
圆柱在横向和流向的运动方程可分别表示为:
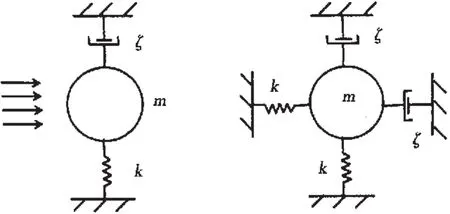
图2 弹性支承的圆柱模型Fig.2 Vibration model of elastic mounted cylinder

其中m为圆柱的质量,c为系统阻尼系数,k为弹簧刚度系数。Fx(t),Fy(t)分别为流向和横向的流体力,它们可以分别用阻力系数和升力系数表示为:

将(23)、(24)式转化成无量纲形式为:
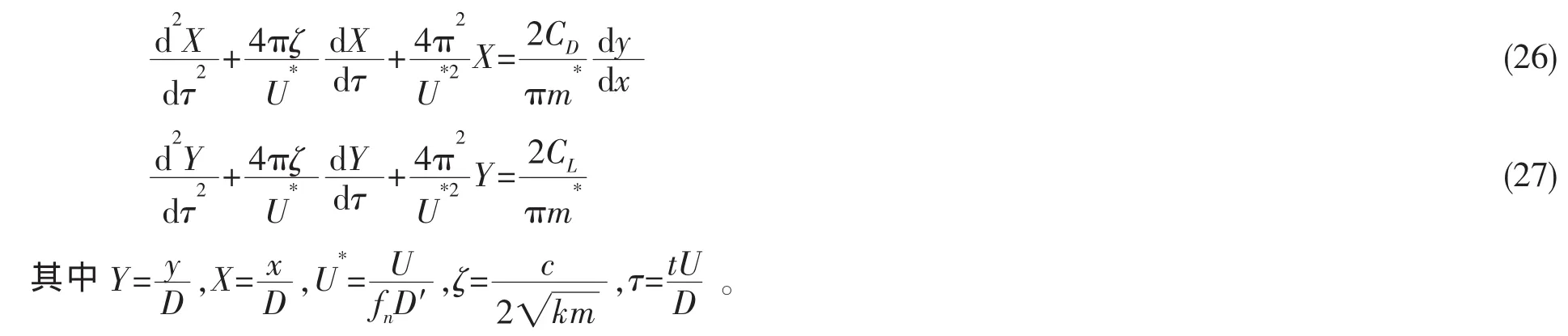
采用4阶精度的Runge-Kutta法进行迭代求解。
4 数值结果和实验对比
在两向自由度横向振动的数值模拟中,为方便与其它试验和数值结果对比,本文选用Stappenbelt[3]的实验参数,如表1所示
除表1所列的参数之外还有其他一些在这8组实验当中不变的参数,包括圆柱直径D为0.055 4m,折合速度Ur从3变化到16,以0.5递增,时间步长Δt=0.1D/U,每时间步有新生涡120个,总共1 200步。雷诺数Re随折合速度Ur变化,其值在2.84×105到1.52×106之间,每组实验都分为单自由度横向振动和两自由度流向和横向耦合振动两种情况计算,为方便表述,分别记为1dof和2dof。
在图 3(a)到(f)给出了质量比为 2.36时的 6个典型时刻的升力系数CL、阻力系数CD、无因次化的横向位移Y/D、流向位移X/D的时程曲线。通观这6幅图可以得到以下结论:
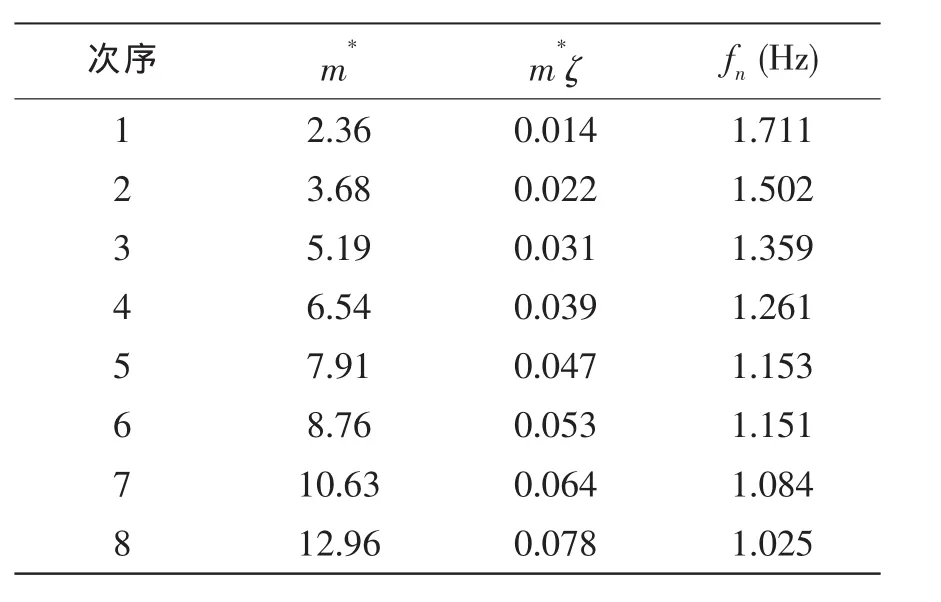
表1 振动模型计算参数Tab.1 Parameter of vibration model
从受力系数来看,阻力系数CD始终处于一个较高的水平,其波动的幅值较小,这其中稳定的部分是由均匀来流的持续冲击所致,而波动的部分是由泄涡产生的脉动压力所致,所以从上面的几幅图的比较可以看出,折合速度越大,阻力系数的平均值就越高,这是符合常理的。升力系数CL的平衡位置在0附近,而波动的幅值相对较大,这是由于升力系数只与泄涡产生的脉动压力有关,横向的脉动压力幅值大于流向的脉动压力幅值,而均匀来流的持续冲击力对升力系数没有直接的影响。升力系数CL的脉动周期始终约为阻力系数CD脉动周期的2倍,这也是由泄涡产生的脉动压力所致。从位移曲线来看,流向位移X/D受阻力系数CD影响,在一个较高的水平上波动,在第一个周期里有较高的幅值,这是由于在静止状态突然加力所致,在后面的几个周期里就会平稳下来,不过这也在另一个侧面说明了本文计算程序的稳定性。横向位移Y/D受升力系数CL影响,则在0轴上下波动。
图3(a)中曲线对应折合速度Ur=4.5,处于初始分支。此时升力系数CL和阻力系数CD出现阶段性的脉动,周期大概在25左右,这与弹簧—阻尼系统在两个方向的固有频率接近有关。横向位移Y/D与升力系数CL的周期和相位都是一致的,这一现象在初始分支中普遍存在,并与众多试验和数值模拟结论相一致[10-12]。图3(b)中曲线对应折合速度Ur=6,处于初始分支和上端分支的临界状态,横向位移Y/D的振动幅值较大且振动平稳,但相位和周期仍然符合初始分支的特点。图3(c)中曲线对应折合速度Ur=7.5,处于上端分支,横向位移Y/D的振动幅值较大且振动平稳,横向位移Y/D与升力系数CL的周期一致而相位角相差180°,这是上端分支锁定区域的典型特点。图3(d)中曲线对应折合速度Ur=9,处于上端分支和下端分支的临界状态,此时横向位移Y/D与升力系数CL仍然是周期一致而相位角相差180°,而横向位移Y/D的振动幅值开始下降且振动不稳定。图3(e)、(f)处于下端分支的中段和末段,在这一阶段,横向振动逐渐减退,流向振动和横向振动的幅值相当。

图3 升力系数CL、阻力系数CD和流向位移X/D、横向位移Y/D的时程曲线,其中质量比m*=2.36,水中固有频率Fn=1.711Fig.3 History of lift coefficient CL,drag coefficient CD,stream-wise displacement X/D,and transverse displacement Y/D,here mass-ratio m*=2.36,natural frequency in water Fn=1.711
图4到图7为不同质量比时单自由度1dof和两自由度2dof的横向运动无因次振幅A/D同实验值的对比,横坐标为折合速度Ur。为与实验的描述一致,这里用T表示横向运动,T&S表示横向和流向耦合运动。从图中可以看出,本文计算结果与Stappenbelt实验值的总体趋势向一致,会出现明显的初始分支、上端分支和下端分支。在两自由度的振动中质量比较低时还会出现超上端分支,而后振幅骤降。从相同质量比时1dof和2dof振动情况的比较来看,相同折合速度下2dof振动时的幅值更大,这一特征随着质量比的减小而增加,这说明了流向振动的参与对横向振动会有促进作用。而从不同质量比之间的对比可以看出,随着质量比的增加,无论是1dof还是2dof振动,其幅值都会随之下降。本文计算结果的不足之处在于模拟到的下端分支处的振幅偏高。
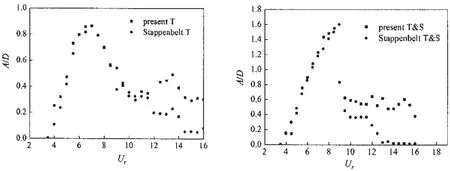
图4 m*=2.36时单双自由度横向无因次振幅A/D同实验对比Fig.4 Non-dimensional transverse amplitudes A/D of 1dof and 2dof compared with experimental results for m*=2.36
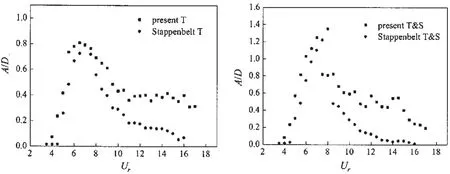
图5 m*=3.68时单双自由度横向无因次振幅A/D同实验对比Fig.5 Non-dimensional transverse amplitudes A/D of 1dof and 2dof compared with experimental results for m*=3.68

图6 m*=5.19时单双自由度横向无因次振幅A/D同实验对比Fig.6 Non-dimensional transverse amplitudes A/D of 1dof and 2dof compared with experimental results for m*=5.19
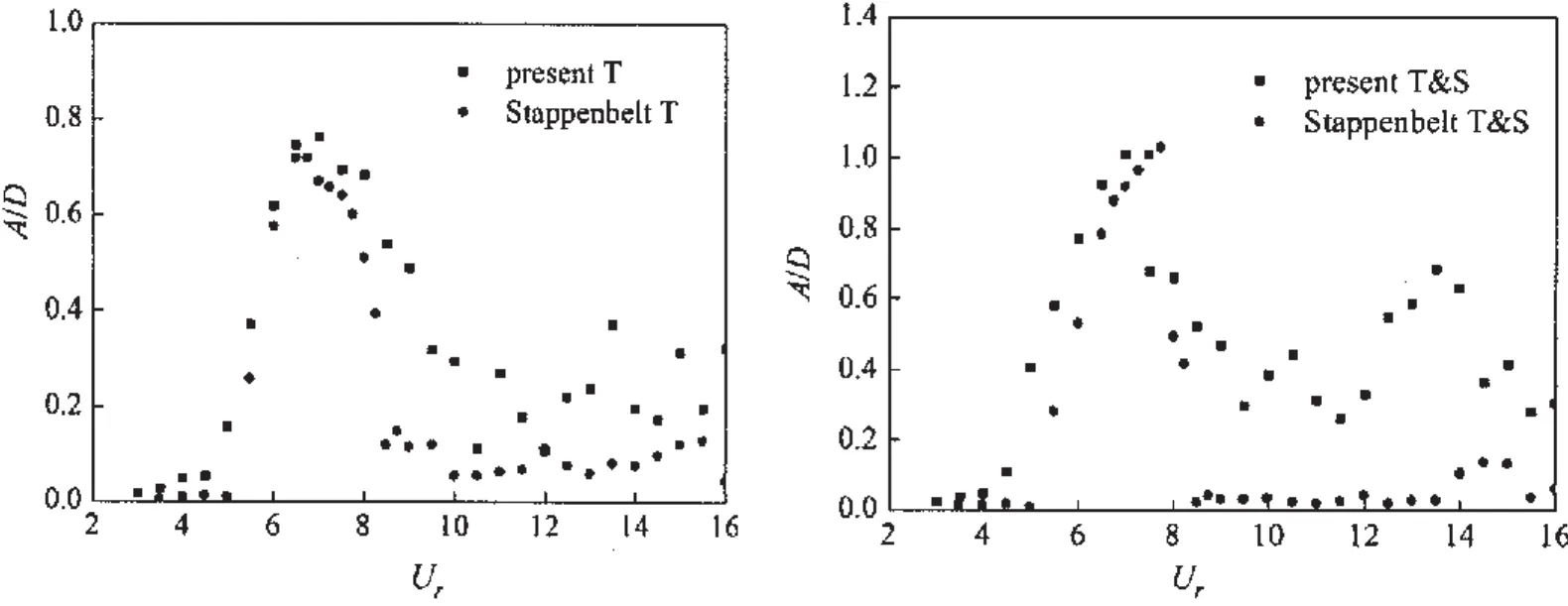
图7 m*=6.54时单双自由度横向无因次振幅A/D同实验对比Fig.7 Non-dimensional transverse amplitudes A/D of 1dof and 2dof compared with experimental results for m*=6.54
图8共有10组质量比的单自由度运动时无因次振动频率和泄涡频率图,横坐标为折合速度。其中前两幅图为Stappenbelt实验中已发表的数据。后8幅图为本文计算结果,与实验结果的趋势一致,在锁定区域以内,泄涡频率fs和圆柱振动频率fv一起锁定在固有频率fn附近;在锁定区域以外,泄涡频率fs沿折合速度会形成一条直线,在这条直线上有一个相对稳定的斯托哈尔数St,这将在表2中说明。
表2为单自由度振动模型的锁定参数 (包括初始锁定的折合速度Ur和锁定区域折合速度的范围ΔUr)及斯托哈尔数St的计算结果同Stappenbelt实验值的对比。从折合速度Ur的比较中可以看出,两组数据的大小相接近,且都随着质量比的增加而增加。从锁定区域的范围ΔUr可以看出,本文计算与实验结果符合得较好,最多相差0.6,且都随着质量比的增加而减小。从斯托哈尔数St的比较可以看出,本文计算与实验结果符合得较好,最多相差0.08,且都随着质量比的增加而增大。双自由度振动模型的计算结果与之类似。
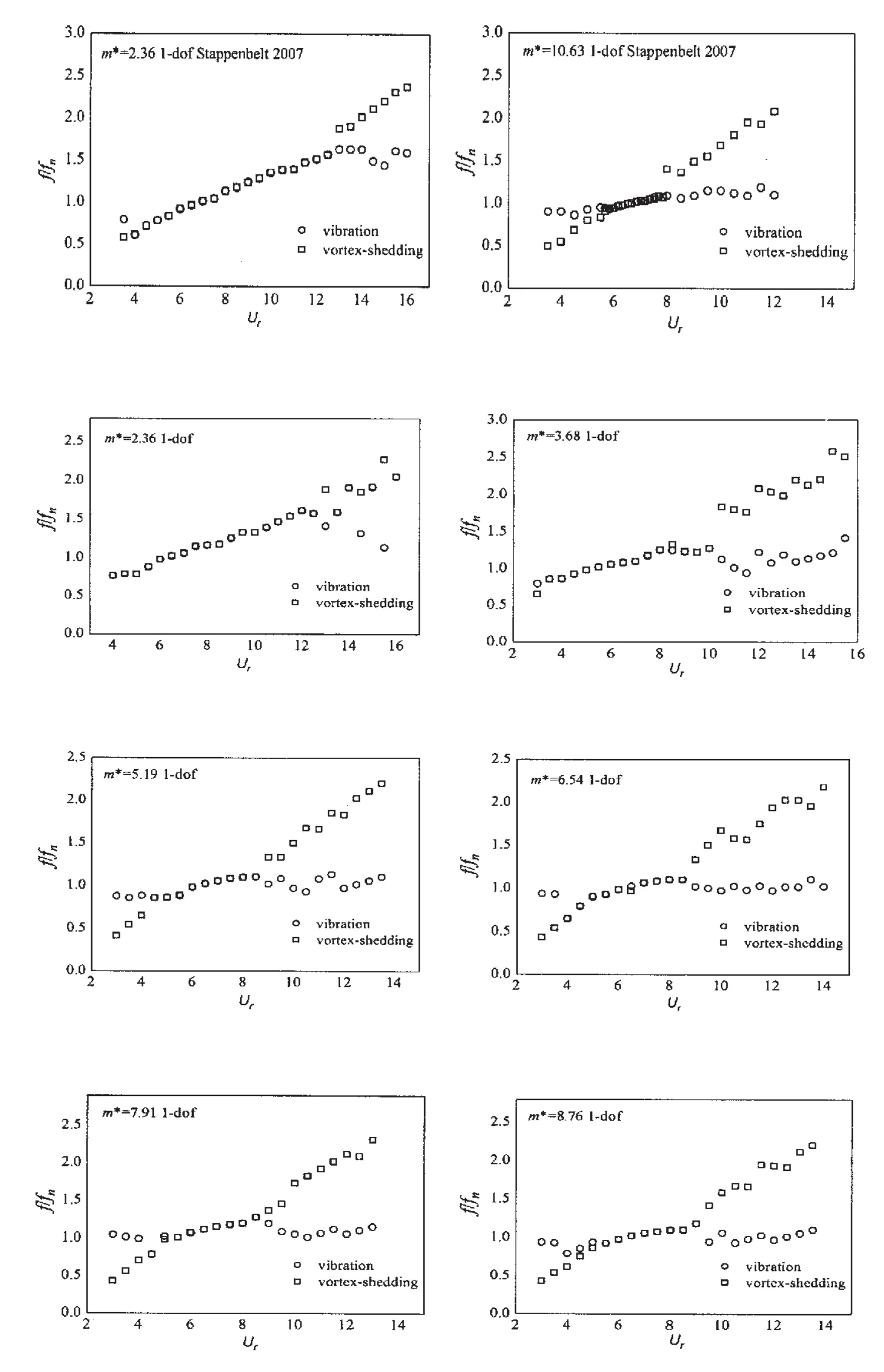

图8 无因次振动频率和泄涡频率关系图Fig.8 Non-dimensional vibration and vortex shedding frequencies
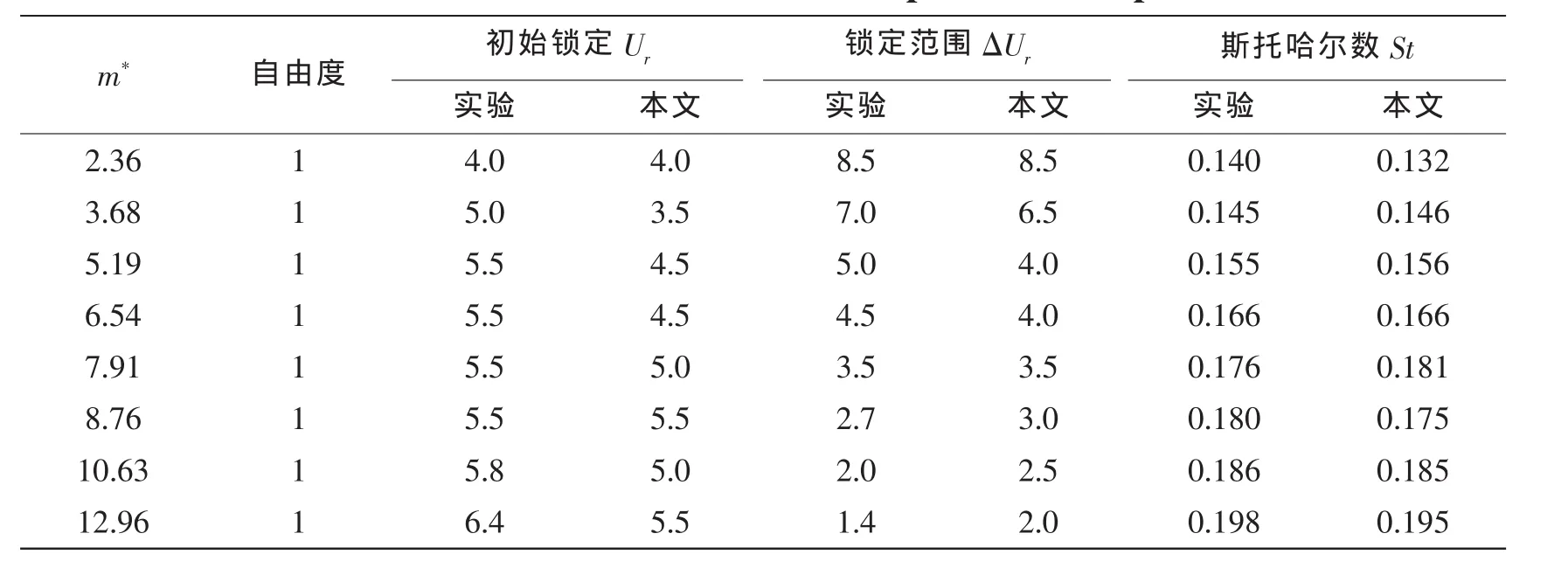
表2 锁定及斯托哈尔数计算结果同实验对比Tab.2 Lock-in values and Strouhal number compared with experimental results
横向振动响应分支在振幅上有较大变化,相应的尾涡模式也有明显的差异。在本文的计算结果当中,Re在105以上,无论是1dof还是2dof的振动,在初始分支中都表现出2S模式(two single vortex shedding per cycle)如图9所示,而通常情况下在上端分支和下端分支所对应的尾涡则为2P模式(Two pairs vortex shedding per cycle)。上端分支所对应的尾涡中2P模式为一强一弱的两个旋涡如图10所示,其中小的旋涡会在尾流中不断的对流和扩散中消失,在流场中较远处只剩下较大的旋涡;而下端分支所对应的尾涡中2P模式为强度相当的两个旋涡,如图11所示,这两个漩涡在流场较大范围内运动都不会消失。这与黄志勇[11]文献中描述的结果类似。而本文的计算中还发现了,在个别上端分支中在一个周期内先是产生两条细长的涡带而后分化成4个小的旋涡,暂时把这种尾涡模式也归为2P模式的一种,如图12所示,本文认为这是从2P模式到2T模式的一种过渡模式,其生成机理有待于进一步研究。

图9 初始分支的2S泻涡模式Fig.9 2S model of vortex shedding in the initial branch
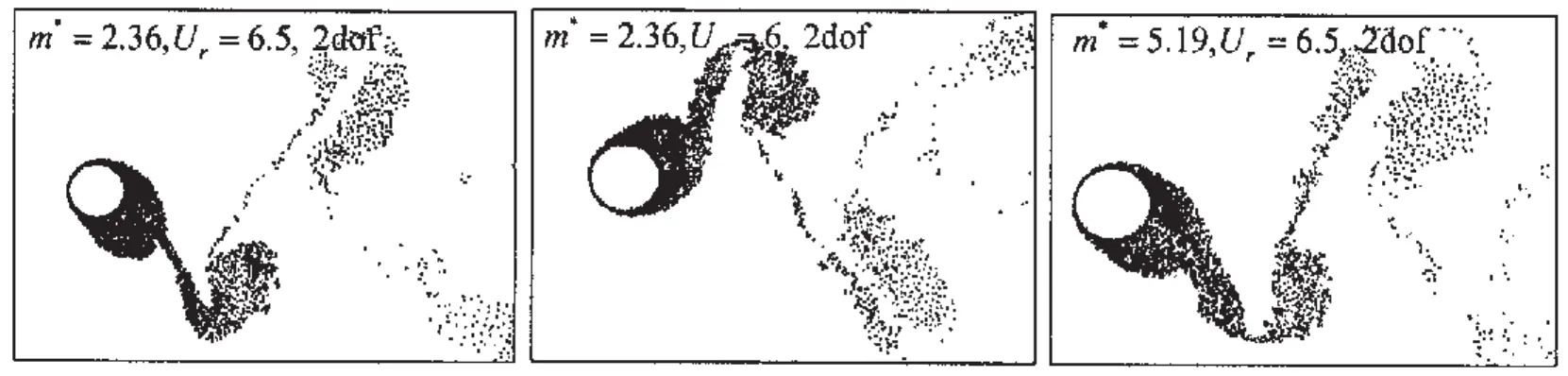
图10 上端分支中两旋涡不等的2P泻涡模式Fig.10 2P model of vortex shedding in the upper branch(each pair of vortex blobs with unequal scales)

图11 下端分支中两旋涡相等的2P泻涡模式Fig.11 2P model of vortex shedding in the lower branch(each pair of vortex blobs with equal scales)
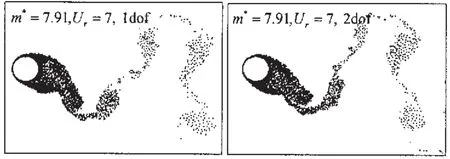
图12 特殊的2P泻涡模式Fig.12 The special 2P model of vortex shedding

图13 超上端分支中的2T泻涡模式Fig.13 2T model of vortex shedding in the super upper branch
2T模式(Two triplets of vortices per cycle)在一个泄涡周期内产生两组涡团,每个涡团产生三个旋涡,其中两个旋涡的旋向与另一个相反。出现在两自由度振动的上端分支的顶点处,也就是所说的超上端分支,如图13所示。
在一些过渡阶段还会出现以上多种尾涡模态交替出现的情况,是由于运动圆柱的位移和速度的变化所致,在这里不做详细介绍。
5 结 论
本文利用离散涡方法对二维弹性支承圆柱绕流涡激振动问题进行了较为详细的计算,可以得到以下结论:
首先对受力系数和响应位移进行了时域分析。从脉动升力和圆柱横向响应的周期和相位关系可以看出有明显的锁定区域和非锁定区域,观察到在不同折合速度下,振动幅值有着明显的初始分支、上端分支和下端分支的变化,并且随着质量比的增加,振动幅值会有所下降,这与众多观察和实验的本质特征一致。
在单自由度和两自由度振动幅值的对比中发现,两自由度振动在上端分支处的幅值明显高于单自由度的情况,说明流向振动对横向振动有促进作用,用单自由度建立的涡激振动模型预报结果将会偏于保守,在此建议在建立涡激振动模型时,流向振动因素应当予以重视。
从进一步的频域分析结果来看,泄涡频率和振动频率关系与Stappenbelt实验结果吻合完好,斯托哈尔数都处于稳定范围内,并且验证了随着质量比的增加,初始锁定时的折合速度会提高,而锁定区域的范围会减小。
在进行尾涡模式分析时与黄志勇在文献中已发表的结论基本一致,并且在上端分支中发现了新的尾涡模式—有4个小的旋涡的2P模式。本文认为这是从2P模式到2T模式的一种过渡模式。
[1]Lewis R I.Vortex element method for fluid dynamic analysis of engineering systems[M].Cambridge:Cambridge University Press,1991.
[2]Gabbai R D,Benaroya H.An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J].Journal of Sound and Vibration,2005,282(3):575-616.
[3]Liao Jungchi.Vortex-induced vibration of slender structures in unsteady flow[M].Cambridge,USA:Massachusetts Institute of Technology,2002.
[4]Pan Zhiyuan,Cui Weicheng,Liu Yingzhong.A predicting model for self-excited VIV of a circular cylinder at low massdamping[J].Journal of Ship Mechanics,2005,10(5):115-124.(in Chinese)
[5]Saltara F.Meneghini J R,Fregonesi R A.Numerical simulation of flow around elastically mounted cylinder[J].International Journal of Offshore and Polar Engineering,2003,13(2):99-104.
[6]Stappenbelt B,Lalji F.Low mass ratio vortex-induced motion[C].16th Australasian Fluid Mechanics Conference,2007,12:1491-1497.
[7]Chorin A J.Numerical study of slightly viscous flow[J].Journal of Fluid Mechanics,1973,57:785-796.
[8]Lewis R I.Vortex element method for fluid dynamic analysis of engineering systems[M].Cambridge:Cambridge University Press,1991.
[9]Chorin A J.Numerical study of slightly viscous flow[J].Journal of Fluid Mechanics,1973,57:785-796.
[10]Huang Zhiyong,Pan Zhiyuan,Cui Weicheng.Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio[J].Journal of Ship Mechanics,2007,11(1):1-9.(in Chinese)
[11]Khalak A,Williamson C H K.Dynamics of a hydroelastic cylinder with very low mass and damping[J].Journal of Fluids and Structures,1999,13:813-851.
[12]Zhou C Y,So R M C,Lam K.Vortex-induced vibrations of an elastic circular cylinder[J].Journal of Fluids and Structures,1999,13:165-189.

