基于高斯脉冲的超短波电台波形设计研究＊

王广辉 郑巧珍

（武汉船舶通信研究所 武汉 430079）

1 引言

1979年由日本国际电报电话公司提出的GMSK调制方式，由于其较高的频带利用率和功率效率，特别是带外辐射小，很适合工作在VHF和UHF频段［1～2］。同时数字化战场和数字化部队的建设要求战术无线电台不仅支持传统的语音传输，还要支持不断增长的数据业务，因此高速数传电台的研究和发展是必要和急需的［2］。而海军现役超短波电台内嵌波形支持明密话以及数传功能，基带波形目前支持2400bps与4800bps两种速率（不具备自适应能力），以该波形来支持分组网协议，存在着带宽与可靠性或适应信道能力不足等问题。课题要求在原有对海超短波电台中VHF通信子网的物理层使用25KHz的调频波道作为传输通道，实现19.2KHz的数传业务，以支撑链路层和网络层等上层网络所要求的传输性能。

在这种工程实践背景要求下，本文通过计算机仿真，分析了高斯波形在不同检测方式和BT值下的性能指标以及不同定时偏差和抽样点数对系统性能的影响程度。

2 高斯基带波形设计

GMSK调制是把输入数据经过Gauss低通滤波器进行预调制滤波后，再进行 MSK调制的数字调制方式［3］，如图1所示。它在保持恒包络的同时，能够改变Gauss滤波器的3dB带宽对已调信号的频谱进行控制。

图1 GMSK调制基本框图

其数学表达式可写为

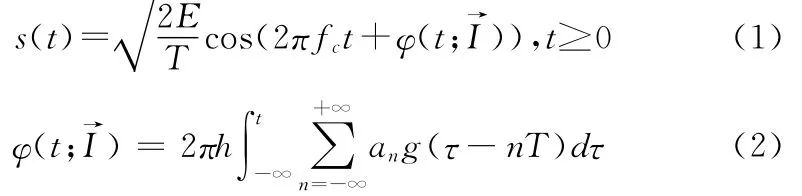
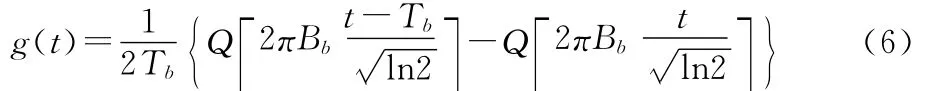
基带Gauss脉冲成形技术平滑了MSK信号的相位曲线，因此稳定了信号的频率变化，更进一步地限制了信号带宽。和矩形脉冲的相位路径对比，如图3所示。

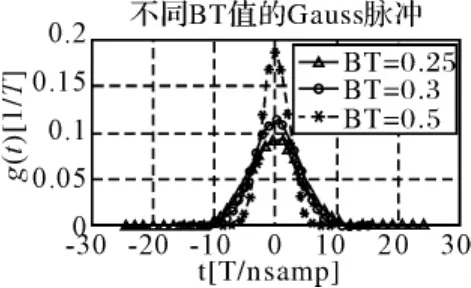
图2 不同BT值的Gauss波形

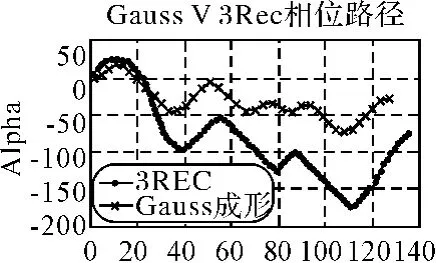
图3 Gauss脉冲和矩形脉冲相位路径对比

预调制Gauss滤波器将全响应信号转换为部分响应信号，每一发射符号占据几个比特周期即引入了符号干扰（ISI），因此实际上GMSK是牺牲了误码性能，以此换取了较好的带宽利用率和恒包络特性。但对接收端的符号检测带来了相应的困难，全响应的逐符号检测方法已很难达到最佳的检测性能［1，4］。

3 存在ISI的MLSE最佳检测-Viterbi算法

根据ungerboeck的观测模型［5～6］，收端对收到的信号进行匹配滤波后提供符号检测信息的充分统计量，因此可以直接对基带波形进行处理。由于基带波形符号间是相互关联的，基带信号具有的内在记忆特性使得最佳检测器应根据接收信号的一段观测序列做出最小错误概率判决。

接收信号为

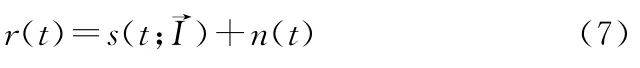
在最佳采样点下归一化系数：

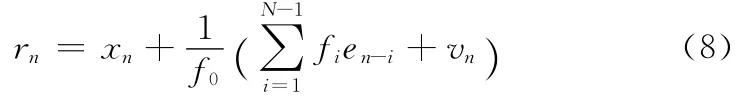
作似然函数：

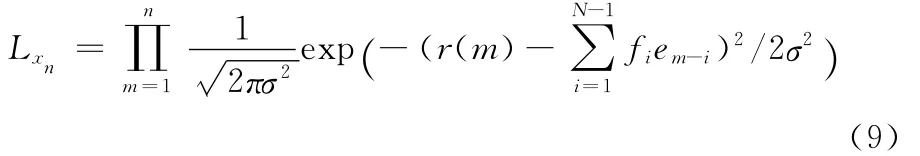
取对数运算：

设I＾为接收机所收到的估计序列。MLSE准则的思想就是通过状态网格搜索最小欧氏距离的路径，找到一个最为可能的估计序列，使得条件概率P（I→｜r（t））最大，即在接收到的信号为r（t）条件下，序列I→具有最大的出现概率［7］。

维特比算法是一种顺序网格搜索算法，用来执行MLSE准则。该算法的检测过程可以概括为“加－比－选”操作［8～9］。其两状态网格图如图4所示。

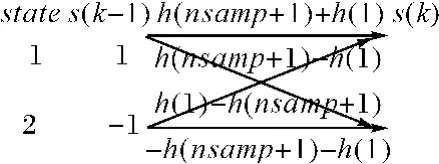
图4 ISI状态网格图

Ungerboeck观测模型中当前符号除了受到前一符号的影响外，未来的符号也对其产生干扰，本文采用A.Hafeez和R.Schober提出的预先判决反馈算法来处理未来符号的影响［10］。在计算当前状态的分支度量时，对下一符号做出最大似然意义上的的预判决，得到更为精确的欧式距离表达式。

判决反馈序列检测算法对于存在符号间串扰的序列检测和多用户检测中得到广泛地研究和应用［11］。采用对未来符号的判决反馈机制，即在最小错误概率意义上解决了未来符号对当前符号最大似然检测时的影响，也考虑到运算量的复杂度，达到了系统所要求的传输性能。

4 仿真结果分析

图5给出了Gauss波形在高斯白噪声信道（AWGN）下的仿真结果。由图可以看出，BT值对基带波形性能有很大影响。在BER＝10－5下，当BT＝0.5时，归一化信噪比Eb／N0达到10.5dB；当BT＝0.3时，归一化信噪比为12.7dB。采用不同的符号检测方法对系统误码率也有不同的影响。当BT＝0.3时，采用Viterbi检测比逐符号检测有0.7dB增益；当BT＝0.25时，逐符号检测已经达不到系统所要求的BER。当BT＝0.5时，获得的增益极少，因为当BT＝0.5时符号间的干扰程度很低，相关性较弱。由此可以得出结论，Viterbi检测所能得到的增益不仅与干扰的深度有关，还与干扰的程度有很大关系。

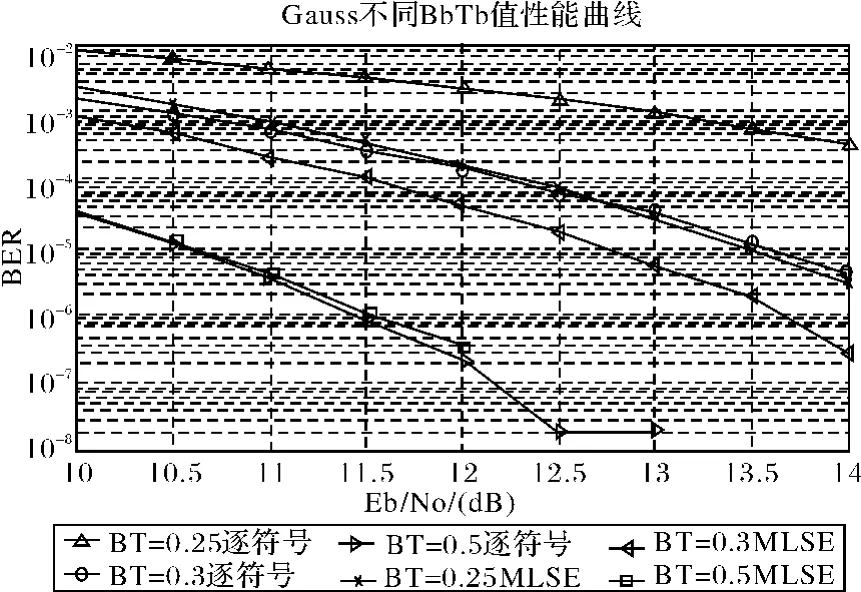
图5 不同BT值和符号检测方法下波形性能

上述仿真在理想采样的前提下得出的曲线，实际系统中由于信号传输时延τ的随机性和收发双方参考时钟的不稳定性或漂移，精确的抽样时刻tn＝nT＋τ往往是难以获得的，定时偏差对系统性能的影响也是项目指标设计时要考虑的重要方面。图6给出了不同定时偏差下的仿真结果。由图可以看出，在BER＝10－5下，定时偏差1／8个符号周期相比最佳抽样点有2dB左右的信噪比损失，偏差1／16个符号周期时有1dB的信噪比损失。

基带波形采用不同抽样点数既影响系统的波形性能，又影响接收端的计算量。图7给出了不同抽样点数对系统性能的影响程度。由曲线知当nsamp＝4、8、16时，在BER＝10－4下，归一化信噪比分别达到9.3、12.3和15dB左右。故采用多大的抽样点数对系统性能影响较大，同时计算量也会随着抽样点数的增加而增加，实际工程实现时应结合硬件体系综合考虑。

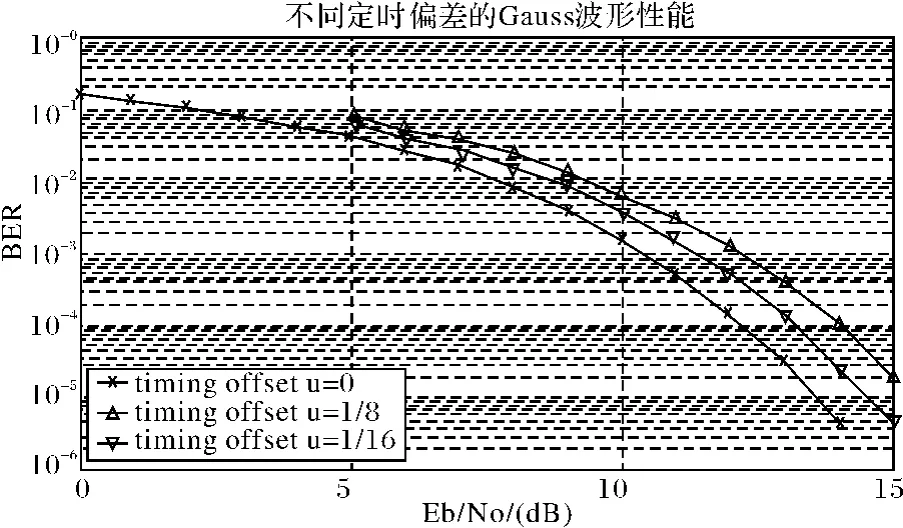
图6 不同定时偏差下波形性能

图7 不同抽样点数下的波形性能

5 结语

本文以实际工程项目为背景，仿真了超短波电台中拟采用高斯波形所能达到的系统性能，得出了一些有意义的曲线和结论，为工程方案设计、器件选型和硬件设计等提供了理论依据和有力的指导。

进一步的研究方向是：在引入差错控制编码的情况下，系统性能的提高情况。MLSE的Viterbi解调是硬输出的比特流，使得信道译码时无法采用软判决的译码方法，限制了系统性能的进一步提高。将Turbo码的迭代译码思想运用到串行级联系统中，争取更多地提高功率效率和系统性能。

［1］John G.Proakis.Digital Communications［M］.5thed.New York：McGraw-Hill，Publishing House of Electronics Industry，2009：160-182.

［2］沙楠，高宇.VHF高速数传电台调制方案设计与实现［A］.中国科技文献.CHINA SCI-TEC.2008：1464-1467.

［3］李斌.基于CPM的窄带高效数据传输系统［D］.西安：西安电子科技大学，2010：5-13.

［4］G.D.Forney，Jr.，Maximum-likelihood sequence estimation of digital sequences in the presence of intersymbol interference［J］.IEEE Trans.Inf.Theory，1972，18（2）：363-378.

［5］Maja Loncar，Fredrik Rusek.On Reduced-Complexity Equalization Based on Ungerboeck and Forney Observation Models［J］.IEEE.TRANSACTIONS ON SIGNAL PROCESSING，VOL.56，NO.8，AUGUST，2008.

［6］R.Schober，H.Chen，and W.Gerstacker.Decision-feedback sequence estimation for time-reversal space-time block coded transmission［J］.IEEE Trans.Veh，Technol.，2004，53（4）：1273-1278.

［7］J.Hagenauer and P.Hoeher.A Viterbi algorithm with soft-decision outputs and its applications［J］.IEEE.Global Telecommunications Conference 1989，Dallas，Texas，Nov，1989：1680-1686.

［8］KAZUAKI MUROTA，and KENIKICHI HIRADE.GMSK Modulation for Digital Mobile Radio Telephony［J］.IEEE.TRANSACTIONS ON COMMUNICATIONS，VOL.COM-29，1981（7）.

［9］GOTTFRIED UNGERBOECK.Adaptive Maximum-Likelihood Receiver for Carrier-Modulated Data-Transmission Systems［J］.IEEE TRANSACTIONS ON COMMUNICATIONS，VOL.COM-22，1974（5）.

［10］Michael J.Gertsman and John H.Lodge.Symbol-by-symbol MAP Demodulation of CPM and PSK Signal on Rayleigh Flat-Fading Channels［J］.IEEE TRANSACTIONS ON COMMUNICATIONS，1997，45（7）.

［11］A.Hafeez and W.E.Stark.Decision feedback sequence estimation for unwhitened ISI channels with applications to multiuser detection［J］.IEEE J.Sel.Areas Commun.，1998，16（9）：1785-1795.