船舶MEMS微惯导网络精度技术研究*
卢道华 张 竞
(江苏科技大学 镇江 212003)
1 引言
为了提高惯性导航系统的精度可以选用精度较高的惯性器件。但高精度的惯性器件的成本也高[1],为了保证一定精度的情况下降低成本文中提出了采用微惯导在船上进行应用性布置并将船舶上不同位置的MEMS惯导系统通过CAN总线,组成可以进行数据传输的网络;同时将一路高精度的主惯导系统也接入CAN总线网络中。这样主惯导系统的导航信息通过CAN网络传递给每个子惯导系统,子惯导可以利用接收到的主惯导信息对自身的姿态角误差进行估计[2],并用估计值来修正其姿态矩阵。
2 MEMS微惯导网络结构
按照实时修正误差角的要求,将各个子惯导系统和主惯导系统作为网络节点搭接在微惯导网络中,微惯导网络连接方式如图1所示。
为了保证各个子惯导系统之间以及每个子惯导系统和主惯导系统之间的数据能够同步采集,将子惯导系统和主惯导系统均连接到同步采集电路进行数据同步处理并加上时间信息。同步采集电路输出的数据经由数据转换器输出CAN格式[3]的数据再通过CAN总线传输,作为数据处理的上位机通过CAN通讯卡也接入CAN网络中。
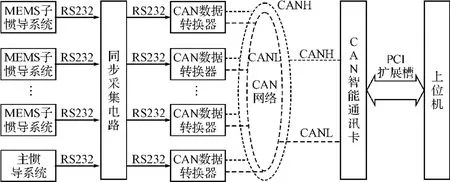
图1 微惯导网络系统结构图
3 MEMS微惯导系统误差模型
为了利用微惯导网络中的高精度主惯导对子惯性系统进行校正,需要先建立系统误差模型。
3.1 姿态角误差方程
由于主惯导系统精度远高于MEMS微惯导系统,因此主惯导系统的导航误差忽略不计[4~5],所以在以下论述中认为子惯导系统与主惯导系统之间误差角即为子惯导系统解算所得的导航坐标系与真实导航坐标系之间的夹角。设MEMS微惯导系统与主惯导系统之间的误差角为φ,定义矩阵

则姿态角误差方程可以表示为:

3.2 速度误差方程
理想状态下捷联惯导系统的比力方程为
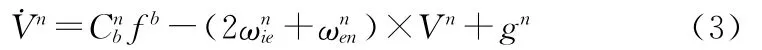
考虑微惯导网络系统的误差影响,按上式求得的速度也存在误差,设实际速度的计算值为Vnw,速度误差为δVn则有:

实际角速度为:

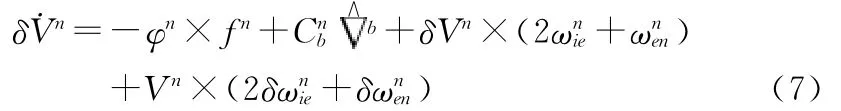
3.3 MEMS微惯导网络系统姿态角修正的状态空间模型
由于滤波估计时间短,陀螺仪和加速度计的器件误差在滤波估计过程中对姿态误差的影响很小所以陀螺漂移和加速度计零偏不引入状态空间模型,而是在数学模型中通过加大过程噪声加以等效。本文研究的模型将应用于舰船载体,而舰船载体的天向速度为零所以状态空间模型中也不引入此项。经过以上简化处理后的状态空间模型为
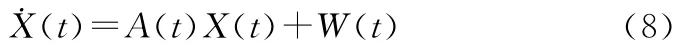
其中,系统矩阵

状态变量为X=[δVEδVNδφEδφNδφA]T,W(t)为系统过程噪声。
3.4 角速率匹配的量测方程
设MEMS微惯导系统陀螺仪输出的角速度为ωibs,其在MEMS微惯导解算的导航坐标系的投影为ωnsibs,主惯导陀螺仪输出的角速度为ωibm,由于假定主惯导系统已经实现精确对准[6~8],其导航解算所得的导航坐标系与当地地理坐标系重合,则主惯导陀螺仪输出的角速度在主惯导解算的导航坐标系的投影为ωnibm。
令观测量

量测方程可以表示为

其中量测矩阵为

U(t)为系统量测噪声。
4 利用卡尔曼滤波器估计误差角
将式(8)和式(11)离散化后,得到系统方程和量测方程的差分形式:

Kalman滤波基本流程如下[9]:
状态一步预测

一步预测误差方差阵

滤波增益矩阵
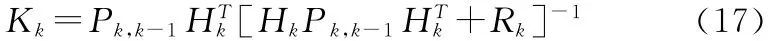
求解残差

状态估计
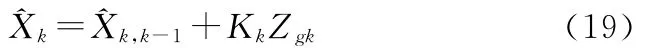
5 系统仿真分析
根据式(13)和式(14)并按照式(15)~式(19)的步骤用MATLAB软件编写仿真程序进行仿真运算。
5.1 仿真条件设置[10]
设置舰船摇摆模型为:
航向角θ=5°sin(2π/10×t)
俯仰角γ=15°sin(2π/6×t)
横滚角φ=10°sin(2π/8×t)
预设东向、北向、天向误差角分别为:0.5°、1.3°、0.75°

5.2 仿真结果及分析
图2至图4分别为东向、北向、天向误差角的卡尔曼滤波曲线,由图中可以看出三个方向的卡尔曼滤波曲线在15s后达到稳定,滤波时间小于15s,滤波估计误差不大于±1.8′。
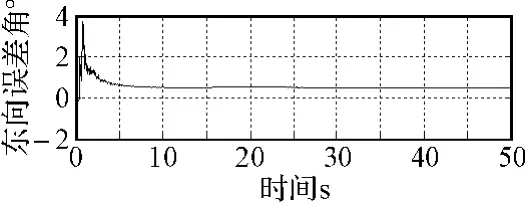
图2 东向误差角的卡尔曼滤波曲线
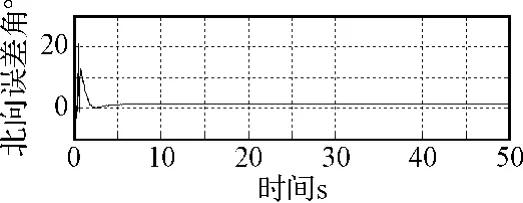
图3 北向误差角的卡尔曼滤波曲线

图4 天向误差角的卡尔曼滤波曲线
6 结语
针对由低成本MEMS器件构成的惯性导航系统精度低,导航误差随时间积累的特点,本文提出了通过船舶上的MEMS微惯导网络进行信息传输,利用船舶上高精度主惯导的导航信息来修正分布在船舶其他位置的MEMS微惯导系统的导航误差的方法。建立了适合误差角快速修正的五阶状态空间模型和以角速率为观测信息的量测矩阵,并根据以上数学模型设计了卡尔曼滤波器。在船舶典型摇摆情况下进行了50s系统仿真,仿真结果表明文中所采用的方法可以在较短时间内估计出误差角,仿真估计误差不大于±1.8′,滤波时间小于15s。
[1]马晓勇.微惯性测量组合标定技术研究[D].江苏科技大学工学硕士学位论文,2009,3.
[2]程向红,黄华.捷联惯性系统初始对准中IMU安装误差及陀螺漂移的估计与补偿[J].中国惯性技术学报,2004,12(5):13-16.
[3]铙运涛,邹继军,王进宏,等.现场总线CAN原理与应用技术[M].北京:北京航空航天大学出版社,2003.
[4]卢江涛,段立,罗兵.基于Unscented卡尔曼滤波的超视距目标跟踪[J].系统仿真学报,2007,19(7):1615-1616.
[5]鲁浩,杜毅民,王纪南.应用于近距空空导弹惯导系统的传递对准技术[J].中国惯性技术学报,2005,13(5):10-15.
[6]Jun.L,Kejie.L.Summarize of research based on MIMU integration storage test system[J].Proceedings of the International Symposium on Test and Measurement,2004:61-64.
[7]T Lefebvre,H Bruyninckx,J De Schutter.Comment on“A new method for the nonlinear transformation ofmeans and covariances in filters and estimators”[J].IEEE Trans.Automat.Contr.,2002,47(8):1406-1408.
[8]Sheimy N E,Nassar S,Noureldin A.Waveletde-noising for IMU alignment[J].IEEE A&E SystemMagazine,2004,19(10):32-39.
[9]付梦印,郑志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.
[10]傅群忠,薛晓中.基于新型滤波器-HABF的SINS传递对准仿真[J].中国惯性技术学报,2007,1(3):273-277.

