基于采样的非线性滤波算法比较＊

赵 侃 漆德宁

（解放军陆军军官学院 合肥 230031）

1 引言

由于非线性问题的复杂性，非线性估计难度较大。进行非线性估计的的最优方案需要得到其条件后验概率的完整描述，然而这种精确的描述需要太大的计算量而无法实际应用［1］，为此人们提出了大量次优的近似方法［2］，主要包括：对非线性函数进行近似，采用高阶项忽略或逼近措施；用随机采样方法近似非线性分布的概率密度；用确定性采样方法近似非线性分布；在非线性估计领域中使用递推的扩展卡尔曼滤波（EKF）方法通过对非线性函数的Taylor展开式进行线性化截断，从而将非线性问题转化为线性问题。但EKF只适用于滤波误差和预测误差很小的情况。否则，滤波初期估计协方差下降太快会导致滤波不稳定，甚至发散。

本文对近年来受到广泛关注的粒子滤波（PF）算法［3］和通过确定性采样点来近似非线性分布不敏卡尔曼滤波进行讨论。并通过仿真证明对于非线性程度高、模型复杂系统的估计问题本文研究的滤波算法能获得更精确的估计结果。

2 UKF算法

Julier提出了unscented卡尔曼滤波（UKF）算法［4～6］。其核心思想是UT变换，状态的概率密度分布可通过能完全表述密度函数的均值和方差的有限个样本点来描述，通过直接使用状态或测量的非线性方程映射这些样本点，加权求和得到更新的均值和方差，若将非线性方程采用泰勒级数展开式表示，可看出UKF方法将精确到与三阶泰勒级数展开式相当的均值和方差。

UKF算法流程如下：

Step1：初始化数据

Step2：通过非线性函数采样得到k＋1时刻的sigma采样点χk＋1，再由sigma点求取均值和方差。

Step3：计算量测采样点Zk＋1点及其预测值、协方差矩阵P。

Step4：计算状态向量和量测向量的协方差矩阵S。

Step5：计算滤波的增益值K。

Step6：计算状态向量的估计值＾xk＋1和方差Pk＋1。

在卡尔曼框架内应用UT技术就得到了UKF算法。

3 粒子滤波算法

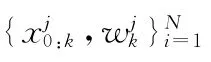
于是，就有了一种表示真实后验密度p（x0：k｜z1：k）的离散带权近似表示，而那些关于数学期望的复杂计算（通常带有复杂的积分运算）就可以简化为和运算，如

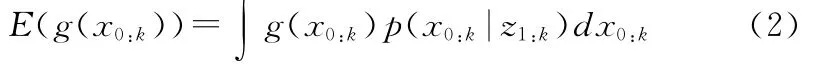
基本PF算法的一个主要问题是粒子退化，即经过几次迭代之后，差不多所有的粒子都具有负的权值。重抽样是解决退化问题的一个有效办法，依靠重采样，要求提议分布的设计尽可能逼近后验概率密度函数，选择和设计合适的次优提议分布一直是粒子滤波的研究重点之一。下面介绍一种基于不敏卡尔曼滤波提议分布的粒子滤波算法。

4 无味粒子滤波

在粒子滤波中，重要性密度函数的选择是关键技术之一，选择好的重要性密度函数可以大大降低粒子数目，上一节所研究的基本粒子滤波算法的基础上采用UKF滤波生成重要性密度函数，得到基于UKF的粒子滤波算法（UPF）［8～10］，其运算步骤如下

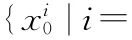
step2：For t＝1，2，…

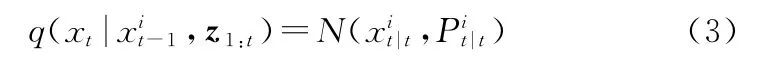
递归地计算每个粒子的重要性权值［7］，将各个粒子的权值归一化

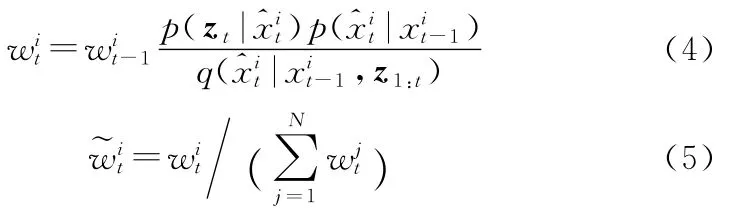
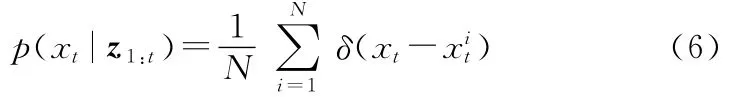
对于高维变量的估计，粒子滤波需要大量的粒子，所需的计算量巨大。本节中将UKF算法和PF算法相融合，形成了UPF算法。该算法思想采用UKF算法生成粒子滤波的提议分布，目的是能够融入当前观测的信息，以改善滤波效果。

5 实验比较与分析

本文对EKF、UKF、PF、UPF三种方法进行仿真实验，仿真环境如下：采用如下的非线性非高斯系统模型：

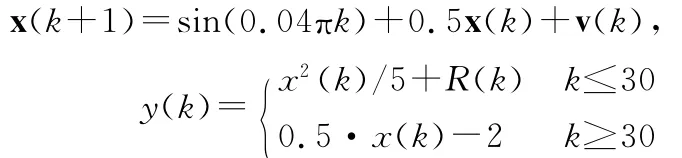
这里v（k）服从Gamma（3，2）分布，观测噪声R（k）服从高斯分布 N（0，10－5），目标的初始状态x（0）＝20，经过100次蒙特卡罗仿真，每次仿真时间是60s，采样间隔为1s。

在上述条件下，对各种滤波算法分别进行50次Monte Carlo仿真。为了清晰显示各种滤波器的估计结果，图1、图2显示了在不同初始误差情况下，各种滤波算法对目标目标位置估计的误差。

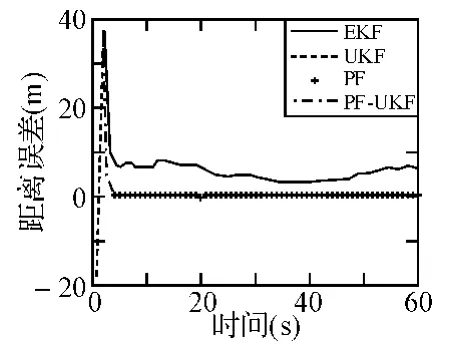
图1 各算法的位置估计误差（v（k）分别服从Gamma（3，2）

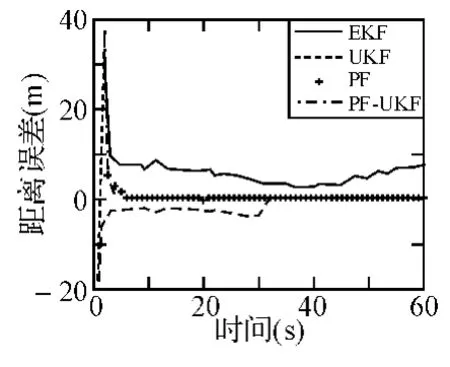
图2 各算法的位置估计误差（v（k）分别服从Gamma（9，6）

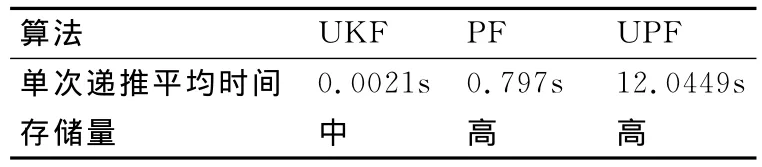
表1 滤波器运算效率比较

由图1、图2看出，各种滤波器都是渐进无偏的。UKF和PF，收敛速度最快、估计精度最高；EKF性能逊于UKF和PF，大约60s收敛到无偏位置，UPF由于粒子数不足，估计误差曲线抖动较大；而UKF没有出现滤波发散、丢失目标的现象。当增大初始误差时，PF的收敛速度最快，UKF在起始阶段滤波精度较低，但随着时间增加其滤波精度与PF基本相同。

由表1可以看出，UKF运算效率最高；PF次之，UPF的运算时间约是UKF的5800倍。粒子滤波器已经不能实时对目标进行跟踪。

6 结语

综合考虑各种非线性滤波器的收敛速度、运算效率等因素，在初始误差较小的情况下，UKF比PF具有更高的跟踪精度，收敛更快，而在初始误差较大的情况下，PF收敛速度更快，这可以赢得更多的预警时间。PF和UPF运算量巨大，无法实时跟踪目标，而且需要更多的变量存储空间。在目标跟踪应用环境下，如果比较准确，过程噪声较小的模型，UKF已经足够精确，而PF在粒子数有限（本文中PF选用200个粒子）的情况下不能提高估计精度，因此，随着计算机能力的不断提高，PF将具有广泛的应用空间。

［1］Daum F E.Nonlinear filters：Beyond the Kalman Filter［J］.IEEE AES Systems Magazine，2005，20（8）：57-69.

［2］Li X R，Jilkov V P.A Survey of Maneuvering Target Tracking Approximation Techniques for Nonlinear Filtering［J］.Proc.Of the SPIE，2004，5428：537-550.

［3］Zhao Huibo，Pan Quan.PF-UKF-RJMCMC Approaches for Radar Target-Tracking［J］.International Conference on Information Technology and Computer Science，2009：273-374.

［4］Xiong K，Zhang HY，Chan CW.Performance Evaluation of UKF Based Nonlinear Filtering［J］.AUTOMATICA，2006，2（42）：261-270.

［5］Julier S J，Uhlmann J K.Unscented Filtering and Nonlinear Estimation［J］.Proc.IEEE，2004，92（3）：401-422.

［6］Van Zandt J R.Boost Phase Tracking with an Unscented Filter［J］.Proc.Of the SPIE，2002，4728：263-274.

［7］Andreas N S.Space-Based Infrared System（SBIRS）System of Systems［J］.IEEE Aerospace Applications Conf.Proc.，1997（7）：429-437.

［8］Hol J.D，Schon T B，Gustafsson F.On Resampling Algorithms for Particle Filters［J］.IEEE Nonlinear Statistical Signal Processing Work-shop，SEP 13-15，2006：79-82.

［9］Sanjeev M，et al.A tutorial on particle filters for online nonlinear non-Gaussian Bayesian tracking［J］.IEEE.Trans.SP-50，2002（2）：174-188.

［10］Ito K，Xiong K.Gaussian Filters for Nonlinear Filtering Problems［J］.IEEE Trans.Automatic Control，2000，45（5）：910-927.