并联有源滤波器网侧谐波电流反馈控制

孙孝峰 曾 健 李宁宁 李 昕

（燕山大学电气工程学院电力电子节能与传动控制河北省重点实验室 秦皇岛 066004）

1 引言

电力电子技术的快速发展给人们生活带来便利的同时也给电网带来了越来越严重的谐波污染，有源电力滤波作为一种谐波抑制技术也因此得以重视[1]，其中并联型有源电力滤波器 (Shunt Active Power Filter，SAPF) 的应用最为广泛。

SAPF可以检测补偿对象电压[2]或检测补偿对象电流[3]计算指令电流，常见的SAPF电流检测有负载端电流反馈控制法、网侧电源端电流控制法以及两者的复合控制法。就补偿效果而言，网侧电流反馈优于负载端电流检测法[4]。网侧电流反馈方法因电源电流反馈而构成闭环控制系统，它把产生谐振的传递函数包括在闭环内，选择适当的校正环节就可以抑制谐振，但如果校正环节的放大倍数过大会使系统不稳定[5,6]。文献[4]对含有网侧电流反馈的复合控制SAPF进行了建模和稳定性分析，通过加入相位超前校正环节提高了系统稳定性，改善了补偿效果。该方法可以提高系统稳定裕度，进而提高闭环增益上限，但是补偿效果并不随相位裕度和闭环增益的增加而一直提高，反而在一些情况中下降，本文分析得出该问题存在的根本原因，在系统中采用选择性谐波检测方案以提升其补偿效果。

2 网侧电流反馈系统

网侧电流反馈方式的指令电流和网侧谐波电流iSh关系为*CShi=ki，理论上k=1时谐波得到完全补偿。图1是本文分析和实验的三相三线电路结构原理图，其中iS为网侧电源电流，iL是负载电流，iC是补偿电流。对于节点A，iCL=iL-iC，系统数学模型框如图2所示。

图1 并联型有源滤波器系统结构Fig.1 SAPF system structure block

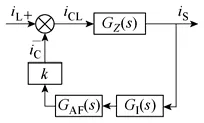
图2 系统数学模型框图Fig.2 Mathematical model of system

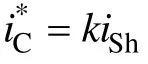
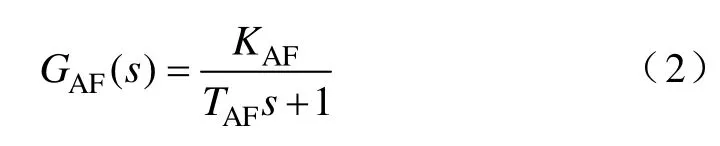
系统开环传递函数如下：

图3 电流iCL到iS的等效电路Fig.3 Equivalent circuit from iCL to iS

3 网侧谐波选择性滤波器复合比例环节反馈

网侧谐波电流反馈因其直接抑制网侧谐波电流而效果优于负载谐波电流反馈，但其稳定性较差。图4为k=1时系统开环伯德图，幅频为正时，相频曲线就穿越了－180°线，系统已经不稳定，另外幅频特性在低频段约400Hz处有一个谐振峰值，在此频段负载谐波流向电网时被放大，使得电网电流波形发生畸变[5]。文献[4]应用相位超前校正环节如式（4）所示。为获得良好的补偿特性，G(s)应有较大的放大倍数M，以增大系统的开环增益，但放大倍数M过大会使闭环系统不稳定[5]。

图4 系统开环伯德图(k=1)Fig.4 Bode diagram of open-loop system (k=1)

令K=kM，加入校正环节后系统结构图如图5所示。图6a是K=4，T分别取0.1ms、0.3ms和0.5ms校正后结果和校正前的对比，校正后相位裕度随T减小而增加，低频段幅值增益却减小；图6b为T=0.3ms时K=4、6、8时的情形，K=8时系统相位裕度已经降到4，无法满足系统对稳定裕度的要求。

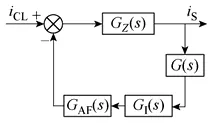
图5 加入相位超前校正环节系统框图Fig.5 Diagram of system with phase lead correction

图6 加入校正环节效果比较Fig.6 Comparison of corrected results

从以上分析可知，加入校正环节后K值有所提高，且T越小K取值越大。但一味减小T追求K值的增大是没有意义的，减小T值增加稳定裕度的同时系统的低频段增益降低，导致对含量较大的低频谐波抑制作用降低，这是阻碍补偿效果进一步提高的主要原因。

由上面分析可知，在提高相位稳定裕度的同时，低频段的增益也要提高，才能提高补偿效果。选择性滤波在低频段特定频率处提高幅值增益，可以达到提高低频段增益的目的。选用运算较简单的在静止坐标系等效瞬时无功功率理论，其传递函数如下[6]：

可见该传递函数形式是带通滤波器（BPF），取npk=0.5，Ak=20，φk为零时选择5、7次谐波，离散化传递函数为

将式（6）串入系统环路中，系统开环伯德图如图7所示，该系统在低频段5、7次特定频率处幅值增益得到提高，系统却再次不稳定，因为该系统的谐振频率较低，带通滤波器的高频段相位延迟导致系统不稳定，需要重新设计带通滤波器，使其高频段相位延迟为零。

图7 选择性滤波器的接入后的系统伯德图Fig.7 Bode diagram of system with selective filter

进一步采用“BPF＋N”的形式，即在原来的传递函数基础上加常数N。改进后的传递函数与原来伯德图对比如图8所示，BPF＋1与BPF相比在低频和高频段的相位延迟都变为零，图8中BPF＋1形式目的在于提取5、7次谐波，低频段其他频次谐波幅值增益为零，即对其他成分的谐波几乎无影响。BPF＋1串入系统后效果如图9所示，通过改进使系统的稳定裕度和低频段5、7次谐波的增益都满足了要求，框图实现如图10所示。

图8 BPF与BPF+1的伯德图对比Fig.8 Comparison of BPF and BPF+1 bode diagram

图9 BPF＋1的形式串入后的系统伯德图Fig.9 Bode diagram of the system with BPF+1

图10 改进后的系统框图Fig.10 System diagram after improved

4 实验验证及结果分析

根据图1中原理电路搭建实验平台，进行了实验研究，实验中主要参数如下：

实验采用TMS320F2407DSP进行数字信号处理，谐波电流发生器采用重复控制[7-9]，采样频率为3.2kHz，对20次以下谐波处理[10]，交流测电感L为3.5mH，采用二极管整流桥带阻性负载作为非线性负载，低频段对5、7次谐波进行选择性滤波。

图11验证了电源端电流检测SAPF系统，无相位超前稳定性校正时，闭环增益只能为0.5，当k取1时系统不稳定。图11～图14波形1均为补偿后电源电流 (2A/格)，波形2均为补偿电流 (1A/格)。

图11 系统稳定性校正前的实验波形Fig.11 Experimental waveform before phase lead correction

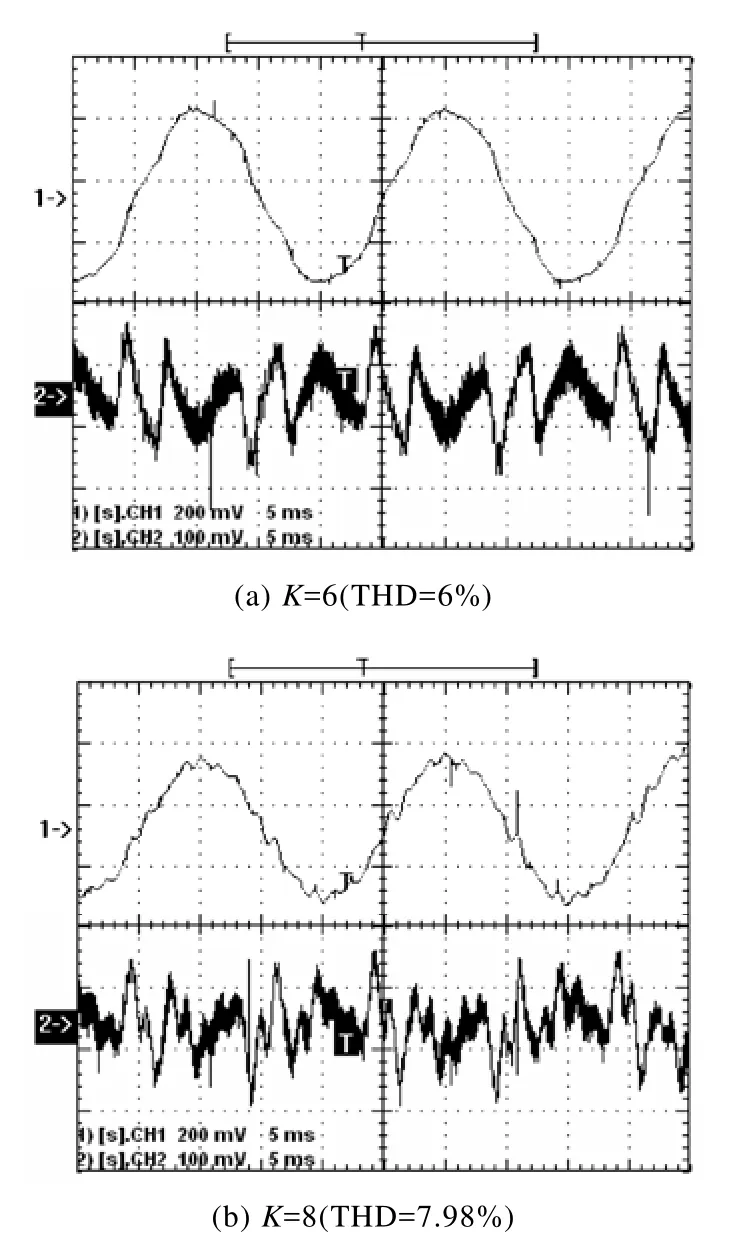
图12 相位超前校正T=0.3ms的补偿效果Fig.12 Compensation effect of phase lead correction when T=0.3ms

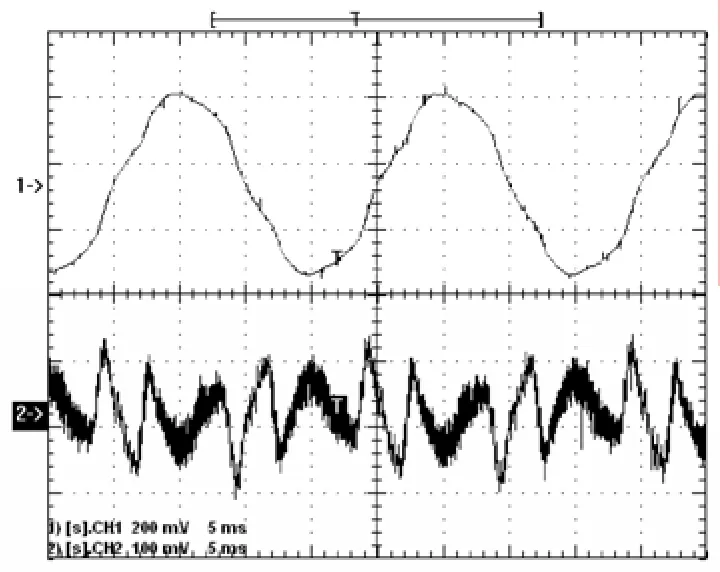
图13 相位超前校正T=0.2ms，K=8补偿效果(THD=6.57%)Fig.13 Compensation effect of phase lead correction(T=0.2ms)

图14 在T=0.3ms，K=6基础上串入BPF（Ak＝20）Fig.14 Waveform with BPF (Ak=20) based on T=0.3ms,K=6

图15 在T=0.3ms，K=6基础上串入BPF+6（Ak＝20）(THD=2.52%)Fig.15 Waveform with BPF (Ak=20) based on T=0.3ms,K=6 (THD=2.52%)

图12 a、图12b分别给出T取0.3ms时K=6、K=8的实验波形，当K值增加到8时已经开始出现不稳定的迹象；图13是T为0.2ms，K=8时的实验波形，系统再次稳定，这次的K值提升并没有带来补偿效果的改善，电流THD由6%增加到6.57%，即相位超前校正对幅值增益的提高是有限的。

图14为串入BPF后的实验波形，与理论分析一致，由于其高频段相位延迟导致系统不稳定。图15是串入改进“BPF+6”形式的实验结果，从上到下波形是：SAPF接入点电压(50V/格)，补偿后电源电流(2A/格)，补偿前电流(2A/格)，谐波发生器电流(1A/格)，相对于相位超前校正，补偿后电源电流THD降到2.52%，补偿效果明显提升。

另外值得一提的是，文献[7]中提到有源滤波的选择性闭环补偿方法有补偿频率上限，即在电路中存在容性器件时会和线路感抗谐振导致谐波放大，补偿频率必须小于此谐振频率，谐振频率较低时会严重影响补偿效果。本文中的谐振在7次谐波频率附近，通过本文的方法依然得到了良好的补偿效果。

5 结论

通过对闭环并联型有源滤波器数学模型分析，相位超前校正环节增加稳定裕度同时降低了低频段增益是影响网侧谐波电流反馈控制的有源滤波器稳定性的原因。应用选择性谐波检测提高低频特定谐波增益，该系统在低频段特定频率处幅值增益得到提高，但其高频段相位延迟导致系统再次不稳定，而采用复合“BPF+N”，改进后的选择性谐波检测函数消除了高频相位延迟，并保证了5次、7次等附近频率的低次谐波增益，适合网侧谐波电流反馈控制。

[1] Singh.B,Al Haddad K,Chandra A.A review of active filters for power quality improvement[J].IEEE Transactions on Industrial Electronics,1999,46(5):960-971.

[2] Nagaraju Pogaku,Tim C.Green.Application of inverter-based distributed generators for harmonic damping throughout a distribution network[C].IEEE Power Electronics Specialist Conference,2005,36:1922-1927.

[3] Paolo Mattavelli,Fernando Pinhabel Marafa.Repetitive control based for selective harmonic compensation in Active Power Filters[J].IEEE Transactions on Industrial Electronics,2004,51(5):1018-1024.

[4] 颜晓庆,杨君,王兆安.并联型电力有源滤波器的数学模型和稳定性分析[J].电工技术学报,1998,13(1): 41-45.Yan Xiaoqing,Yang Jun,Wang Zhaoan.The mathematical model and stablity anasylis of shunt active power filter[J].Transactions of China Electrotechnical Society,1998,13(1): 41-45.

[5] 王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].2版.北京: 机械工业出版社,2005.

[6] Paolo Mattavelli.A close-loop selective harmonic compensation for active filter[J].IEEE Transactions on Industry Applications,2001,37(1): 81-89.

[7] 耿攀,戴珂.三相并联有源电力滤波器电流重复控制[J].电工技术学报,2007,2(22): 127-131.

Geng Pan,Dai Ke.The repetitive control algorithm based current waveform correction for shunt active power filter[J].Transactions of China Electrotechnical Society,2007,2(22): 127-131.

[8] 游志青,胡育文.采用重复控制技术的逆变器仿真研究[J].电工技术与自动化,2002(2): 37-40.

You Zhiqing,Hu Yuwen.Simulation of repetitive controller’s coefficient in inverter[J].Machine Building &Automation,2002(2): 37-40.

[9] Juha Kauraniemi,Timo I Laakso,Iiro Hartimo.Delta operator realizations of direct-form IIR filters [J].IEEE Transactions on Circuits and Systems-II,1998,45(1): 41-52.

[10] Isabel Deslauriers,Nysret Avdiu,Boon Teck Ooi.Naturally sampled triangle carrier PWM bandwidth limit and output spectrum[J].IEEE Transactions on Power Electronics,2005,20(1): 100-106.