基于区域增长和三角分割的局部纹理映射算法
申世恒, 李柏岩, 刘晓强, 王府梅, 宋 晖
(1.东华大学 计算机科学与技术学院,上海 201620;2.东华大学 纺织学院,上海 201620)
在进行三维虚拟物体展示时,通常采用真实二维图像作为贴图,通过纹理映射技术将其映射到三维物体模型表面,从而增强三维场景中虚拟物体的真实感。纹理映射通常是针对一个对象,整体进行映射的,但在一些情况下,纹理映射只针对对象上一个小区域进行,称局部纹理映射。例如,在进行织物虚拟展示时,需要对展示物指定位置进行局部修饰、添加提花图案等。
针对如何将一张贴图恰当地映射到三维模型指定的局部区域的问题,文献[1]提出了基于极坐标的方法,以三维物体上一点为中心,在保证与其邻接点的方向和距离不变的情况下,求出邻近点的纹理坐标,并以邻接点为中心点,继续向周围邻接点进行扩展,保证纹理不会发生严重的扭曲;文献[2-3]提出中心扩散的方式,以一个种子面开始,采用广度优先搜索方法扩散确定局部映射区域,该方法需手动控制映射区域,不能自动控制纹理映射区域,并且在局部细节处理上效果不太理想;文献[4-6]提出基于中间面的方法,通过控制中间面,达到局部纹理映射的效果。该方法对于规则化的三维物体能给出很好的映射效果,但对于非参数化的不规则三维物体则不能保证很好的映射。关于纹理合成方法,文献[7]提出一个快速有效的纹理合成方法,为局部纹理映射提供一种很好的拼接方法;文献[8]提出一种图像修复算法,实现对纹理失真的修复。
三维模型一般采用三角面为基本单位来进行逼近模拟。本文也以三角面为基本的映射单位,通过选定一个基准点,构建一个基准面,采用向周围点进行扩张的方式,确定局部映射区域。对于相对较大的三角面片,采用一定的算法对其进行分割,以控制区域映射有效范围,防止过度映射的出现。
1 顶点纹理坐标化
为将纹理映射到三维模型上,首先需要给模型的每一个顶点都分配一个合适的纹理坐标。本文采用平面展开法,即通过选定基准点,并以此基准点所在平面作为一个基准面,将此基准面周围包含基准面顶点的三角面展平到此平面上,再计算每个顶点到基准点的距离和方向,实现三维顶点的纹理坐标化。
假设三角面PAB以顶点P为原点,对应纹理中心坐标点,以顶点P所在的一个面(设为T)为基准面。对于所有包含顶点P的面上的顶点,利用下面介绍的方法,计算出各个点所对应的纹理坐标。
选取包含顶点P的三角面T作为基准面,搜索模型中所有包含顶点P的面,对于其中任意一个面,及其面上的非P点的顶点A,计算出向量在平面T上的投影点A′,以及向量的模,然后利用、向量,以及用于控制纹理方向的纹理正向向量Qmap,求出A点的纹理坐标。而对于三角面上另一顶点B,可以计算向量之间的角度α以及的模,即可以利用α求出B点在平面T上所对应的B′及其纹理坐标。通过已计算出纹理坐标的顶点,再以此顶点所在面为基准面,此点为基准点,采用相同的方法计算出其周围顶点的纹理坐标,实现顶点纹理坐标化。
首先需要确定用于纹理映射的基准平面。假设用来确定基准平面的方程为:
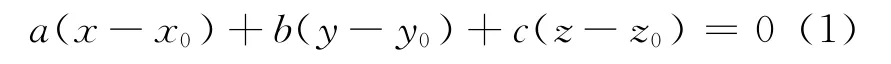
已知A点坐标(x1,y1,z1),面法向量为(a,b,c),设A′坐标为(x2,y2,z2)。通过求解联立方程,即
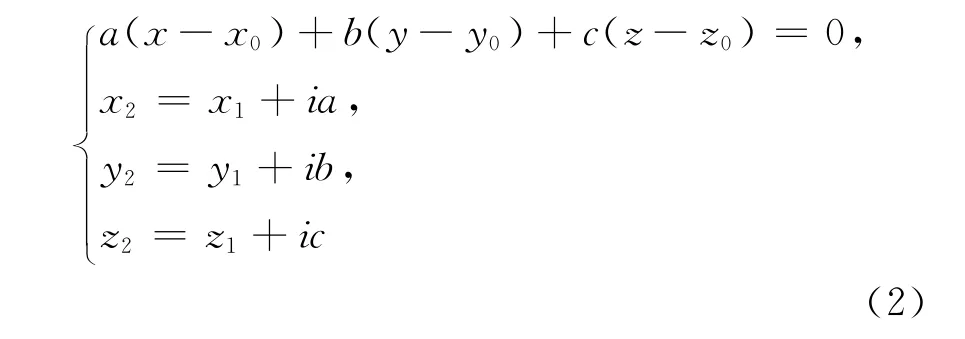
可以得出i,从而求得A′的三维坐标(x2,y2,z2)。
其次计算模型上相关点的纹理坐标。通过计算点A′在平面T的坐标,可以计算向量,假设与纹理正向向量Q夹角为θ,通过余弦
map定理可求出夹角的正弦与余弦值,即

2 确定映射区域
确定映射区域是实现局部纹理映射的关健。通过上述方法,可以将三维点展平在一个平面内,并计算出各点对应的纹理坐标。在这个平面内,以原点为圆心,纹理半径R做圆,圆内覆盖的面,即为所要进行映射的面。其中R的大小可在交互操作时由用户确定,同时为了避免重复计算,通过记录已映射的点与面,在进行映射域扩展过程中,对新扩展的面进行判断,以使计算工作量最少。算法过程如下:
(1)建立容器V-Vert、V-Face和V-In,分别用来存储已坐标化的点、已映射的面和包含在映射范围内的点。选择一个初始点作为中心点,加入到V-Vert中,并将此初始点纹理坐标设为(0.5,0.5),并添加到 V-In中。
(2)搜索V-Vert,采用宽度优先搜索法,当V-Vert不为空时,取其中的第1个点。
(3)如果这个点在V-In中,对包含此点的面,若该面不在V-Face中,则利用前面介绍的方法,对面上的点进行纹理坐标化,并将这个面中没有出现在V-Vert中的顶点加入其中,将该面加入V-Face中。对于任意一个已经进行了纹理坐标化的顶点,记其纹理坐标为(xv,yv),如果该纹理坐标满足公式R,则将该点加入容器V-In中。
(4)如果这个点不在V-In中,对于包含此点的面,若该面不在V-Face中,则进行映射,并对面上其余点进行纹理坐标化,并把这些点加入V-Vert,把含有选定点的面记入V-Face。
(5)将该点从 V-Vert中删除,返回步骤(2)。
重复执行步骤(2)~(5),直至 V-Vert为空。根据这个方法,可以避免重复计算,并将纹理映射范围圈定在一个合理的范围之内,以达到一个较好的局部纹理映射效果。
在进行上述步骤的过程中,为避免将三角形都展开在一个平面所带来的变形问题,本文采用局部平面展平法。对于选定的一个点,以其所在的一个平面作为基准面,对每一个包含此点的三角面,取其法向量,并求取这些法向量的平均值作为法向量,并基于此点做基准面[2],然后将各个三角面展平到此基准面上。利用上述方法进行扩展后,对于每一个扩展后并被选为新的基准点的点,以此点所在的一个平面为新的基准面,再将包含此点的三角面依次展平到此基准面上。如此循环,直到满足上述条件中的终止条件为止。
通过局部展平法,对于每一个点计算出来的纹理坐标,其到达基准点纹理坐标的距离为绝对距离,其到达中心点坐标的距离也为绝对距离,因而贴图在纹理映射后变形很小。
3 三角面剖分
对三维物体进行纹理映射时,通常以三角面为基本映射单位进行映射。在局部映射的过程中,对于一块三角面片,可能只需对一小部分区域进行映射,若将整个面片进行映射,则会出现过度映射的现象。可能出现的情况可分为3种,如图1所示。
(1)情况1。如图1a所示,假设点O为纹理中心,圆环为纹理映射区域所覆盖区域,若采用基于三角面为基本单位的映射,则A、B、C、D和E点均会被覆盖在映射区。随着纹理映射区域变小,映射的效果会变得越来越不理想,且会出现过度映射现象。
(2)情况2。如图1b所示,纹理中心及覆盖区域落在一个大的三角形内,与第1种情况类似,随着圆区域覆盖面积变小,也会出现过度映射状况。
(3)情况3。如图1c所示,因三角形ADC不在需要被映射范围之内,这样会造成局部纹理映射不完整,而即使加上ADC到映射区域,也会出现过度映射的状况。
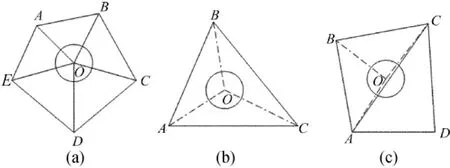
图1 确定局部纹理映射区域
对于上述情况,本文提出了一种通过交点求切线的方法,细化映射区域,如图2所示。

图2 用切线找到特征点
(1)如图2a所示,纹理边界与三角面中的2个边会有2个交点,以这2个点分别做圆的切线,再从圆边上取一点做切线,该切线与三角面的第3条边平行,并且与上面2条切线相交,取相交点为2个特征点,并且取圆与2边的交点为2个特征点,加上原点5个点为特征点进行三角剖分。这5个特征点分别对应5个纹理坐标。
(2)对于第2种情况,可以从圆心到三角面在3个顶点进行三角剖分。如图2b所示,剖分后的结果与第1种情况类似,可以使用方法(1)进行再次剖分。
(3)对于第3种情况,如图2c所示,首先判断ACD面是否需要映射,判断依据是圆心到边上的距离是否小于半径。若该面需要进行映射,除圆与边的交点做切线外,寻找一条边与该边平行的切线,与另外2条切线相交的点,取为特征点,其后剖分的情况与前2种相似。
以图2a为例进行推导。设圆公式为:
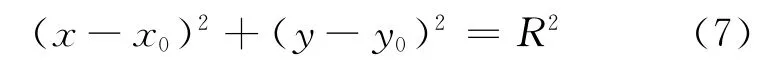
已知A和O的坐标,可求出直线AO方程:
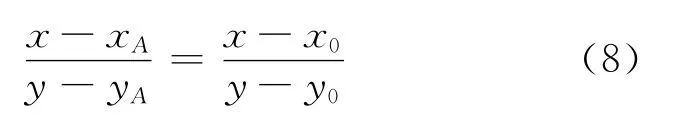
联立(7)式和(8)式,即可求得F点坐标(xF,yF),并以同样的方法,可以求得G点坐标(xG,yG)。
已知圆方程及F、G点坐标,可以求出圆上F、G点切线方程如下:
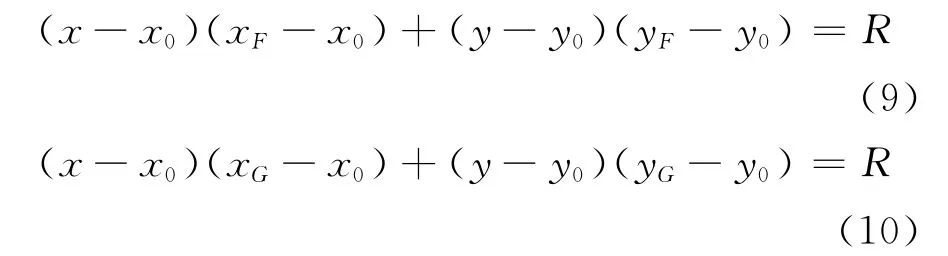
通过A点和B点可以求出切线HI方程,设
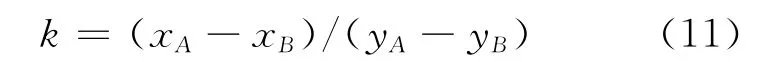
切线HI方程为:

联立(9)式、(12)式及(10)式、(12)式即可求出H点及I点坐标(xH,yH)和(xI,yI)。
通过上述过程,可求出O、F、G、H、I各点的坐标,并通过文中所述的逆方法,求出各点对应的三维空间坐标,通过这5个特征点进行三角剖分后再进行纹理映射,达到预期效果。
可以证明在取最少特征点的情况下,经过这样的三角剖分后,可以保证局部纹理会被全部映射。而且,所有映射区域内,都不会出现过度映射的情况。
4 实验效果及分析
为了说明上述算法的实际效果,本文在VC++编程环境中使用Open GL图形库构造三维场景环境,通过在一个针织袜子上映射提花图案,演示局部纹理映射和三角剖分的效果。纹理贴图采用大小256×256像素的BMP文件。
在指定的纹理映射区域与模型中三角面片之间比例较大时(一般情况),使用本文的局部纹理映射算法实现映射的效果如图3所示。显然,算法能够有效地实现局部区域内的纹理映射。

图3 一般情况下本文算法的映射效果
在指定的纹理映射区域与三角面之间比例较小时,若不进行三角剖分,纹理映射效果往往如图4所示。显然,由于构成物体模型的三角面片大小不一,在尺度上很接近于贴图,基本上无法找到适合贴图大小的映射区域,因而无法恰当地映射贴图,产生图4所显示的现象。
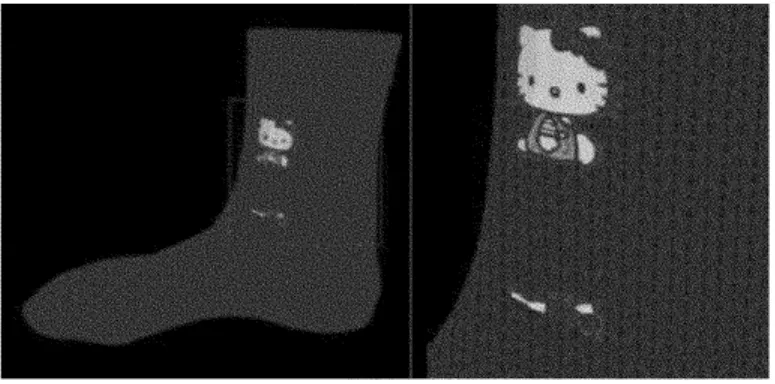
图4 无三角剖分时映射效果
采用本文算法对大的三角面片进行三角剖分后,可得到图5所示的映射效果图。由于剖分得到更小的三角面片,能更精确地构建映射区域,从而得到较好的局部纹理映射效果。

图5 有三角剖分时的映射效果
本文的一般算法与三角剖分算法时间复杂度均为:T(n)=O(nm),其中m为纹理覆盖的三角面数。三角剖分算法较一般算法计算时间略微有所增加,但由于局部纹理映射的范围一般比较小,纹理贴图覆盖的三角面数非常有限,因此算法仍然能够满足实用要求。
5 结束语
本文通过局部平面展平法进行纹理坐标计算,可以有效地减少二维纹理贴图映射到三维物体上变形,通过顶点扩张的方法,将纹理映射区域限制在一个合理的范围之内,并通过三角剖分,避免了因纹理映射区域与所在三角面片尺度太接近所带来的过度映射问题,有效地保证了局部区域纹理映射效果。本文提出的算法成功地运用于虚拟针织织物的修饰和提花设计中,同时,对于其他类似的虚拟仿真应用也具有实用价值。
[1]Ryan S,Cindy G,Brian W.Interactive decal compositing with discrete exponential maps[J].ACM Transactions on Graphics(TOG),2006,25(3):605-613.
[2]刘小丹,曾玲玲,孙红岩.中心扩散法局部区域纹理映射[J].计算机工程与设计,2010,31(17):3852-3855.
[3]Hormann K,Levy B,Sheffer A.Mesh parameterization:theory and practice[C]//International Conference on Computer Graphics and Interactive Techniques,2007.
[4]江巨浪.多面体表面局部纹理的映射方法[J].安庆师范学院学报:自然科学版,2003,9(2):61-64.
[5]黄 燕,王美清.基于立体投影算法的局部球面纹理映射技术[J].东莞理工学院学报,2009,16(5):49-54.
[6]张英杰,赵汝嘉,李永红.基于中间曲面的局部纹理映射技术[J].西安交通大学学报,1997,31(7):110-113.
[7]薛 峰,张佑生,江巨浪,等.一种快速、有效的纹理合成方法[J].合肥工业大学学报:自然科学版,2005,28(11):1361-1364.
[8]檀结庆,汪忠庆.新的基于邻近像素点的图像修复算法[J].合肥工业大学学报:自然科学版,2006,29(9):1072-1076.

