基于时间扭曲图快速搜索的运动融合方法

郑利平， 夏新宇， 王玉培

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

随着信息技术的飞速发展，三维动画正在逐渐成为继声音、图像、视频和三维模型之后的第5种多媒体类型［1］。作为三维动画的重要组成，角色动画在影视制作、计算机游戏等应用领域占据越来越重要的地位。为了得到形象逼真的角色动画，艺术、设计与计算机等领域的专家提出了很多的方法［2］。当前最流行的是一种骨骼动画制作方式，将角色抽象成具有层次结构的虚拟骨架结构，在角色网格和相应骨架之间建立蒙皮约束关系，并通过运动数据驱动骨架，产生角色动画［3］。

角色动画制作目前主要有手动设置关键帧和基于运动捕捉设备2种方法［4］。这2种方法生成动作序列都费时费力，因此如何能够重用这些数据，并在此基础上派生出更加丰富多样的运动，是当前计算机动画领域研究的重要内容之一，运动融合是运动重用的一个重要手段之一，该技术能够根据多个已经存在的运动数据，通过一定的手段，将它们的数据叠加在一起［5］。融合运动继承了原运动序列的主要特征，并且能够在各个运动之间平滑过渡［6］。

本文提出一种基于时间扭曲图快速搜索的运动融合方法，通过对动态时间扭曲（Dynamic Time Warping，简称DTW）加以一定规则的约束，快速地找到对齐帧，构造出运动序列之间的时间扭曲图，实现不同运动序列的时间配准以及对应姿态的融合。实验结果表明，该方法提高了搜索的效率，有很好的视觉效果，而且具有很好的灵活性和实用性。

1 相关工作

从技术的角度，当前对运动融合的研究主要可分为2类：

（1）信号处理方法。文献［7］在频域中采用傅里叶分析技术对运动数据进行内插和外插的方法，对真实的运动数据作傅里叶展开，来实现对运动的插值，其关节角的轨迹使用频域中的傅里叶来表示。文献［8］使用时空优化的方法，最小化关节角的转矩，实现一个运动片段到另一运动片段的过渡。文献［9］将运动看成信号，采用多分辨率运动过滤、时间变形、多目标运动插值、运动波形变换和偏移映射等运动信号处理方法，对运动数据进行混合，生成各种多样化的运动。

（2）参数化实例运动方法。该方法的主要思想是先使用权值计算函数量化运动实例，然后在此基础上对运动库中的运动序列混合、过渡等。该方法主要经历了2个阶段：① 使用权值计算函数量化运动实例，来生成连续的运动序列［10］，并在此基础上使用运动图的方法实现运动的过渡。由于采用的权值计算函数较为随意，计算出的权值与实际期望的权值可能有较大的差异，因此生成的运动不逼真；② 在以往研究工作的基础上，文献［11］采用改进的权值计算函数，使得运动实例的权值计算更准确，与实际期望的权值更接近。

动态时间扭曲最早应用在语音识别中，该算法基于动态规划（Dynamic Programming，简称DP）的思想，解决了发音长短不一的模板匹配问题，是语音识别中较为经典的一种算法，一些研究学者将DTW算法应用于运动融合领域。文献［9］中创建一个距离矩阵栅格，采用全局优化算法计算得到一条最优路径，但是该方法时间复杂度非常高，是输入运动序列帧数的指数级。文献［11］为了避免求解的复杂度，对DTW做了改进，并通过固定一些较为重要的关节的权重值，生成了更加平滑的运动。可以认为将DTW算法应用到动作序列对齐就是要寻找一个最佳的时间规整函数，使运动片段A的时间轴i非线性映射到运动片段B的时间轴j，并使总的累积失真量最小［12］。

如果源运动序没有相似的周期性和对应关系，比如骑马和芭蕾2个动作，则融合出新的运动序列是毫无意义的。因此，本文只考虑运动融合后能产生有实际意义的动作，即具有一定相似性的源运动序列。相似运动可能会有不同的时间分布。例如，在行走运动中，连续2次脚着地的时间间隔明显比跑步运动中的脚着地时间长得多。所以，对于2个运动序列必须进行相应的拉伸或缩短以使得对应帧匹配。在运动融合过程中，帧对应关系对于生成的最终融合运动效果十分重要，如果没有建立合适的帧对应关系，就无法得到自然协调的融合效果［13］。而时间扭曲（Time Warping）可使2段运动序列的帧之间建立一一对应关系，且具有相同的持续时间，从而使融合后的运动更加协调、自然。

一般来说，使用DTW算法在寻找对齐帧时运算量较大而且时间复杂度很高，因此提高对齐的效率是很有必要的。根据融合运动序列的特征，本文对DTW算法搜索对齐帧做了改进，因为运动序列具有一定的相似性，可以采用局部搜索的方式，再给予一定的规则约束，构造时间扭曲曲线，降低求解的时间复杂度。本文通过计算帧间距找出2段运动序列中的相似帧，再由相似帧构造时间扭曲曲线C（v），建立帧对应关系，对应帧的姿态融合，并重构根关节的运动轨迹。

2 动态时间扭曲

2.1 计算帧间距

文献［11］定义了一种帧间距计算公式，依此判断两帧的相似性，但是该距离公式以关节在世界坐标系的位置为度量标准，因此受角色根关节运动轨迹的影响，从而使得计算误差较大。为了克服以上不足，本文以关节旋转变化计算帧间距，将帧间距计算局部化；而且本文的运动信息是以四元数表示的，因此可以很方便地用四元数夹角表示关节旋转变化。

一个有m个关节的角色，计算其运动中2帧Μi、Μj的帧间距D（Μi，Μj），方法如下：

（1）分别以Μi、Μj为中心提取相邻的2W＋1帧，即窗口大小为2W＋1，如果窗口中的帧数小于2W＋1，则以中心帧填充之。

（2）任意2帧Μi、Μj的姿态距离P（Μi，Μj）定义为：

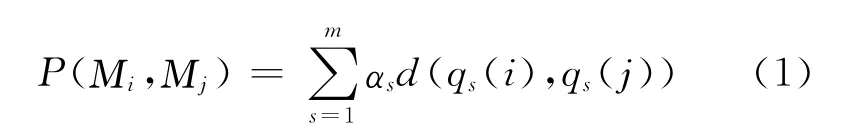
其中，αs（s＝1，2，…，m）为相应关节的加权系数，

（3）帧间距D（Μi，Μj）定义为窗口内各个对应姿态距离的加权之和，即

其中，ωk为窗口中各帧的权重值显然位于窗口中心处的帧权重大于边缘处的帧权重。

任意2帧的间距得到之后，就可构造时间扭曲曲线，将运动序列对齐。

2.2 构造时间扭曲曲线

假设待融合的运动序列为M1、M2，其采样频率相同，帧数分别为n1、n2，组成一个n1×n2的栅格矩阵，单元格（i，j）表示帧对（Μ1（i），Μ2（j））。对运动序列使用DTW算法，以帧间距为度量标准，在栅格矩阵中寻找出一条优化路径，使得路径中所有对应帧的间距之和最小。最简单的做法是将其中一个运动中的一帧与另外一个运动序列中的每一帧计算帧间距，然后组合找出最优解。这种方法可以找到一个全局最优路径，但是时间复杂度高。根据运动序列具有的特征，采用一种较为快速的路径搜索方案，同时可以保证得到的路径较为优化。

为此，定义在路径搜索中需遵循3条规则：

（1）连续性。路径上的每个单元格必须与其相邻的单元格共点或共边。一条不满足连续性的路径如图1a所示。

（2）非递减性。为了保证路径搜索能够结束，规定路径必须始终保持向右或向上延伸。一条不满足非递减性的路径如图1b所示。

（3）倾斜度限制。在水平或者垂直方向上最多只能连续有L个单元格。一条不满足倾斜度限制（L＝3）的路径如图1c所示。

图1 路径规则示意图

为了保证2个运动序列的所有帧均能被时间扭曲，规定路径的起始点B为栅格矩阵的左下角单元格，终止点E为栅格矩阵的右上角单元格。设D（i，j）表示单元格（i，j）对应的帧间距，且D（i，j）≥0，v（i，j）表示从起始点B到（i，j）的距离。显然，只要D（i，j）＞0，在栅格路径中，先水平向右，然后再垂直向上（或先垂直向上，然后水平向右）的代价比倾斜向上的路径代价要大（最好的情况是两者代价相等）。所以，在路径搜索过程中，做如图2所示的路径优化，进一步缩小了路径搜索的范围。为了满足以上定义的3条规则，单元格（i，j）的下一个可能位置最多有2L－1个。当L＝4时，下一个可选单元格的位置分布情况如图3所示。因此，可得出v（i，j）的计算公式为：

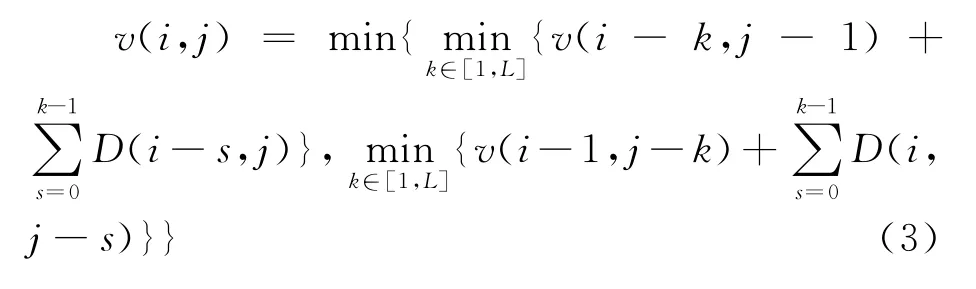
图2 路径优化示意图

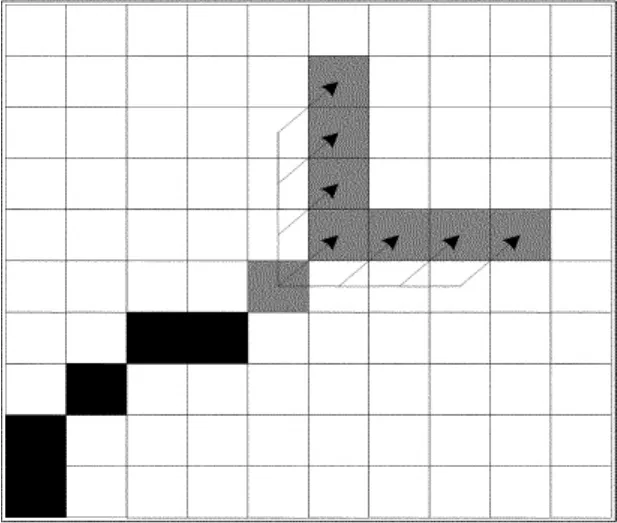
图3 下一个可选单元格

从起始点B开始，根据（3）式计算v（i，j），一直搜索到终止点E，即可构造一条时间扭曲曲线C（v）。

3 运动合成

通过时间扭曲曲线建立了运动序列之间的帧对应关系，依次将对应帧的姿态进行融合、插值，即可得到融合的运动。以帧数较大的运动序列作为模板运动，另一运动序列通过时间扭曲曲线与模板运动对应。所以，融合后运动序列的帧数与模板运动的帧数一致。

即使找到了运动序列的相似帧，对于线性融合也可能会失败。例如，2个行走运动的融合，其中一个运动是向左走动，另一个是向右走动，本来希望融合后的运动是向前行走，但通常的姿态融合方法会使得路径坍塌，造成运动不连续。之所以会造成运动路径的坍塌，是因为对于通常的旋转角度插值方法（如球面线性插值），当旋转角度变化大于180°时会出现插值不连续。为了解决这一问题，本文使用一种简便可行的方法，将运动的局部姿态与运动路径（即角色根关节运动轨迹）分离，然后分别进行融合，最后再通过后处理将其合成完整的角色运动。

3.1 局部姿态融合

忽略角色根关节的运动轨迹，局部姿态完全可用四元数集合表示。因此，局部姿态融合转化为四元数的插值。经典的四元数插值为球面线性插值，主要是在对四元数各个分量分别插值，然后重新规则化使其满足约束条件i2＝j2＝k2＝－1。但是，重新规则化会造成扭曲和单一化的副作用，从而影响动画品质。为了避免重新规则化，本文采用基于指数对数映射的四元数混合方法［14］。在四元数混合中，引入参考四元数q＊，定义为距离q1、q2最近的四元数，它又被称之为四元数均值。通过对数映射将q转换成线性向量v，若说明q＊与q不在同一半球面上，可令q＝－q。通过指数映射q＝q＊ev再将v转换为相应的四元数。依次对两运动序列相似帧中的每个关节旋转数据进行四元数混合，合成连续的局部运动姿态。

3.2 重构根关节运动轨迹

局部姿态融合过程中，没有考虑角色运动路径，忽略了根关节的位移，所以角色只是在原地运动。为了使角色随着姿态的变化而不断改变位置，需重构角色根关节运动轨迹。本文采用文献［14］提出的方法求解插值后的根关节位置。

4 实验结果与分析

以120帧的恐龙行走与100帧的恐龙跑步为例，如图4a所示，将它们进行运动融合。首先，计算2运动序列的帧间距，设定倾斜度限制L＝5，构造一条时间扭曲曲线，如图5所示，采用灰度图表示运动序列的帧间距，颜色越暗其间距越小，反之就越大。融合运动序列中的若干帧姿态如图6所示。

图4 恐龙的2个运动序列

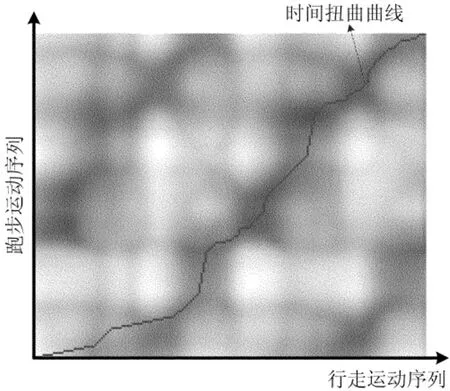
图5 帧间距的灰度图表示及时间扭曲曲线

图6 融合运动序列中的若干帧姿态

5 结束语

本文提出了一种基于时间扭曲图快速搜索的运动融合方法，实现角色不同运动序列之间的融合，通过局部搜索和约束制约计算运动序列帧间距，构造时间扭曲曲线，并对对应姿态进行局部融合，重构角色根关节运动轨迹，合成角色最终的运动。本文提出的运动融合方法，适用于频率不同的角色运动，融合生成的运动效果较好，满足一定的视觉要求。但是在运动融合过程中难免会出现失真现象，所以，在融合过程中加入适当的约束条件以避免运动失真是进一步的研究重点。

［1］王 鑫，孙守迁，柴春雷.3维人体运动编辑与合成技术综述［J］.中国图象图形学报，2009，14（2）：233－242.

［2］卢涤非，任文华，李国军，等.基于样例的交互式三维动画的生成［J］.计算机研究与发展，2010，47（1）：62－71.

［3］Magnenat N，Laperrière R，Thalmann D.Jointdependent local deformations for hand animation and object grasping［C］／／Proceedings on Graphics Interface’88，Edmonton，Alberta，Canada，1988：26－33.

［4］Sturman D J.A brief history of motion capture for computer character animation［C］／／Character Motion System，SIGGRAPH 94：Course 9.

［5］郑利平，王玉培，李 琳，等.基于运动峰值的动画角色肢体运动混合算法［C］／／计算机辅助设计与图形学学术会议（CADCG2010），2010：302－311.

［6］PolichroniadisT，Dodgson N.Motion blending using a classifier system［C］／／Proceedings of the 7th International Conference in Central Europe on Computer Graphics，Visualization and Interactive Digital Media’99（WSCE＇99），University of West Bohemia，Plzen，Czech Republic，1999：225－232.

［7］Unuma M，Anjyo K，Takeuchi R.Fourier principles for e－motion－based human figure animation［C］／／Proceedings of ACM SIGGRAPH 95，1995：91－96.

［8］Rose C，Guenter B，Bodenheimer B，et al.Efficient generation of motion transition using space time constrains［C］／／Proceedings of ACM SIGGRAPH 96，1996：147－154.

［9］Bruderlin A，Williams L.Motion signal processing［C］／／Proceedings of ACM SIGGRAPH 95，1995：97－104.

［10］Park S I，Shin H J，Shin S Y.On－line locomotion generation based on motion blending［C］／／Proceedings of ACM SIGGRAPH，2002：105－111.

［11］Kovar L，Gleicher M.Automated extraction and Parameterization of motions in large data sets［C］／／ACM Transaction on Graphics，2004，23（3）：559－568.

［12］朱登明，王兆其.基于动作单元分析的人体动画合成方法研究［J］.计算机研究与发展，2009，46（4）：610－617.

［13］Hecker C，Raabe B，Enslow R W.Real－time motion retargeting to highly varied user－created morphologies ［C］／／Proceedings of ACM SIGGRAPH’08，2008：1－11.

［14］Lau M，Kuffner J.Behavior planning for character animation［C］／／Proceedings of ACM SIGGRAPH／Eurgraphics SIGGRAPH Symposium on Computer Animation，Los Angles，2005：271－280.