雷达仿真系统场景生成模块设计

李承志 李 炜

(电子科技大学 成都 611731)

1 引言

对于雷达仿真系统，无论是对其进行验证测试，还是为了获得所需要的仿真数据，都必须要有与设想场景相对应的数据，对系统进行初始化和对仿真结果比较验证，这样系统才可能运行并获得想要的结果。因此，每个雷达仿真系统就需要场景生成模块为整个系统运行来提供必要的数据。

本文所设计的场景生成模块主要的功能是模拟空中目标的运动模型，包括:高机动目标运动模型，平稳飞行运动模型，典型弹道导弹的运动模型(应用此思路也可以模拟海中和陆地目标的运动模型)。战斗机、攻击机、轰炸机、预警机、反潜机、侦察机、反舰导弹等航空兵器的运动状态进行仿真。可以根据设置的目标类型、运动方式等参数，产生目标的运动轨迹数据和姿态数据，根据工作时间参数，插值产生当前时刻的目标运动状态，为仿真系统的运行提供目标数据。

2 场景生成模块的总体设计

作为雷达仿真系统整体中的一个模块，在搭建时不仅要考虑本模块要完成的功能，而且还要需要考虑与其他模块之间的相互协调。

首先，完成场景数据生成的功能就是生成每一个目标的轨迹数据，根据所设想的场景，选择目标类型、运动方式、起始的运动状态等参数，初始化目标的状态，然后建立目标运动的六自由度微分方程组，分别描述目标的运动轨迹信息和姿态信息。然后利用龙格库塔法对微分方程组进行求解，将得到的数值解保存到数据文件中。

图1 雷达仿真系统场景生成模块的运行流程图

3 飞行器运动方程组的建立

对于生成场景数据也就是目标轨迹数据生成来说，最重要的算法就是飞行器运动方程组的建立。

飞行运动方程组是描述飞行器的力、力矩与飞行器运动参数(如加速度、速度、位置、姿态等)之间关系的方程组，它是由动力学方程、运动学方程、质量变化方程、几何关系方程和控制关系方程等组成。

3.1 动力学方程

飞行器在空间的运动一般看成可控制的变质量系统具有6个自由度的运动。根据“固化原理”，把变质量系的飞行器当作常质量系来看待，并建立了飞行器动力学基本方程，为研究飞行器运动特性方便起见，通常将这两个矢量方程投影到相应的坐标系上，写成飞行器质心运动的3个动力学标量方程和飞行器绕质心转动的3个动力学标量方程。

a.质心运动的动力学方程

在发射坐标系上建立方程如下:

式中，dv/dt飞行器质心加速度沿切向的投影，称切向加速度;

1.1 一般资料 我院有内科、外科和门急诊等22个临床科室，开放床位628张，护理人员441名。职称:副主任护师4名，主管护师84名，护师177名，护士176名;学历:本科48名，大专219名，中专174名。

V(dv/dt)飞行器质心加速度在铅垂面内沿发射面法线上投影，称为法向加速度;

b.绕质心转动的动力学方程

将飞行器绕质心转动的动力学矢量投影到机体坐标系上最为简单，具体方程如下:

式中，Jx、Jy、Jz分别为飞行器相对于机体坐标系各轴的转动惯量;

ωx、ωy、ωz机体坐标系相对发射坐标系的转动角速度在机体坐标系各轴上的分量;

dωx/dt、dωy/dt、dωz/dt分别表示为机体转动角加速度矢量在机体坐标系各轴上的分量;

Mx、My、Mz分别为作用在飞行器上的所有外力对质心的力矩在机体坐标系各轴上的分量。

3.2 运动学方程

飞行器运动方程组还包括描述各运动参数之间的关系的运动学方程，它将分别建立描述飞行器质心相对发射坐标系运动的运动学方程和飞行器机体相对发射坐标系姿态变化的运动学方程。

a.质心运动的运动学方程

要确定飞行器质心相对于发射坐标系的运动轨迹，需要建立飞行器质心相对于发射坐标系运动的运动学方程:

b.绕质心转动的运动学方程

要确定飞行器在空间的姿态，就需要建立描述飞行器机体相对发射坐标系姿态变化的运动学方程。

3.3 质量变化方程

飞行器在飞行过程中，由于发动机不断地消耗燃料，飞行器质量不断减小。所以，在建立飞行器运动方程组中，还需要补充描述飞行器质量变化的方程，即

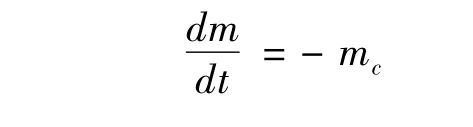
内质量消耗量。

3.4 几何关系方程

联立以上的方程式，在给定初始条件后，用数值积分法就可以解出飞行器的飞行状态和相应的参数变化规律。

4 飞行器运动方程组的数值解法

在得到了飞行器的运动方程组后，另一个重要的算法就是利用数值解法获得方程组的解。

描述飞行器在空间的运动方程组中，在一般情况下，方程右边是运动参数的非线性函数，因此，飞行器运动方程组是非线性的一阶常微分方程组。这样一组方程，通常得不到解析解，只有在一些特殊的情况下，通过大量简化，方能求出近似方程的解析解。但是，在飞行器的轨迹研究中，进行比较精确的计算时，往往不允许进行过分的简化。因此，工程上多运用数值积分方法求解这一微分方程组。数值积分的特点在于可以获得飞行器各运动参数的变化规律，但它只可能获得相应于某些初始条件下的特解，而得不到包含任意常数的一般解。在数值积分时，选取适当的步长、逐步积分计算，计算量一般是很大的。目前广泛采用数字计算机来解算飞行器的飞行轨迹问题，数字计算机能在一定的精度范围内获得微分方程的数值解。计算工作量很大的一条轨迹在数字计算机上很快就能算出结果，这为飞行轨迹的分析研究工作提供了十分便利的条件。

采用数值积分法，常用的方法基本上有三类，即单步法、多步法和预测校正法。这些方法在数值分析教程中都有详细介绍。在数字计算机上常用的微分方程的数值解法有欧拉法、龙格库塔法和阿当姆斯法，本模块采用是龙格库塔法的计算式。

a.龙格库塔法

欧拉法的特点是简单易行，但精度低。在同样计算步长的条件下，龙格库塔法的计算精度要比欧拉法高，但计算工作量要比欧拉法大，其计算方法如下:

设有一阶微分方程:

若已知tk时刻的参数值xk，则可用龙格库塔法求tk+1=tk+Δt时刻的xk+1的近似值。四阶龙格。

b.库塔公式

四阶龙格库塔法每积分一个步长，需要计算四次右端函数值，并将其线性组合求出被积函数的增量Δxk。四阶龙格库塔法除了计算精度较高外，还易于编制计算程序，改变步长方便，也是一种自启动的单步数值积分方法。

5 仿真结果

根据不同的目标和场景设定，对参数进行初始化。然后经过本模块的运行后得到数据文件。将此文件进行仿真验证。

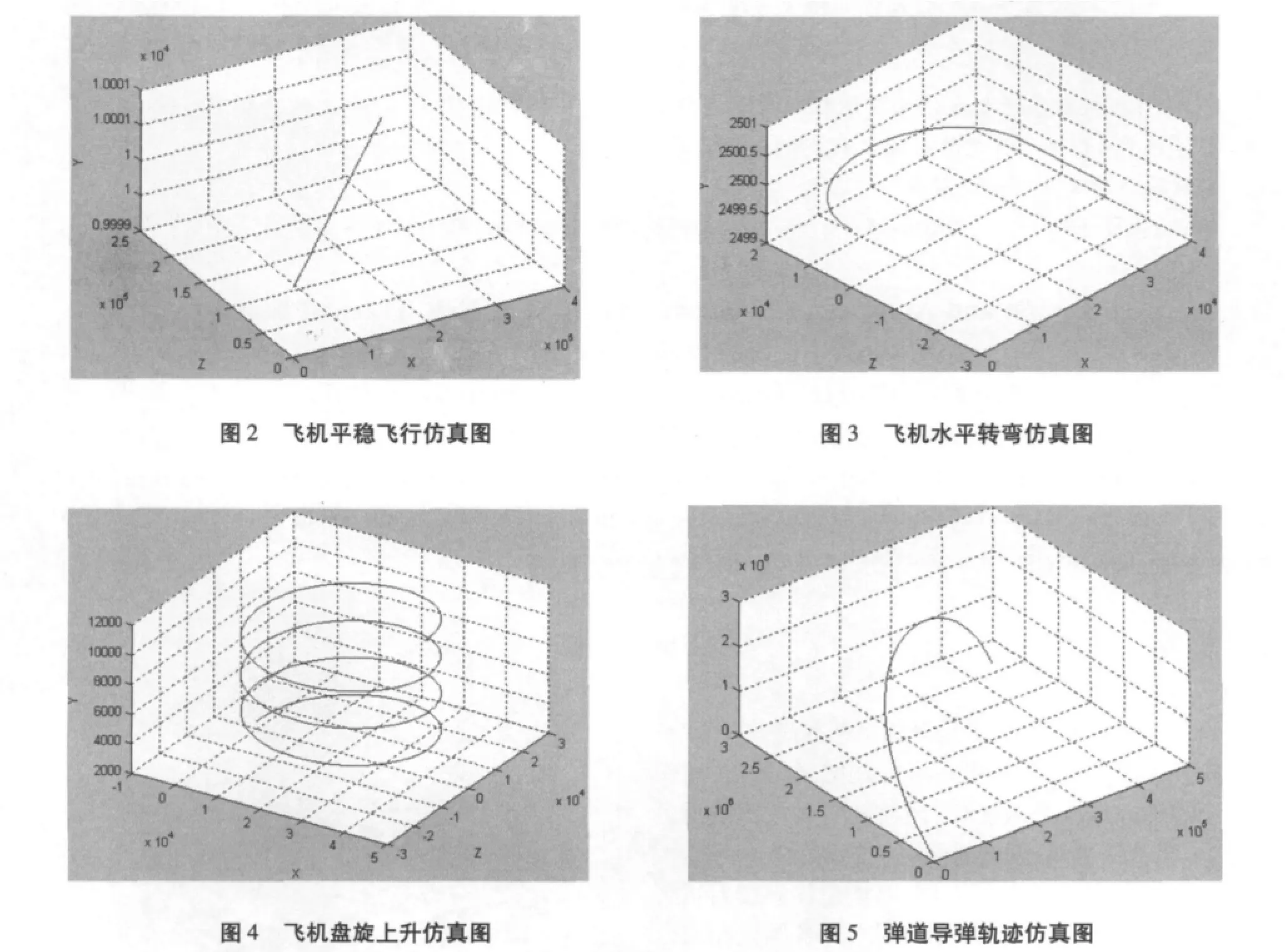
5.1 飞机平稳飞行

平稳飞行即飞机的速度和轨迹偏角不变，以恒定的高度做直线运动。将参数初始化为速度300m/s，轨迹偏角0.67，高度10000m。

5.2 飞机水平转弯

水平转弯是飞行高度不变，速度大小不变的情况下，飞机按照某半径大小作左(右)转弯。初始化参数为速度400m/s，轨迹偏角1.57，高度2500m。

5.3 飞机盘旋上升

盘旋上升为速度不变的情况下，飞机按某半径大小作左(右)转弯，并且以一定速度向上飞行。初始化参数为速度400m/s，轨迹偏角1.57，轨迹倾角0.02.

5.4 弹道导弹轨迹仿真结果

将弹道导弹参数初始化为速度为3000m/s，轨迹倾角0.58，质量为25120kg，程序仿真图见图5。

6 总结

雷达仿真系统的场景生成模块采用本文所设计的思路，可以很好的完成所要实现的功能，即完成目标轨迹数据的生成。经过上述的仿真已经得以验证。同时采用插值的方法也可以与系统的其他模块实时的进行协同运行。下一步需要完善的是提供更多种目标的机动飞行的模式，同时也要提高用户在进行初始化时的方便性。

[1]钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京:北京理工大学出版社.

[2]徐明友，丁松滨.飞行动力学[M].北京:科学出版社.

[3]何旭初，苏煌城，包雪松.计算数学简明教程[M].北京:人民教育出版社.

[4]李荣华，冯果忱.微分方程数值解法[M].北京:人民教育出版社.