差分GPS应用于机载雷达精度统计的方法研究

牟聪王伟张明

(西安电子工研究所 西安 710100)

1 引言

雷达精度是衡量雷达战术性能的的重要指标，目前在国内外的精度评估研究中，很多是使用仿真数据来进行的，与实际情况存在较大差异，也有采用目标模拟器验证受试雷达的距离、方位、速度等相关数据精度，但是由于对于机载雷达数据的处理，涉及到机载惯导的补偿精度、伺服系统的精准度等，因此这种方法存在极大的局限性，而且准确度和实际使用结合很不紧密。本文介绍一种基于差分GPS的机载雷达精度统计分析方法，相对于传统的方法，具有涉及的设备数量少，人员投入少、准备时间短的优点，并且已经成功地应用于某机载雷达的定型挂飞试验，保障了项目的成功定型。

2 相关理论

差分GPS上报的是基于WGS－84坐标系的球坐标数据，即经度、纬度、高度，除此之外，GPS通常还上报东速、北速、天速等数据，可用于目标的速度精度评估。地面上某一点的经度为过该点的椭球子午面与格林威治起始子午面的夹角，大地纬度为过该点的椭球法线与椭球赤道面的夹角，高度为该点沿椭球面法线至椭球面的距离，机载雷达通常为了导弹或者炮弹制导的要求，所上报的目标坐标数据都是基于载机坐标系，为了验证雷达上报目标数据精度，可以用高精度的GPS作为基准真值，与雷达的数据进行匹配，来计算雷达的精度，要完成上述的功能，需完成如图1所示的坐标转换。?

图1 坐标转换顺序框图

2.1 相关坐标系的定义

a.GPS 坐标系[1]

GPS最常用的坐标系是WGS-84坐标。

WGS-84是一个协议地球参考系CTS。该坐标系的原点是地球的质心，Z轴指向 BIH1984.0定义的协议地球极 CTP(Conventional Terrestrial Pole)，X轴指向BIH1984.0零度子午面和CTP赤道的交点，Y轴和Z、X轴构成右手坐标系。

b.载机坐标系[2]

载机坐标系原点定义为载机的质心或者几何中心，X轴以载机纵轴机头为正向，Y轴定义为右翼正向，Z轴通过右手螺旋定则确定指向机体下方。

c.载机地理坐标系[2]

载机地理坐标系的原点是载机的质心或者几何中心，也就是说和载机坐标系是同心的，X轴指向载机所在地理位置的正北方N，Y轴指向载机所在地理位置的正东方E，Z轴与X，Y轴构成右手坐标系，指向机体下方，又称为NED坐标系。

2.2 相关的的坐标转换方法

a.GPS坐标系到WGS-84坐标系的转换[2]

假定目标 GPS 坐标为(Bt，Lt，Ht)，其对应的WGS-84 坐标系直角坐标为(Xt，Yt，Zt)

从(1)式同样可以得到载机所在的WGS-84坐标系的坐标，记为(Xr，Yr，Zr)，其中假定雷达载机的GPS 坐标为(Br，Lr，Hr)。

b.WGS-84坐标系到载机地理坐标系的转换[3]为了得到目标在载机地理坐标系中的坐标数据，必须通过如下两步坐标转换:坐标平移、坐标旋转。这里所谓坐标平移就是将目标的WGS-84大地坐标系数据平移至以雷达载机地理坐标系的原点为原点，其三轴分别平行于WGS-84大地坐标系的坐标系，转换过程如下式:

则目标位于载机地理坐标系的目标坐标(Xrt，Yrt，Zrt)为:

c.载机地理坐标系到载机坐标系的转换

一般的机载雷达目标数据的观测总是基于载机坐标系，我们假设当前载机的姿态角为(α，β，γ)，其中α为载机的横滚角，β为目标的纵摇角，γ为目标的偏航角，则对应的变换矩阵我们记为C，我们可以称C为姿态矩阵，C的表达式如下[1]:

则使用上式中的姿态矩阵C，可以得到转换到载机坐标系中的目标坐标(X，Y，Z):

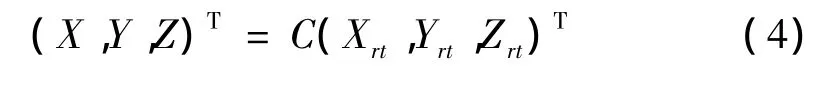
d.载机坐标系直角坐标向极坐标的转换

由于雷达的观测所提供的数据是基于载机坐标系的极坐标数据，因此我们得到上述的载机坐标系的直角坐标数据后还需要将其转换到相应的极坐标形式，转换公式如下:

式中，R为目标的距离，θ为目标的方位角，φ为目标的俯仰角。

2.3 径向速度的计算

假设目标的GPS上报的速度向量为(Vte，Vtn，Vtu)，其中 Vte为东速，Vtn为北速，Vtu为天速，载机GPS上报的速度向量为(Vre，Vrn，Vru)，各个分量的定义与目标GPS的向量定义相同。为了计算径向速度的大小，需要计算出速度两者的速度差:

根据(3)式的结果，对于目标相对于雷达的径向速度计算:

2.4 数据的时间对齐

对于机载雷达的应用实际，尤其在对空试飞中，目标和雷达载机相对飞行时，对于目前GPS较常采用采样频率20Hz和50Hz来说，每一次的采样间隔之间，目标和载机的相对距离变化都会达到数米，因此会引入较大的误差，如果要准确的得到目标观测数据的误差，需要将GPS数据按照时间外推到雷达所观测目标的时刻上，这样才能做出更加客观和准确的对比。在实际中，我们可以假设雷达对目标的观测时间为t，GPS的采样间隔为T，假设GPS第nT和第(n+1)T个时刻雷达有观测值，且nT＜t＜(n+1)T，则不失一般性，假设GPS在nT时刻的采样值为χn，在(n+1)T时刻的采样值为χn+1，在t时刻的值χt:

通过上式，就可以将GPS的观测信息外推到雷达的观测时刻t上，完成时间的对齐，通常对于机载雷达来说，载机的速度通常不会在1/20s或者1/50s发生明显变化，较地面雷达来说，机动比较平缓，因此上述的(8)式可以达到相当高的外推准确度。

2.5 数据的统计

GJB2137-8-94对统计数据计算方法规定如下[4]:

a.系统误差的统计

系统误差按照测量误差值的数学期望进行统计，计算公式为:

b.随机误差的统计

随机误差按照测量值的均方差进行统计:

（四）通过内部控制推动指标动态优化，实现指标设定与单位事权相一致。在评价过程中，各单位要将预算绩效的通用指标根据自身特点进行调整，制定出一套科学、合理、持续优化的绩效评价指标体系。绩效评价指标的建立要充分考虑到本单位的预算效益，同时要提高对评价指标设定的重视程度，形成具有本单位特色的绩效评价指标体系。从更广的角度看，还应注意指标信息积累，收集不同单位和部门的绩效评价指标，进一步补充完善评价指标体系，建立一整套覆盖范围广、适用性强的指标体系，可建立指标库。

在上述的(9)、(10)式中:M(X)为系统误差分量，σ为随机误差分量，n为有效实验次数，mi为第i次试验数据采样点数，Xij为第i次试验中第j个采样时刻的雷达目标坐标值。

c.数据精度是否满足的判决

当系统误差和随机误差符合相关的机载雷达战术技术指标要求时，则认为精度满足要求，否则，则认为不满足。对于机载雷达来说，在精度挂飞前，一般已经进行了地面静态校靶和飞行状态动态校靶，所以可以认为系统误差已经消除，只要随机误差满足要求即可。

3 应用实例

在应用实例中，在载机和目标机上各加装一台差分GPS接收机，采用的是NovAtel高精度存储型差分GPS接收机，型号为DL-V3，它具有如下几方面和精度评估相关的指标:

测量目标距离:≤50km;连续使用时间:≤6h;定位数据更新率:50Hz;时间精度:20ns;速度精度:0.03m/s;速度限制:≤515m/s

运动测量精度:

基线长:0～15km 定位精度:≤20cm

基线长度:15～50km 定位精度:≤50cm

3.1 适用性分析

根据误差传递函数:即设函数y=f(x1，x2，…，xn)，其中x1，x2…xn为具有均方根误差 σx1，σx2…σxn的独立的变量，函数y=f(x1，x2，…，xn)具有对每一个变量的连续偏导数，则:

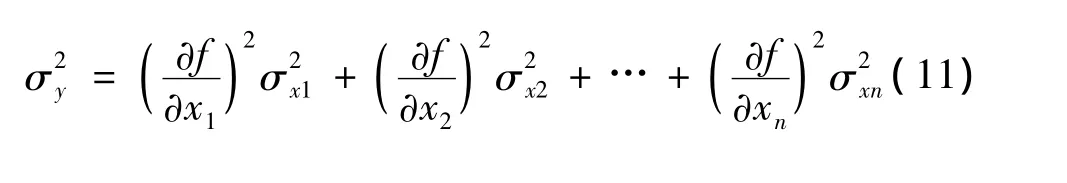
对于本应用，假设雷达载机的GPS大地坐标系坐标为(x1，y1，z1)，目标的 GPS 大地坐标为(x1，y2，z2)，则距离应该为:

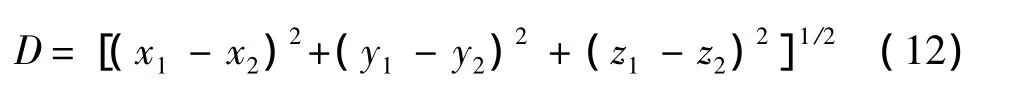
对x1－x2分量，其最大的精度误差根据(10)式和GPS的参数，令x=x1－x2。可得:

同理，令 y=y1－ y2，z=z1－ z2，有如下式成立:

对于(11)式可简化如下:

由式(10)可得由于GPS的精度误差导致的距离精度误差为:由于GPS的定位精度最大不超过50cm，因此即使两者的误差在方位向上叠加，对方位向上在1km时对方位的影响不超过0.1°。

同理，可以证明由于GPS的测速误差导致的径向速度精度误差远远小于1m/s。

对于机载雷达的精度要求一般要求距离精度小于10m，方位精度小于0.5°，速度精度小于10m/s，而对设备的使用一般要求标准测量设备的精度小于被测精度的1/3，所选差分GPS显然能很好的满足应用的要求。

3.2 试飞应用

在试飞数据的处理时，由于一般对于不同操作系统对文件大小的限制和不同的模式需要存储在不同的文件中，因此，一次挂飞的数据存储在若干个数据文件中。在实际的使用中，应先对文件进行时间上的排序，并对不同距离段、不同参数情况分别统计精度结果，具体步骤如下:

a.文件初始化

主要完成数据处理的目标数据文件按时间排序，并将每一个文件或者文件不同的数据帧所对应的雷达操作控制参数进行标记。

b.目标匹配

由于数据处理所存储的目标数据，既有合作目标的，也有大量非合作目标的，因此要做精度统计，必须将合作目标的航迹提取出来，对每一个数据文件，按顺序将所有目标数据逐次和同一时刻的目标GPS、载机GPS按(1)式～(7)式计算出的数据做匹配，可以预先设置门限，当距离、方位、速度、俯仰差值小于预置门限时，则认为是匹配上的，即数据处理的某一目标数据为合作目标，否则，则不是。

对于匹配上的目标，有可能某一时刻有两个目标都和真实的GPS都匹配上，这时候则要根据运动趋势规律将和真实目标GPS变化规律不一样的剔除，只有航迹存在时间段运动规律和GPS变化规律相同的才能认为是合作目标。

c.精度统计

以匹配上的目标数据点作为观测点，将匹配上的GPS位置外推到目标所在的时刻，作为真值，按照(9)、(10)式进行精度统计并判定。

使用如上方法已经成功的开发出了相应的软件，软件主界面如图2所示。

图2 精度统计软件主界面

4 结论

上述所构建的方法通过在某型雷达定型挂飞中的实际应用，成功的保证了雷达的成功定型，也验证了其方法的可行性和正确性。由于其在精度计算时，根据(9)要计算系统误差，因此，其也可以应用于机载雷达的动态校靶，具有良好的可推广性。

[1]李征航，黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社，2005.

[2]常军.机载雷达目标的大地坐标定位[J].电讯技术，2003，(2):97 ～100.

[3]田伟.雷达精度实验中GPS数据坐标转换及误差分析[J].雷达与对抗，2007，(2):54～56.

[4]曹桂兰等.GJB 2137-8-94.机载雷达通用要求-飞行验证要求[S].中华人民共和国国家军用标准.