机械功率对电力系统稳定性的影响
邵明珠 罗诗裕
(东莞理工学院 电子工程学院,广东东莞 523808)
机械功率对电力系统稳定性的影响
邵明珠 罗诗裕
(东莞理工学院 电子工程学院,广东东莞 523808)
从摆方程出发,借助能量法和相平面分析方法对电力系统的稳定性进行讨论。结果表明,当机械功率比较小的时候,系统的稳定性不受影响;当机械功率比较大时系统的不稳定性开始凸现,机械功率越大系统越不稳定。当机械功率等于电磁功率时,系统处于临界状态。系统的临界状态与系统参数有关,只需适当调节这些参数就可以保证系统是稳定的。
电力系统;稳定性;摆方程;能量法;相平面分析法
电力系统是一个典型的动力学系统,它的动态行为包含了复杂的非线性。电力系统的混沌振荡、频率崩溃和电压崩溃是导致电网事故的三大主要原因。1966年,美国西北、西南两大电网互联后不久,就曾发生过1分钟内出现6次“从未见过的”振荡现象,导致两系统解列。1996年,我国华北电网也曾发生过1分44秒内的严重振荡现象,导致入京电网与地方电网解列,造成了严重的“5.28”华北电网事故。可见,电力系统的稳定性问题是工程和技术十分关注的问题。
系统动力学理论指出,对于弱周期扰动情形,可建立二维Poincare映射。如果一个平面映射存在Smale马蹄,这个映射就具有反映混沌属性的不变集,系统就会出现Smale马蹄变换意义下的混沌行为,而Melnikov方法则是判定这类系统是否具有Smale马蹄变换的一种解析方法。如果系统还存在一族周期轨道,则Melnikov方法还可以用来判断次谐分叉轨道是否存在及其轨道的稳定性。文献 [1-5]就用Melnikov方法分析了系统的分叉与Smale马蹄混沌行为。
电磁功率对系统稳定性影响问题是一个值得关注的问题,以前的工作大都是将它作为系统参数之一进行讨论。这种分析的特点是从全局出发对系统的稳定性进行分析。换句话说,这种分析是将系统参数做为“整体”(集合),并从系统稳定性出发,对这些参数的相对大小进行估计。本文企图从局部出发,把机械功率从参数集合中抽出来单独进行分析,特别是对系统稳定性的影响进行分析。也许,只有当人们从“整体”和“个别”出发对系统的稳定性进行分析后才可能对动力学系统有一个全面认识。
基于简单互联的电力系统模型,人们已把电力系统运行的工程技术问题转化为具有阻尼项、受迫项和固定力矩的“摆动”问题。在本文中,我们暂不考虑系统的阻尼项和受迫项,只讨论机械功率对系统稳定运行的影响。这时,描述系统的动力学方程退化为具有外力矩的摆方程,机械功率对电力系统的影响就等效于外力矩对摆动影响。本文就从这个具有外力矩的摆方程出发,借助能量法和相平面分析方法对电力系统的稳定性进行讨论。结果表明,当机械功率比较小的时候,系统的基本特征由无扰动系统决定,小的机械功率只导致相平面特征的微小变化,系统的稳定性不受影响;当机械功率比较大时系统的不稳定性开始凸现,机械功率越大系统越不稳定。当机械功率等于电磁功率时,系统处于临界状态。系统的临界状态与系统参数有关,只需适当调节这些参数就可以保证系统是稳定的。
1 运动方程
涉及电力系统的一个重要问题就是它的物理模型问题。人们在不同的近似下提出了不同的物理模型对它进行了描述,其中简单互联的电力系统模型是一个用得最多、最广泛的物理模型。从这个模型出
发,可导出相角ξ满足的动力学方程

其中

而

Pm是发电机的机械功率,Ps是发电机的电磁功率,H是发电机等效转动惯量,δ0是平衡相位。其他参数的意义见文献 [6-7]。如果不考虑系统的阻尼项和受迫项影响,方程 (1)可化为

系统 (4)的Hamiltonian由公式 (5)给出
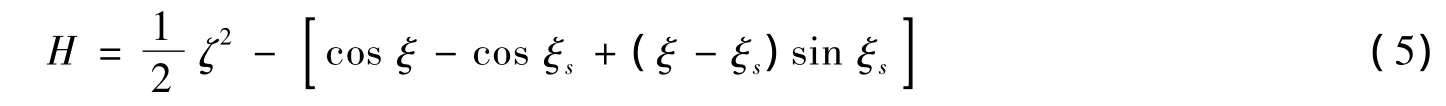
其中ξs=arcsin σ。下面分别对σ=0和σ≠0两种情况进行讨论。
2 无扰动系统的相平面特征
对于无扰动 (σ=0)系统,方程 (4)化为

或等价系统

系统 (7)有一个稳定固定点(ξ,ζ)SEP=(0,0)和两个不稳定固定点(ξ,ζ)UFP=(±π,0),且存在如下形式的运动积分

根据h的大小,相平面上的轨道可分为三类。
1)h=2。h=2的轨道是异宿轨道,且可将它表示为

其中±号分别对应上、下相平面的两条异宿轨道,这两条轨道把相平面分为内外两个区域。系统沿这条轨道运动的周期Ts为无穷。
2)0<h<2。当0<h<2时,轨道是周期的,描写的是系统围绕平衡位置的周期运动,相应的解可表示为

其中k=h/2是椭园函数的模,k∈(0,1),snτ和cnτ是Jacobian椭园函数。系统沿这条轨道的运动周期
K(κ)是第一类椭园积分。当h单调增加时,系统的周期T0从2π增加到无穷。
3)h>2。当h>2时,轨道也是周期的,描写了系统围绕不稳定平衡位置的周期运动,且可用Jacobian椭园函数表示为


式中κ'是椭园函数的补模,dnτ为Jacobian椭园函数。振动周期由

给出,当h单调减少时,周期Tr由零增加到无穷。
3 系统的稳定性
3.1 能量法
如果σ是一个小量,系统的稳定性可以用能量法进行分析。由于σ是一小量,系统的相平面特征与无扰动系统基本一样。考虑到扰动效应,系统的解可近似地表示为

其中O(σ)表示与σ同阶的小量。从物理上考虑,扰动结果相当于外力矩作用使系统能量增加所作的功。而外力矩作功可以表示为

积分上下限表示外力矩作用区域。将式 (9),(10)和 (11)代入上式,完成积分可分别得到

可以看出,由于外力矩作用,系统的能量增加了Wi(i=1,2,3)。于是,系统的能量积分 (8)发生了相应变化,由式 (14),(15),(16)还可具体表示为

比较式 (17)和 (8)可以看出,由于外力矩作用,系统的相平面特征发生了变化。方程 (17)描写的是相柱面上哪类轨道决定于h+W2和h+W3的值。当h+W2<2+W3时,系统仍然是稳定的。
根据刘维定理,对于保守系统,相面积保持不变。由于外力矩的作用,系统的相面积将发生变化。力矩引起的相面积变化可表示为

其中s0是外力矩为零时系统的相面积,s是外力矩不为零时系统的相面积。假设粒子的相空间密度是均匀的,稳定系数可定义为

对于振荡型周期轨道 (10),相面积大小由异宿轨道 (9)包含的相面积决定,且可具体表示为

其中E(κ,φ)和F(κ,φ)分别是第二类和第一类椭圆函数,而

对式 (20)微分,并代入式 (19),可得系统的稳定系数

其中Δh=W2由式 (15)给出。
3.2 相平面分析方法
如果σ不是小量,系统的稳定性可借助相平面分析方法进行讨论。假设相平面上相点的分布是均匀的,系统的稳定性则由相面积决定,面积越大系统越稳定。为此,需首先求出σ=0对性σ≠0情况下系统的相面积。引入作用量

将式 (10)代入,并完成积分,可得
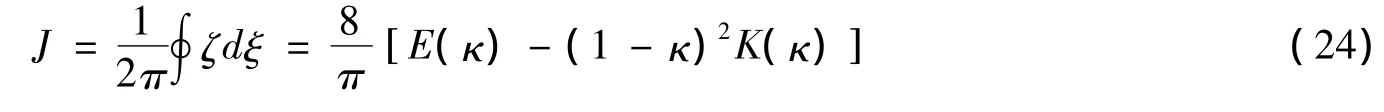


当σ≠0时,系统 (6)有一个稳定固定点(ξ,ζ)SFP=(ξs,0)和一个不稳定固定点(ξ,ζ)UFP=(π-ξs,0)。分支线 (同宿轨道)的Hamiltonian值为

而分支线的相轨迹可表示为H=Hsx或

分支线有两个零点ξu和π-ξs,其中ξu由方程 (28)给出。

图1给出了σ=0;0.2;0.4;0.6;0.8;1等情况下的分支轨道。对应于σ=0的分支轨道是异宿轨道。

图1 从外到内σ=0;0.2;0.4;0.6;0.8;1时系统的相平面特征
对应于σ≠0的分支轨道是同宿轨道。同宿轨道包围的面积 (如图1所示α-形区域)由公式 (29)给出

其中α(ξs)是ξs≠0和ξs=0时分支线包围的面积比α(ξs)=Aα/Ao,并可表示为下列积分
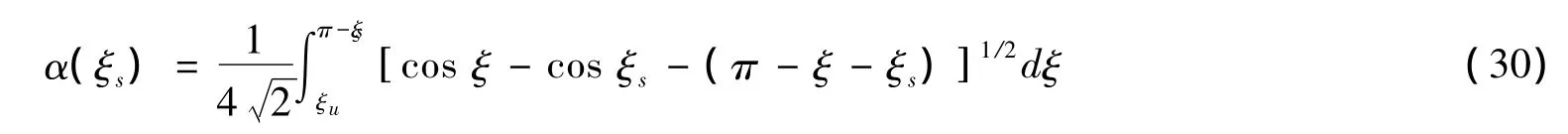
且可近似由公式 (31)给出。

式 (25)和 (29)分别给出了异宿轨道和同宿轨道包围的面积,而系统的稳定性正好由公式 (31)决定。
分析表明,当σ=1时,系统处于临界状态。由式 (2)可知σ=Pm/Ps,临界条件σ=1给出了

上面的分析表明,当机械功率比较大时系统的不稳定性开始凸现,机械功率越大系统越不稳定。当机械功率等于电磁功率时,系统处于临界状态。
4 结论
机械功率对系统稳定性影响问题是一个值得关注的问题,以前的工作大都是将它作为系统参数之一进行讨论,本文把它从参数集合中抽出来单独进行分析。描述电力系统的动力学方程是一个包含了阻尼项、受迫项和固定力矩的广义摆方程。本文讨论了机械功率 (固定力矩)对系统稳定运行的影响。描述系统的动力学方程是一个为具有外力矩的摆方程,机械功率对电力系统的影响就等效于外力矩对摆动系统的影响。利用能量法和相平面分析方法对电力系统的稳定性进行了讨论。结果表明,当机械功率比较小的时候,系统的基本特征由无扰动系统决定,小的机械功率只导致相平面特征的微小变化,系统的稳定性不受影响;当机械功率比较大时系统的不稳定性开始凸现,机械功率越大系统越不稳定。当机械功率等于电磁功率时,系统处于临界状态。系统的临界状态与系统参数有关,只需适当调节这些参数就可以保证系统是稳定的。
[1]王宝华,杨成梧,张强.电力系统分叉与混沌研究综述[J].电工技术学报,2005,20(7):1-10.
[2]张强.电力系统非线性振荡研究[J].电力自动化设备,2002,22(5):17-19.
[3]罗晓华.简单互联电力系统的相平面特征与混沌振荡[J].东莞理工学院学报,2008,15(1):35-37.
[4]张卫东,张伟年.电力系统混沌振荡的参数分析[J].电网技术,2000,24(12):17-20.
[5]罗诗裕,邵明珠,刘曾荣,等.弯晶沟道的混沌行为[J].物理学报,1988,37(8):1394-1399.
[6]邵明珠,罗诗裕.简单互联电力系统的全局分叉与混沌行为[J].东莞理工学院学报,2009,16(5):17-22.
[7]邵明珠,罗诗裕.二阶非线性对简单互联电力系统稳定性的影响[J].东莞理工学院学报,2011,18(1):51-54.
The Impact of Mechanical Power on Power System Stability
SHAO Ming-zhu LUO Shi-yu
(College of Electronic Engineering,Dongguan University of Technology,Dongguan 523808,China)
The paper discussed the stability of power systems by using the energy method and phase plane analysis method from the pendulum equation.The results show that when the mechanical power is relatively small,the stability of the system is not affected;when mechanical power is large,the instability of the system has become distinct,and the larger mechanical power is,the more instability.When mechanical power is equal to the electromagnetic power,the system is in critical condition.The critical condition of the systems is related to system parameters,just adjusting appropriately these parameters so as to ensure stabilities of the system.
power system;stability;pendulum equantion;energy method;analyseis method of phase plane
TM 712;O415.5
A
1009-0312(2012)01-0039-05
2011-04-26
邵明珠 (1942—),女,浙江宁波人,教授,主要从事电粒子与物质相互作用研究。

