暗物质之迷
任海涛
(莆田学院 电子信息工程学系,福建莆田 351100)
暗物质之迷
任海涛
(莆田学院 电子信息工程学系,福建莆田 351100)
由星系团的运行速度观测而推测出来的宇宙中含有大量暗物质的理论似乎获得了大部分物理学界和天文学界的人的认同。而我却不认同此理论,因为事实上并不存大大量的暗物质,只要将整个星系的各个恒星对星系边沿的恒星的万有引力重新逐个计算并统计引力效应就能得到边沿恒星绕行所需要的引力值。使得万有引力的增大的原因在于临边陡增效应和力桥效应,并由此提出了万有引力新的表述。
暗物质;引力;统计;效应
1 并不存在大量的暗物质
事实上并不存在大量的暗物质[1],只要将整个星系的各个恒星对星系边沿的恒星的万有引力重新逐个计算并统计引力效应就能得到边沿恒星绕行所需要的引力值,而目前是先统计出整个星系的质量M后,并结合半径R,以万有引力是等于恒星运行的向心力的公式[2]。推导出提供给边沿恒星所需的向心力的质量远大于观测到的该星系的总质量。于是暗物质的假说被提出来了。其实只要将该星系内各个恒星对所测边沿恒星的万有引力在向心方向的引力效应全部统计出来就能得到与边沿恒星本该有的向心力相当的力。具体的统计是相当复杂的。因此,在此只对一个理想的扁平圆形均匀分布的星系提出一个近似的引力统计公式。
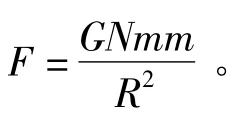
但将这N个均匀分布的恒星分别对边沿星的在向心方向的引力效应计算出来并相加得到的引力效应是不同于GNmm/R2。因为该星系近似均匀分布,所以我将该星系分成imax个圈,分别分1圈,2圈,3圈,…,i圈,…,imax圈。第i个圈上就有2πi个恒星,各个圈之间的距离为r,即各个恒星与相邻的恒星的间距是r。
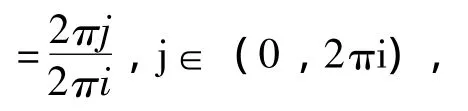
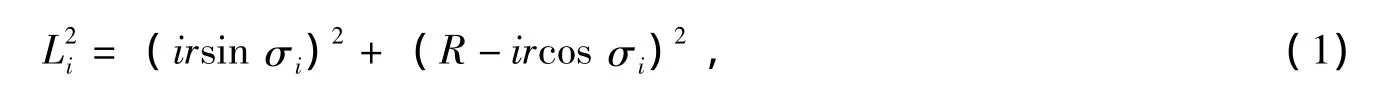
向心力方向的分力

向心方向的力效总和
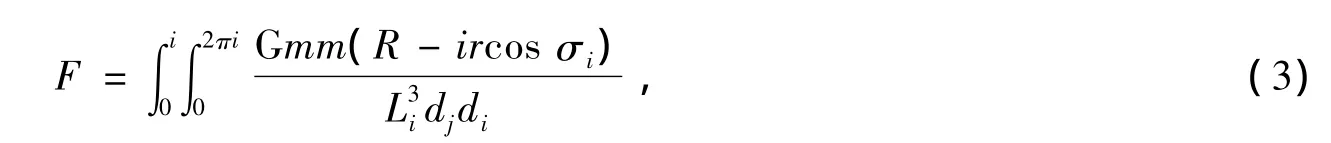
此力效总和必然远大于先统计总质量的方法计算出来的万有引力。其原因是星系盘高被严重压缩。那么它就不能用来表示实际上边沿恒星受到的力效总和,该公式的用处在于可能求得一个常数K的近似值。
宇宙中星系的形状各异,但大多数为椭圆形盘状星系。盘高H都小于半径R,盘高越小统计力效应该越大。所以,实际上的力效公式应为

K可通过设定H为恒星半径并结合事实观测来确定。
2 更符合星系实际的统计方法
由公式 (3)来求极限情况 (盘高为恒星半径)下的力效总和并不符合星系的实际情况,星系中恒星密度是从外向内逐渐变高的,所以将各个i圈的恒星个数都设为一定值Q更符合实际情况,各圈与相邻圈的距离仍为r,那么由N=Q×imax得imax=N/Q。
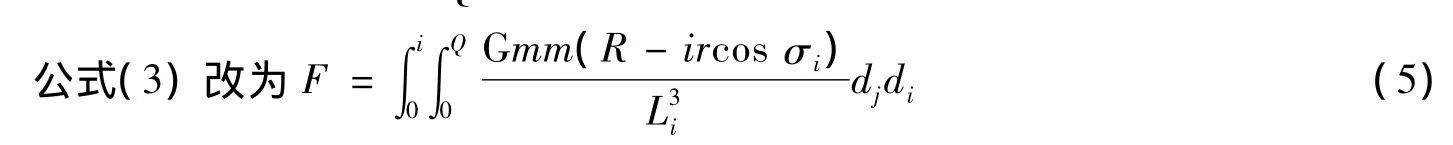
由公式 (5)求极限情况下的力效总和比较符合星系的实际情况,进而得到的K值也较为合理。而星系边沿的恒星实际上的力效能否用公式 (4)来求取,关键在于能否找到一个较为合适的r值。
由两种模拟的星系求得的力效虽然更为接近引力的真实值,但宇宙中星系形态各异,有的与两种模拟形态相差甚远,所以得到的结果与真实值的差距也可能会很大,所以最直接、最有效的办法还是逐一统计,在目前的科学技术下借助于大型计算机和天文望远镜是可以办到的。
3 统计力效的关键在于临边 (近)陡增效应
对于力效的统计不能用盘形的统计方法,即将原本是球状的星系的旋转中心线进行压缩,一段中心线切向上的所有质量集中于中心线。这样的统计是没有什么意义的,因为即使最顶上的那个小盘压缩到赤道,它增加后的引力效果也才原来的两倍。其原因在于此把各小盘的质量集中于中心线是错误的。
统计力效的可实现数倍的增量的关键在于临边 (近)效应,如图1示。
设图中的圆为以星系中心与边沿恒星 (A)的连线为半径的一个子午圆,当子午圆上的恒星 (m)靠近边沿恒星时,它与边沿恒星的距离 (LAB)与垂直压缩后的距离 (LAB’)的比值大增 (超过2)。它们之间的引力将变为原来的值乘以比值的平方,达到一个陡增的效应。将B压缩到B’其实与实际不符,为什么不是压缩到BB’线上的其它点呢?如果将盘高压缩一倍,那么BB’线上的质量就等效于从中点处折断,并垂直落下,B点就落在了原来的BB’中点处,而原来的中点落在了OA线上。这样虽然AB间的引力增效不会太大,但是BB’中点处与A的引力增效还是很大的。当分析CC’时,中点处的引力增效将会更大。所以,其它恒星越靠近边沿恒星时,它们的引力增效将呈现陡增的趋势。这就是统计力效会达到数倍甚至数十倍于先统计总质量的方法计算出来的万有引力。
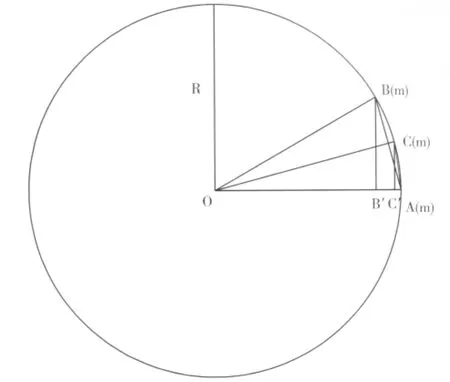
图1 临边效应简析图
4 力桥效应与多余带动效应
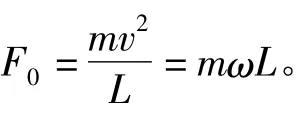
是否铁球1绕O点以速度V做圆周运动,它受力就一定是F0呢?来继续做这个实验,将绳子与测力计1连接的地方连接另一个质量也为m的铁球2,而原来的测力计1换成以L/4长的绳子与L/4长的测力计2并前后相互连接起来,如图2示。

图2 力桥效应例析图
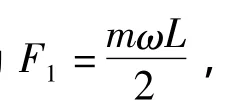
绳子长为L时,可以很自然的认为O点处受力也为F0。但当从中间连上了铁球2时,O点受力是多少呢?一般都会认为受力肯定会增加,然而只要不要想当然而是老老实实的去做受力分析,就会发现O处受力仍然为F0。因为只看铁球2,它距离O为L/2,角速度为W,所以受力大小为F1。而铁球2为了克服铁球1对它施加的拉力F1,它就需要一个与F1大小相等方向相反的力。由此可知,圆心O与铁球2之间受力仍然为F0。
这种在向心力之间连接一个有质量的物体并随着原来的受力系统一起运动且不改变原来系统的相对运动时,圆心处的受力大小不变的效应为多余带动效应。而之所以会认为受力会变大是因为在地球上做这样的实验时,圆心处还要额外的提供一个力来克服铁球2的重力。
如果将这个实验改为太阳系的一个观测性实验。O点为太阳,m2为地球,m1为卫星 (此时m1<<m2),假设卫星不受太阳的作用而围绕地球做周期为一天的圆周运动,并且一直处于黑夜零辰。这在远处 (其它太阳系或恒星系)的观测效果等效于卫星围绕太阳做周期为一年的近似圆周运动,并把它做此圆周运动所需要的向心力主要归于太阳与卫星的万有引力。事实上如果卫星做这样的运动时它相距地球中心约41 900 km,如果太阳光到达地球用时8分钟,那么由公式
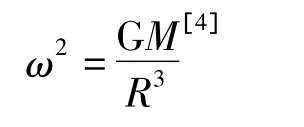
且卫星与地球相对太阳的角速度相等。从而由卫星速度计算出太阳的质量为用地球计算出来的质量的1.000 89倍。事实上并不存在这多余的0.000 89倍太阳质量 (产生了所谓的暗物质),其产生原因在于将卫星看作围绕太阳运动,而地球和太阳一起的质心与单太阳的质心基本在同一点。如果将地球换成另一个质量更大的星体,如恒星2,其质量与太阳一样,其它运行方式和地球一样,距离为日—地距离,而卫星仍像围绕地球一样运动,只是它的半径变为了原来的32倍 (即134万km)。这样由卫星的速度和上面的公式计算出太阳的质量将为原来的1.028倍。但此时的质心变化非常大,不得不考虑。那么可以设想在太阳的另一边放三个等质量的恒星,相互间距也为日—地距离,都围绕质心做周期为一年的圆周运动。由此,卫星到现在的质心的距离约为2.5倍日—地距离,计算出来的质量为15.625倍太阳质量,而事实上只有5个太阳质量。当然,这样的系统是不可能围绕质心做圆周运动的。但是由星系边沿恒星的速度和这种力桥效应计算出来的星系质量完全有可能达到星系实际质量的数倍。
所以统计力效的陡增效应与力桥效应在星系的观测上可以解释为什么边沿恒星绕星系中心的运动速度比经典的牛顿引力得到的要高,即可证明星系内并不存在大量的暗物质。而多余带动效应也可以用来解释不是边沿和中心处的其它恒星的运动。
5 边沿恒星受力的简化公式与万有引力的新表述
从上面的诸多推导可以消除星系中存在大量暗物质的假说,但在实际统计上相当繁琐而不可取,所以有必要将边沿恒星的受力做一个整合与重新估算 (或者说是一个新的表述)。由上面的推导可以写出一个标准压缩成盘的星系中边沿恒星受力的大概的公式:
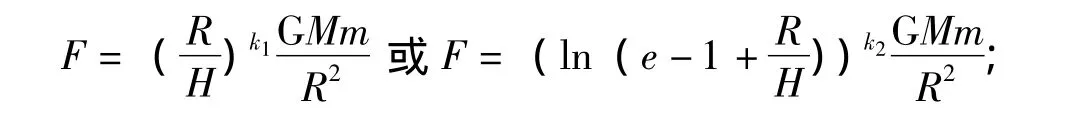
又或
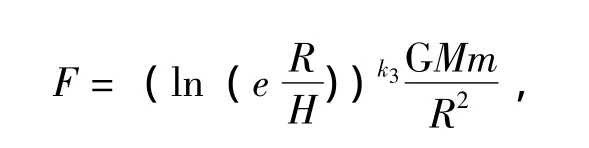
公式的选取取决于实际观测:R为边沿恒星到星系中心的距离;H为星系的盘高;M为星系的总质量;m为边沿恒星的质量;G为万有引力常数[5];k为标准系数 (当星系盘为标准压缩时k取1,而非标准压缩时k取1左右两边的值)。
由上面的边沿恒星的受力公式可以猜想万有引力的表述是否可以用一种更为精确的方式来表述呢?答案是肯定的,否则万有引力如何将边沿恒星的受力情况包含在内呢!
要得到这样一个万有引力公式的新表述必须有两点要求:在特定情况下可用于标准压缩下边沿恒星的受力分析;在一般情况下仍然满足牛顿表述。要满足这两个要求k值在一般情况下接近0,而在特殊情况下大于0(或小于0)。由此可以用M盘 (球)状半径R与M和m之间的距离 (L)的比值的ψ次方表示 (R与L在同一直线上),那么万有引力的新表述公式如下:
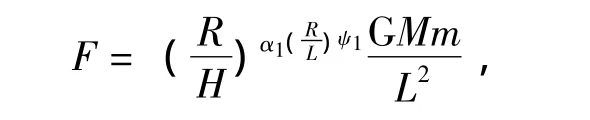
或
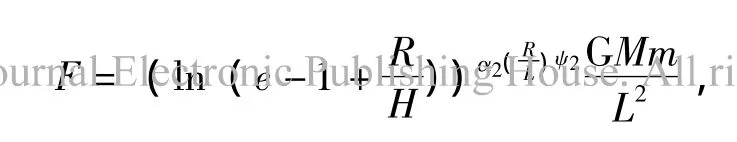
又或
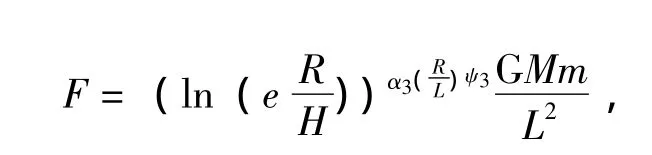
这里的R要表述为质量为M的物质的盘 (球)状半径。当R与L有一定夹角时可采用下面更普遍的公式
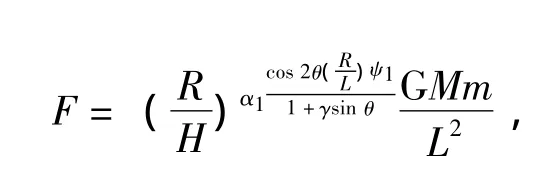
或
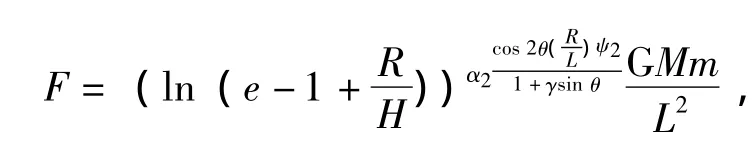
又或
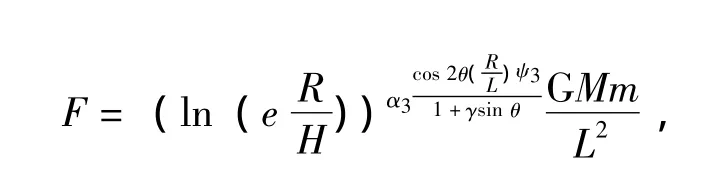
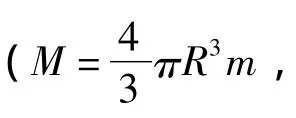
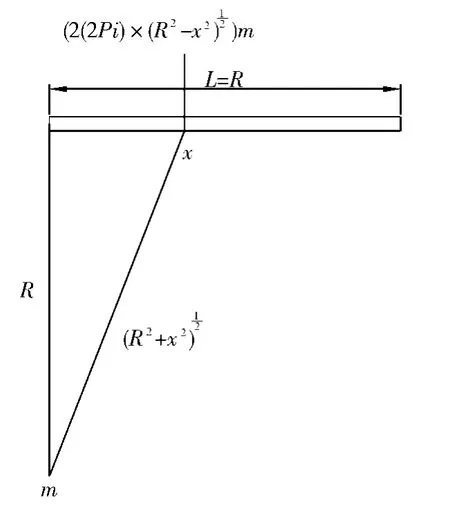
图3 r的求解图示
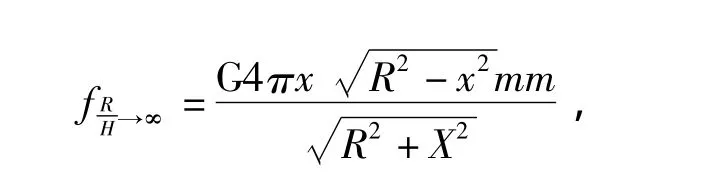
将R/H趋于无穷大,由积分公式得到的值代入上面的表述公式即可得到λ与R/H的关系 (过程太复杂)。通过代值法可以大概得到λ在R/H<1 000(四位)时取3或π,R/H>1 000(四位)时取位数值+零点 (首位数+2)。由此可以近似的认为λ为一定值3或π。
三个公式的选取和ψ、γ的准确值都要通过大量精确的观测和实验来确定。而由多次观测和实验的结果可做出F与L、H、R、θ的关系曲线,从而可以给出一个更精确的公式来表示出它们的关系是完全有可能的,进而给出一个万有引力更精确的表述。
牛顿的万有引力公式是从行星运行的三大定律用数学方式严格推导的。但从行星运行的三大定律中可知,万有引力本应有的非固定系数 (质量分布系数)在描述行星运动的三大定律中非常接近于1(即K趋于0)。这在万有引力的数学推导中几乎是没有任何影响。但万有引力推导的公式结果应用在星系的边沿星的受引力情况时不严格成立,因为在边沿星的引力计算中,系数和1差别很大 (几乎都是大于1)。这本来应有的“多余”万有引力却被牛顿公式计算结果解释为存在大量“暗物质”产生的结果。
将质量分布系数代入爱因斯坦计算水星冲日[6]的公式中可以继续修正水星的进动值 (与银盘大旋共同修正,偏差可缩小到1角秒以内)。
6 剩余力效与星系团相对运动的力效分析与解释
此文章并不是绝对反对宇宙中 (特别是星系中)存在大量的暗物质,而是反对将观测到的多余力效盲目的认为是暗物质造成的。
由上面推导的万有引力增效和星系内的黑洞 (不发光的星体,其实也不能称其为暗物质)可以或多或少的解释星系边沿恒星所受的多余向心力,而不能完全解释的一部分和星系间的相对旋转运动的多余向心力也许是由暗物质产生的,又或者是由弦与物质的作用力 (另文详述)。
[1]LIZ,Kruesi.关于暗物质我们究竟知道些什么[OL].[2010 -05 -24].http://songshuhui.net/archives/38069.html.
[2]马文蔚,周雨春.物理学教程[M].北京:高等教育出版社,2006.
[3]同济大学应用数学系.高等数学[M].上海:高等教育出版社.2002.
[4]胡宁.广义相对和引力场理论[M].周口:科学出版社,1999.
[5]叶壬癸.狭义相对论入门[M].厦门:厦门大学出版社,1988.
[6]黄黎红.科学技术导论[M].莆田:成都-电子科技大学出版社,2009.
The Mystery of Dark Material
REN Hai-tao
(Department of Electronic Information Project,Putian University,Putian 351100,China)
The theory is Extrapolated by observed running rate of the cluster of galaxies in the universe including the massive dark material,as if it obtains recognition between the majority of physical and the astronomical academic field.But I actually do not recognize the synchronous theory,because there are not the greatly massive dark materials in fact.As long as we calculates one by one again each star of entire galaxy to the star gravitation of galaxy border and the statistical attraction effect,we can obtain the attraction value which the border star detours needs.The increase of the gravity is due to limb effect and power bridge effect increasing sharply,so we propose a new formulation of gravity.
Dark material;gravitation;statistics;effect
O372;P131
A
1009-0312(2012)01-0024-06
2011-06-30
任海涛 (1986—),男,四川遂宁人,主要从事理论物理研究。

