低冗余度多输入多输出雷达阵列结构设计

王 伟 马跃华 王咸鹏

（哈尔滨工程大学自动化学院，黑龙江 哈尔滨 150001）

引 言

多输入多输出（MIMO）雷达作为一种新型的雷达体制，已经成为人们研究的热点［1－3］。MIMO雷达在发射端发射相互正交的波形，再在接收端通过一组匹配滤波器将其分离，可以形成一个虚拟阵列［4］。虚拟阵列技术给 MIMO雷达带来了诸多优势，如更高的空间分辨率［5］、增强的抗干扰能力［6］、更多的可分辨目标数目［7］，以及更灵活的波束方向图设计［8－9］等。但同时，为了得到虚拟阵列所必需的正交波形发射以及接收端的匹配滤波器组等条件，都增加了MIMO雷达的成本。如何利用有限的发射阵元和接收阵元产生最优的虚拟阵列是提高MIMO雷达性能和节约系统成本的关键。

早期的MIMO雷达文献多采用均匀线阵，陆珉等［10］提出了一系列准则来设计发射和接收阵列使得MIMO雷达虚拟阵列为均匀线阵，以方便利用传统的方法进行波达方向（DOA）估计。不过由于非均匀线阵在空间分辨率等方面的优势，近年来非均匀线阵在MIMO雷达中的应用正受到越来越多的关注。Bliss等［5，11］首先提出采用非均匀阵列可以大大扩展虚拟阵列的孔径，并给出了一种发射／接收阵列配置方法，以得到具有最长连续子阵的虚拟阵列。Chen等［12］将最小冗余的概念引入到 MIMO雷达中，并采用穷尽搜索算法寻求发射／接收阵列结构以形成最小冗余的虚拟阵列。张娟等［13］考虑收发同阵的情况下，利用最小实际物理阵元数形成最大孔径的低冗余虚拟阵列。以上几种MIMO雷达阵列结构设计方法［11－13］都是采用穷尽搜索算法以寻求最优的发射和接收阵列结构，这种算法运算量非常大，只适合阵元数较少的情况。董健等［14］提出一种基于差集和循环差集组合的MIMO雷达阵列结构设计方法来形成最小冗余虚拟阵列，这种方法虽然避免了阵元位置选择时的复杂运算，但当总的阵元数较大时，不同的发射阵元数和接收阵元数组合增多，如何在其中寻找使虚拟阵列孔径最大的组合值得研究。

本文提出一种新的阵列结构设计方法，该方法利用最小冗余阵组合来设计发射和接收阵列结构，使得MIMO雷达虚拟阵列为最小冗余阵，由于最小冗余阵已经得到广泛应用和深入研究［15］，所以利用这些已有的最小冗余阵进行组合来设计MIMO雷达阵列避免了复杂的阵元位置选择过程，易于工程实现，可以用于大阵元数的MIMO雷达阵列结构设计；另外在此基础上，本文还分析了在总的物理阵元数给定的情况下，如何分配发射阵元数和接收阵元数可以使虚拟阵列具有最大的孔径，使得本文所提方法更加简单实用。

1 最小冗余虚拟阵列模型

考虑MIMO雷达工作在窄带远场条件下，发射阵列和接收阵列位于同一直线。M个发射阵元位置关于半波长的归一化坐标表示为｛uT，m｝，m＝1，2，…，M；N个接收阵元位置关于半波长的归一化坐标为｛uR，n｝，n＝1，2，…，N。M个发射波形为φ（t）＝［φ1（t），…，φM（t）］T，发 射 波 形 满 足 正 交 条件，即

式中：T0为雷达脉冲宽度；IM表示M×M的单位阵；（·）T和（·）H分别表示矩阵转置和共轭转置。

假设远场点目标方位为θ，则N个接收阵元接收到的目标响应可表示为

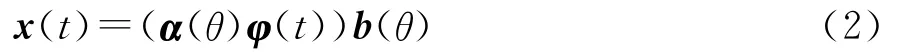
式中：α（θ）＝［exp（juT，1πsinθ），…，exp（juT，Mπsinθ）］和b（θ）＝［exp（juR，1πsinθ），…，exp（juR，Nπsinθ）］为相应的发射和接收导引矢量。

对每个接收阵元的接收信号关于M个发射波形进行匹配滤波，分离出来的信号的总数为NM。第n个接收阵元处对第m个信号的匹配滤波结果为

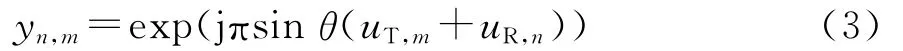
NM个分离出来的信号可以看作是一个等效阵列的接收信号，这个等效阵列的阵元坐标可以表示为

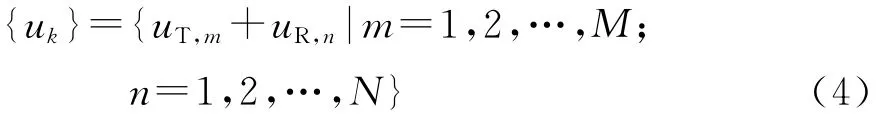
NM元的阵列就是MIMO雷达的虚拟阵列，而实际使用的实际物理阵元数只有M＋N个，这大大增加了MIMO雷达的自由度，给MIMO雷达带来了更高的角度分辨率和更好的性能。

为了使MIMO雷达的虚拟阵列为最小冗余阵，根据最小冗余阵的定义，需要有

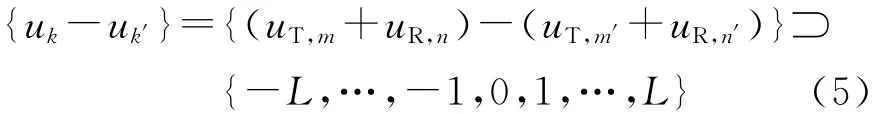
式中：k，k′＝1，2，…，NM；m，m′＝1，2，…，M；n，n′＝1，2，…，N；L为最小冗余阵的最大孔径。

MIMO雷达阵列设计问题可以描述为如何利用有限的物理阵元来产生具有最大孔径的最小冗余虚拟阵列，如式（6）所示

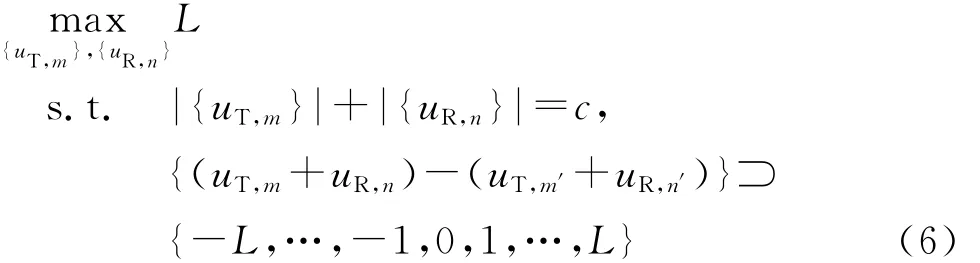
式中：｜｛·｝｜表示集合的势；c是总的物理阵元数。

这是一个关于点集的优化问题。当阵元数较少时可以采用穷尽搜索算法进行求解，但是随着阵元数的增加，搜索空间急剧增加，运算量增大，使得这种算法不适用于阵元数较大的情况。本文使用最小冗余阵组合的方法给出这个优化问题的一种最优解形式。

2 阵列结构设计

优化问题（6）中的第二个约束条件可以变换为

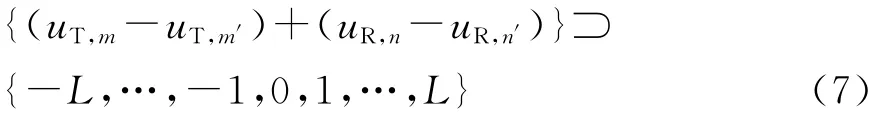
在此，令接收阵列为最小冗余阵，根据最小冗余阵定义有

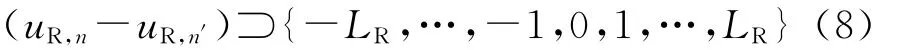
式中：LR为此最小冗余接收阵列的最大孔径。

在此条件下，式（7）中的第二项｛（uR，n－uR，n′）｝包含所有［－LR，LR］之间的整数。可以通过设计式（7）中的第一项使得其中不同元素与第二项的和无冗余，并且同时满足两项和包含［－L，L］之间的所有整数。设第一项中任意两个相邻元素为vk，vk＋1，vk＋1＞vk，则它们应该满足如下条件

可得，vk＋1－vk＝2LR＋1，所以第一项集合可以表示为

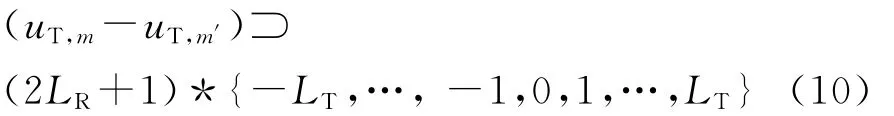
可见，此发射阵列为间距扩展了2LR＋1倍的最小冗余阵，其中LT为发射最小冗余阵的最大孔径。所以可以得出这样的结论：令MIMO雷达接收阵列为最小冗余阵，发射阵列为间距扩展2LR＋1倍的最小冗余阵，所得虚拟阵列也为最小冗余阵，最大孔径长度为（2LR＋1）＊LT＋LR.

讨论在给定总的阵元数的情况下如何配置发射阵元数和接收阵元数以使最小冗余虚拟阵列孔径最大。

根据最小冗余阵性质，可知LR≤N（N－1）／2，LT≤M（M－1）／2，取LR和LT的极大值做近似，则最小冗余虚拟阵列的最大孔径长度可以表示为

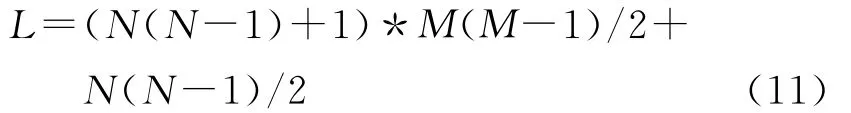
将c＝M＋N带入式（11），则有

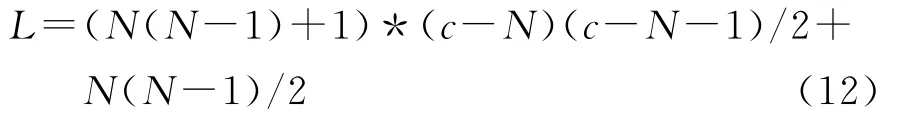
这是一个关于N的一元四次方程，通过数学分析可知极大值出现在N＝c／2附近。所以，在给定总的阵元数的情况下，为了得到最大孔径的最小冗余虚拟阵列，发射阵元数目和接收阵元数目应尽量接近，具体可按下式分配：

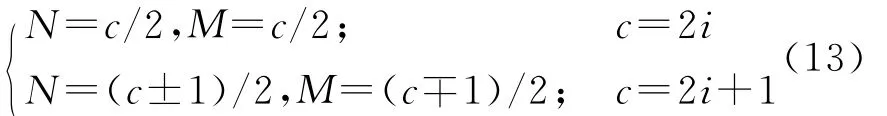
式中i为自然数。

为了得到最小冗余的虚拟阵列，MIMO雷达阵列结构设计具体步骤可以总结如下：

首先，在给定总的物理阵元数c情况下，根据式（13）确定接收阵元数N与发射阵元数M；然后令N元接收阵列为最小冗余阵，M元发射阵列为间距扩展了2LR＋1倍的最小冗余阵，最后，得到的MIMO雷达虚拟阵列即为最小冗余阵。

从上述MIMO雷达阵列结构设计过程可以看出，本文所提阵列设计方法是在已有的最小冗余阵的基础上通过简单的变换组合来实现虚拟阵列的低冗余度，该方法简单易于工程实现，可以用于大阵元数的MIMO雷达系统，同时具有很高的阵元利用率。

3 实验仿真

为了分析本文设计的阵列结构的性能，并与文献［14］中设计的阵列比较，对两种阵列结构下 MIMO雷达的波束方向图进行了仿真。仿真时，MIMO雷达总的阵元数为8，利用本文提出的阵列结构设计方法，发射阵元数和接收阵元数都取为4，接收阵列取为最小冗余阵，关于半波长归一化的坐标为｛uR，n｝＝ ｛0，1，4，6｝，发射阵列为间距扩展了（2＊6＋1）倍的最小冗余阵，关于半波长归一化的坐标为｛uT，m｝＝13＊｛0，1，4，6｝＝ ｛0，13，52，78｝.文献［14］中提出的一种阵列结构的发射阵元和接收阵元关于半波长归一化的坐标可以分别表示为｛uT，m｝＝｛0，21，36｝，｛uR，n｝＝｛0，3，4，9，11｝.各发射阵元发射相互正交的信号，并在接收端进行匹配滤波分离出来。期望的远场点目标方向为0°，信噪比为－5dB.采用最小方差无失真（MVDR）波束形成器。由于主要关心的是主波束宽度和最高旁瓣水平，所以图1只给出了两种阵列结构下MIMO雷达在（－20°，20°）之间的波束方向图。

从图1可以看出，在给出的两种阵列结构中，本文设计阵列结构下的MIMO雷达具有更窄的主波束宽度，但两者相差不大；另外可以看出，两个波束方向图的第一旁瓣电平也几乎一样。从波束方向图可以直观的看出，采用本文所提方法设计的阵列结构和文献［14］中设计的阵列结构的MIMO雷达系统具有几乎相同的性能。

表1给出了不同物理阵元数情况下，采用两种不同的阵列结构设计方法可以得到的MIMO雷达虚拟阵列的最大孔径，并比较了波束方向图－3dB主波束宽度。

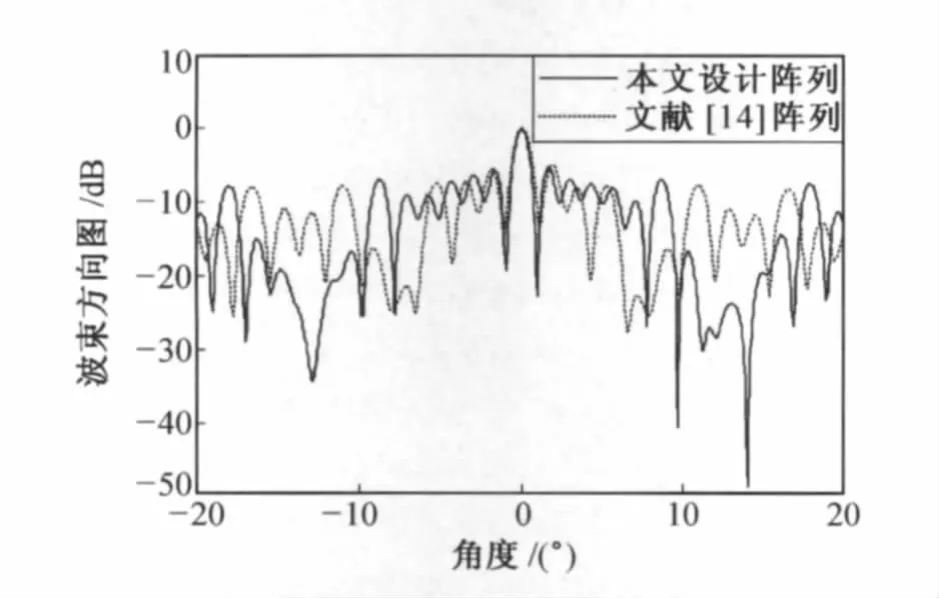
图1 两种阵列结构下MIMO雷达的波束方向图

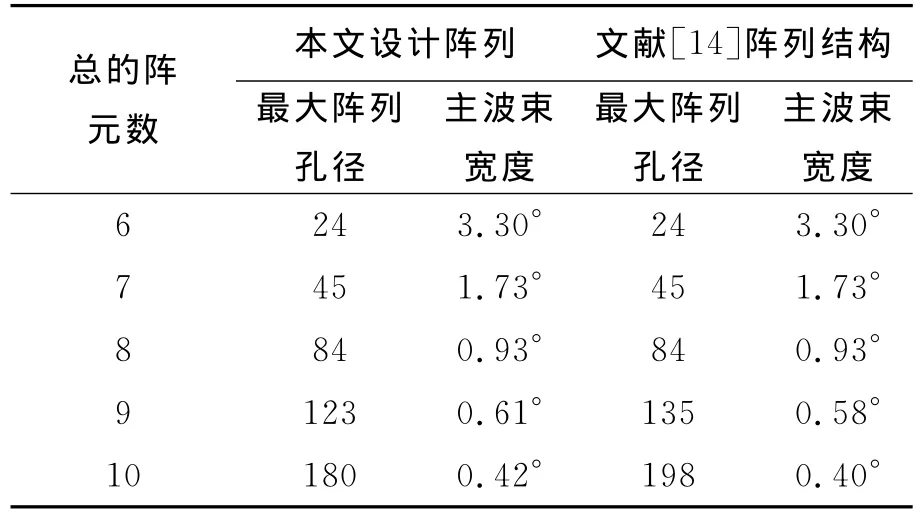
表1 不同阵元数的阵列孔径和主波束宽度

从表1可以看出，当总的阵元数小于等于8时，本文所提方法与文献［14］中的方法可以得到完全相同的虚拟阵列孔径以及主波束宽度；当物理阵元数大于8时，本文所提方法得到的虚拟阵列的孔径略小于文献［14］中的方法，这是因为不存在阵元数大于5的最优最小冗余阵，也就是说当总的阵元数大于8时，发射阵列或者接收阵列会出现一定程度的冗余，减小了阵列孔径。不过，由于孔径长度变化不大，所以对于空间分辨率影响并不大。从表1还可以看出，当总的阵元数为9时，主波束宽度变化仅为0.03°；当总的阵元数为10时，主波束宽度相差为0.02°.所以整体而言，两种阵列结构设计方法都可以使MIMO雷达具有很高的空间分辨率，不过由于本文所采用的是在工程中广泛应用的最小冗余阵进行组合，所以本文提出的阵列结构设计方法易于工程实现。

表2以总的阵元数等于8为例，分析了不同发射阵元数目与接收阵元数目的配置对MIMO雷达虚拟阵列孔径的影响。

从表2可以看出当接收阵元数和发射阵元数都为4时，虚拟阵列孔径最大，这验证了前面提到的设计准则，即在设计MIMO雷达阵列时应尽量使发射阵元数目与接收阵元数目相同，这样可以获得最大孔径的虚拟阵列，从而进一步提高阵元的利用率。这一准则也使得本文提出的阵列结构设计方法具有重要的实用意义，因为设计系统时需要考虑的一个重要因素是成本问题，在成本一定的情况下，所能获得的总的发射阵元和接收阵元（包括相应的发射机和接收机）的数目也就确定了，这一准则可以使MIMO雷达利用有限的成本获得最大的虚拟阵列孔径和最高的空间分辨率。

表2 不同发射和接收阵元数配置时的阵列孔径

4 结 论

本文提出了一种基于最小冗余阵组合的MIMO雷达阵列结构设计方法，可以使MIMO雷达虚拟阵列为最小冗余阵。另外，研究了在给定阵元数的情况下，如何分配发射阵元数和接收阵元数使MIMO雷达虚拟阵列孔径最大。本文提出的方法避免了复杂的阵元位置搜索过程，简单易于实现，阵元利用率高，可以用于大阵元数的MIMO雷达系统，具有重要的实用意义。

［1］FISHLER E，HAIMOVICH A，BLUM R，et al.MIMO radar：an idea whose time has come［C］∥ Proc IEEE Radar Conf.Pennsylvania，2004：71－78.

［2］郭艺夺，张永顺，童宁宁，等.一种 MIMO雷达二维DOA估计新方法［J］.电波科学学报，2010，25（4）：668－673.

GUO Yiduo，ZHANG Yongshun，TONG Ningning，et al.A novel method of 2－D DOA estimation for MIMO radar［J］.Chinese Journal of Radio Science，2010，25（4）：668－673.（in Chinese）

［3］刘红明，何子述，李 军.双基地MIMO雷达发射阵目标角度估计［J］.电波科学学报，2010，25（3）：499－504.

LIU Hongming，HE Zishu，LI Jun.Target angle estimation relative to transmitting array in bistatic MIMO radar［J］.Chinese Journal of Radio Science，2010，25（3）：499－504.（in Chinese）

［4］BEKKERMAN I，TABRIKIAN J.Target detection and localization using MIMO radars and sonars［J］.IEEE Trans on Signal Processing，2006，54（10）：3873－3883.

［5］BLISS D W，FORSYTHE K W.Multiple－input multiple－output（MIMO）radar and imaging：degrees of freedom and resolution［C］∥ 37th Asilomar Conf on Signals，Systems and Computers.California，2003：54－59.

［6］CHEN C Y，VAIDYANATHAN P P.MIMO radar space－time adaptive processing using prolate spheroidal wave functions［J］.IEEE Trans on Signal Processing，2008，56（2）：623－635.

［7］LI J，STOICA P，XU L Z，et al.On parameter identifiability of MIMO radar［J］.IEEE Signal Processing，2007，14（12）：968－971.

［8］STOICA P，LI J，XIE Y.On probing signal design for MIMO radar［J］.IEEE Trans on Signal Processing，2007，55（8）：4151－4161.

［9］刘韵佛，刘 峥，谢 荣.一种基于拟牛顿法的发射方向图综合方法［J］.电波科学学报，2008，23（6）：1188－1193.

LIU Yunfo，LIU Zheng，XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on newtonlike method［J］.Chinese Journal of Radio Science，2008，23（6）：1188－1193.（in Chinese）

［10］陆 珉，许红波，朱宇涛，等.MIMO雷达DOA估计阵列设计［J］.航空学报，2010，31（7）：1410－1416.

LU Min，XU Hongbo，ZHU Yutao，et al.Array design of MIMO radar Estimation of DOA ［J］.Acta Aeronautica et Astronautica Sinica，2010，31（7）：1410－1416.（in Chinese）

［11］FORSYTHE K W，BLISS D W，FAWCETT G S.Multiple－input multiple－output（MIMO）radar：Performance issues［C］∥ 38th Asilomar Conf on Signals，Systems and Computers.California，2004：310－315.

［12］CHEN C Y，VAIDYANATHAN P P.Minimum redundancy MIMO radars［C］∥Proc ISCAS.Washington，2008：45－48.

［13］张 娟，张林让，刘 楠.阵元利用率最高的MIMO雷达阵列结构优化算法［J］.西安电子科技大学学报，2010，37（1）：86－90.

ZHANG Juan，ZHANG Linrang，LIU Nan.Array optimization algorithm for MIMO radar with a maximum physical sensors efficiency［J］.Journal of Xidian University，2010，37（1）：86－90.（in Chinese）

［14］DONG Jian，LI Qingxia，GUO Wei.A combinatorial method for antenna array design in minimum redundancy MIMO radars［J］.IEEE Antennas and Wireless Propagation Letters，2009，8：1150－1153.

［15］DONG Jian，LI Qingxia，JIN Rong，et al.A method for seeking low－redundancy large linear arrays in aperture synthesis microwave radiometers ［J］.IEEE Transaction on Antennas and Propagation，2010，58（6）：1913－1921.