雷达角闪烁的混沌特性研究

张 锦 苗俊刚 郑 成 谢 衍

（北京航空航天大学电子信息工程学院，北京 100191）

引 言

在对目标雷达特性的研究中，角闪烁和雷达散射截面（RCS）是同等重要的两种物理量，是雷达目标的特征信号［1］。角闪烁的概念与扩展目标的概念紧密相连。复杂目标不同部位的散射强度和相位会造成回波相位的畸变，回波波前在接收天线口面上的倾斜与摆动产生了角闪烁［2］。凡是尺寸与波长能比拟、具有两个或两个以上等效散射中心的任何体目标都会产生角闪烁线偏差，这类体目标称为扩展目标。角闪烁误差对目标跟踪和识别有较大影响，强角闪烁信号可能导致目标跟踪失败和误判，因此，如何预测和抑制角闪烁成为散射研究领域中的重要议题［3］。相关研究对角闪烁的后处理及抑制方法的讨论很多，但只有很少的文献涉及到角闪烁的混沌特性的详细判定及与标准模型的结果对照。因此，讨论角闪烁的混沌特性是一个新颖的课题。

首先采用相位梯度法对共线两散射中心和五散射中心模型的角闪烁进行了仿真计算，并用图形电磁学算法（GRECO）计算出了一个典型目标的螺旋运动角闪烁数据。随后设计了一个全面和细致的非线性和混沌验证流程算法，并对照业内公认的标准混沌模型Lorenz模型经过同样流程的仿真结果，对三种角闪烁计算结果进行了一系列混沌定性、定量判别，确定了角闪烁具有显著的混沌特性，为抑制角闪烁和目标识别拓展了新思路。

1 角闪烁精确建模

1.1 角闪烁精确建模

相关领域研究人员对雷达角闪烁的建模提出了几类方法，包括精确建模、统计建模等。为了验证角闪烁的非线性及混沌特性，采用相位梯度法对同轴共线多散射中心模型进行角闪烁仿真计算［3－5］，后续内容验证其混沌特性。

假设目标由排列在同一条直线上多个散射源组成，如图1所示，O是坐标原点，θ是水平面上观测角，散射中心排列在Z轴上。P是雷达位置，ri是第i个目标到雷达的距离。

雷达距离：

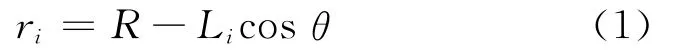
单个理想导体球体散射中心的散射场为［6］

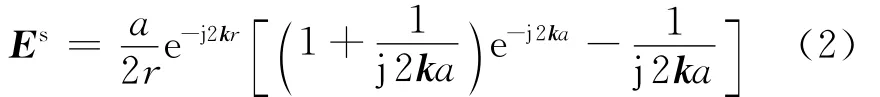
式中，a为球体直径，直径的大小代表了接收散射场的强度。设第i个散射中心的散射源幅度为Ai，相位为φi，则多个散射中心的后向散射总场为

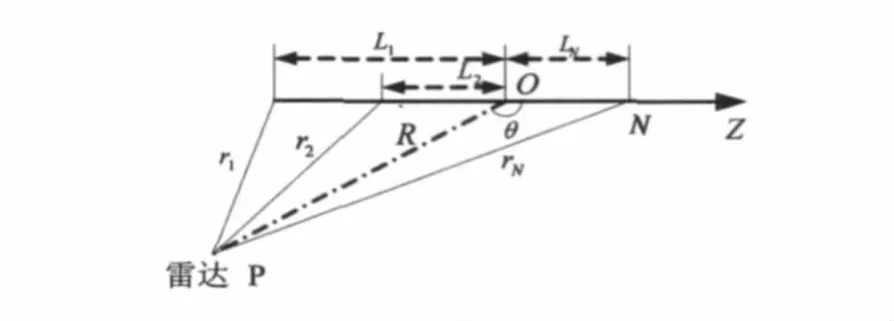
图1 共线多散射中心目标几何模型

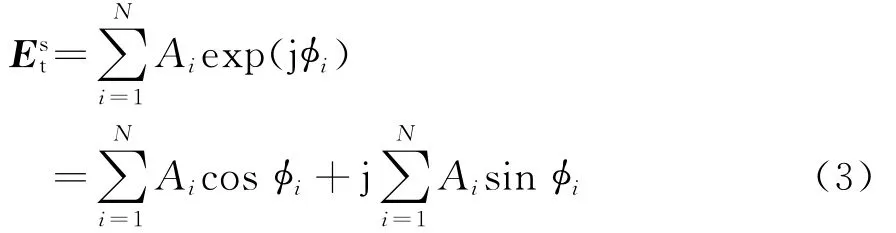
目标对观察点P处散射场相位为

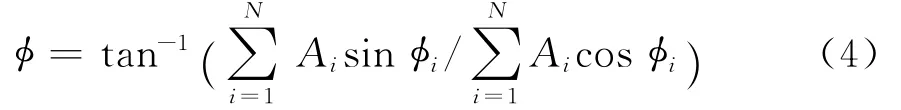
利用相位梯度法，可得俯仰面和方位面上的角闪烁计算方法如公式（5）所示。限于篇幅，本文只讨论方位面上方位面角θ变化时的角闪烁精确计算。双散射中心角闪烁建模采用两个与中心线等距且直径差距较小的散射中心作为建模模型，得到的结果具有较强的简单目标普适性。仿真参数设置为：f＝10GHz，R＝300m，L1＝－0.3m，L2＝0.3m，a1＝0.1m，a2＝0.15m（符合远场条件及散射中心体积与波长可比拟的条件），角闪烁量纲为米，仿真步长为0.01°，水平面角度扫描范围为0°～180°.为计算其时间序列特性，并与实际雷达扫描时的情景相匹配，图形坐标横轴采用时间序列的方式显示为雷达系统中的时域采样点数量。角闪烁仿真计算结果请见后文混沌特性分析中图5及图6.可见角闪烁曲线偏向中心正向的距离，即散射中心直径较大，产生较强角闪烁的方向，符合散射中心偏移理论。

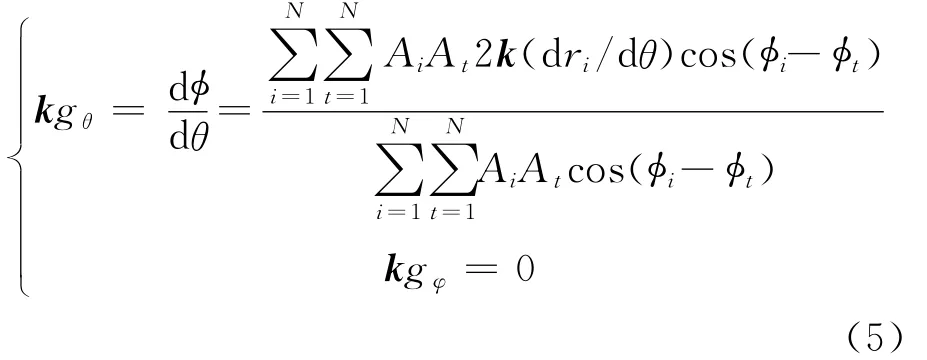
依相同方法可计算五散射中心目标的方位面面角闪烁：L1＝－0.3m，L2＝0.3m，L3＝0.6m，L4＝－0.5m，L5＝1m，a1＝0.1m，a2＝0.15m，a3＝0.1 m，a4＝0.3m，a5＝0.8m，其余参数不变，仿真结果如图3所示。按相关文献论述，五散射中心角闪烁已属复杂散射体［7］。

1.2 典型目标GRECO角闪烁计算

GRECO算法是对角闪烁精确建模的拓展，被电磁散射理论界公认为是与实际测量最为接近的仿真方法之一［6，8］，是相位梯度法在动目标图形化实时仿真系统中的应用，综合了物理光学法、物理绕射法、几何绕射法等常用电大尺寸目标的散射场计算方法［9－10］，将每个像素视为是一个散射中心，当目标在屏幕上显示后，所有像素点组成的散射中心模型即代表该复杂目标，通过获得每个散射中心的回波场强和位置信息求取复杂目标的角闪烁。

复杂目标由n个统计独立的散射中心组成，假定观察距离远大于散射中心与雷达间距和波长，则入射波可以近似看成是平面波，略去时谐因子后各散射中心被雷达接收的总回波信号为

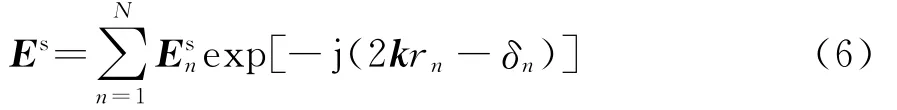
式中：rN表示第N个散射中心到接收雷达处的距离；，δn分别是第n个散射中心的幅度和初始相位。由此得到回波信号的总相位为

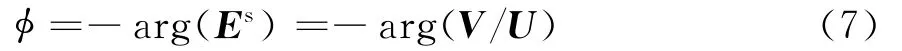
式中：

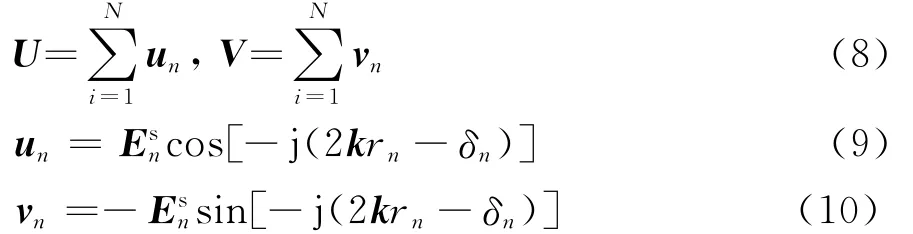
针对目标的每个实时姿态，由相位梯度法，可计算出水平面和俯仰面的角闪烁线偏差为

GRECO计算的目标模型采用公认的典型目标［8］，目标运动方式［10－11］选为螺旋运动（符合目标运动规律），目标和坐标设置如图2所示。

角闪烁计算参数如表1所示。

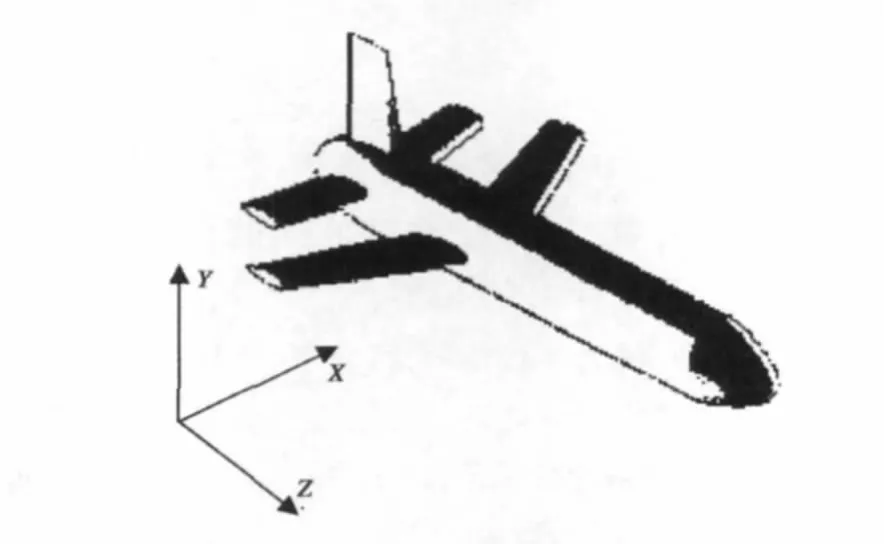
图2 典型复杂目标模型［8］

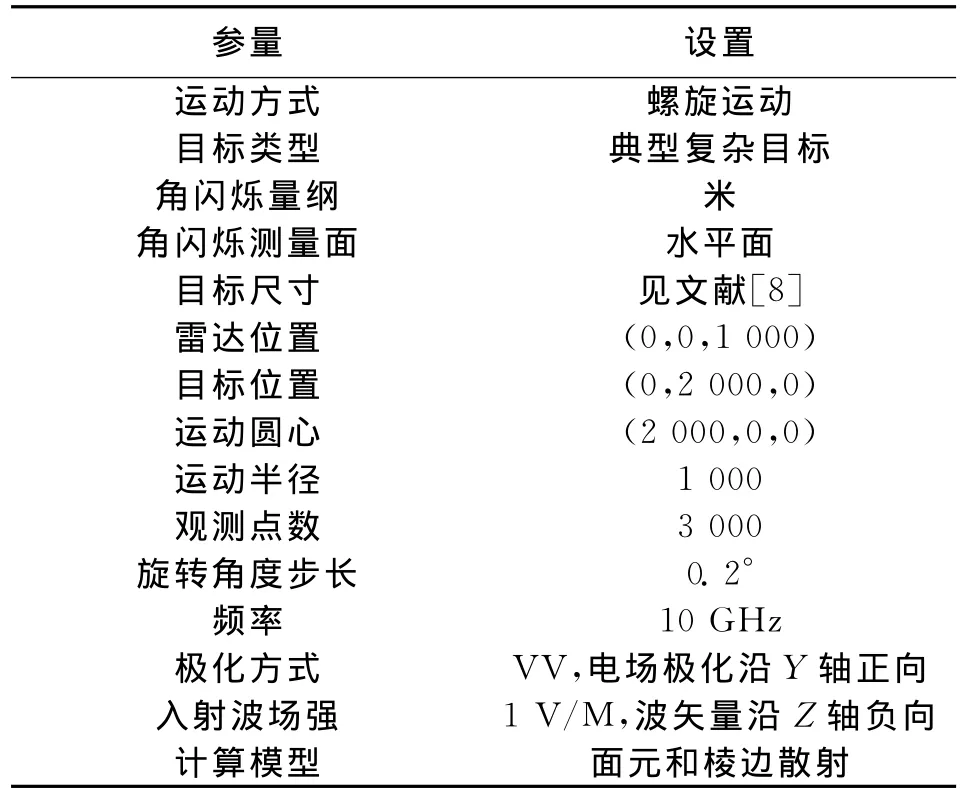
表1 典型目标角闪烁计算参数

由GRECO算法计算得到的角闪烁波形请见后文混沌分析中图7.

2 角闪烁时间序列的混沌验证

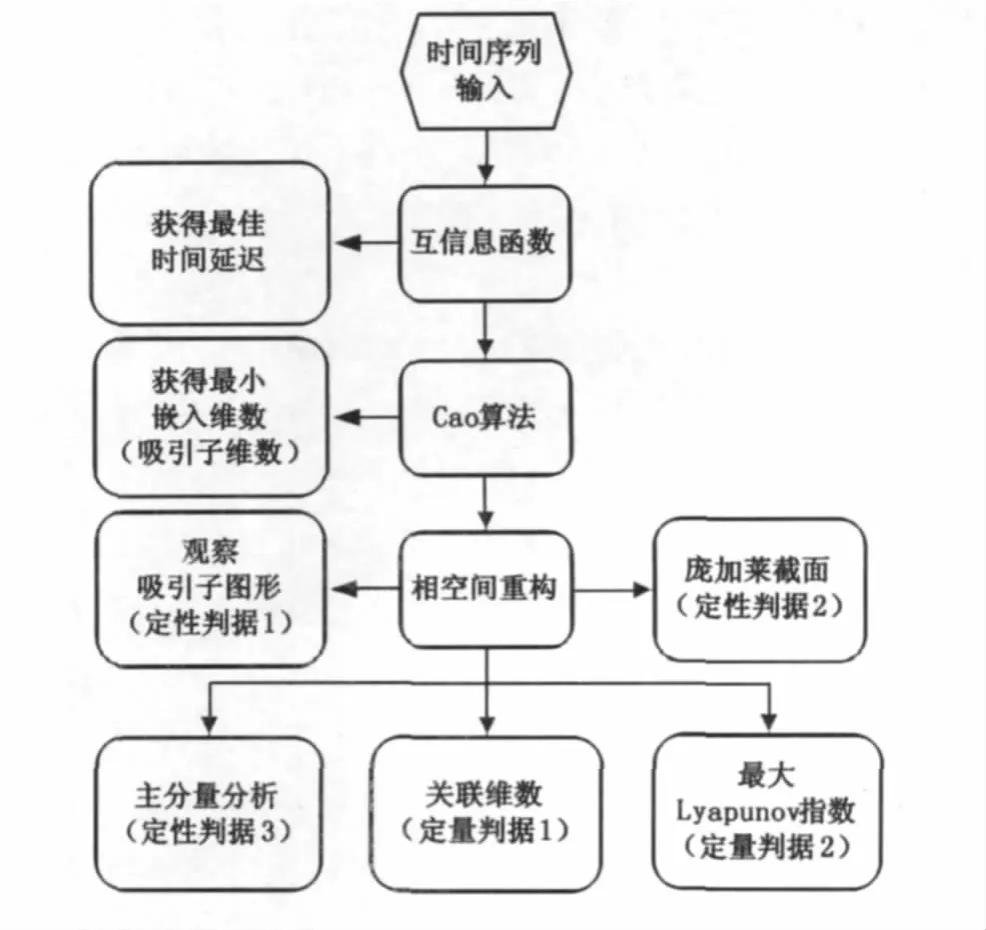
图3 混沌判定流程图

非线性科学与混沌理论是近年学术界热点，很多看似用常规方法无法解决的问题从非线性科学中都获得了崭新的解决思路。在经济学、地理、气象数据的处理和预测中，非线性与混沌理论已经获得了广泛的应用。本文参考国外非线性科学学者的权威成果［12－14］，利用混沌理论设计了一个全面和细致的验证流程算法（图3），并对照公认的混沌模型Lorenz吸引子的仿真结果，验证了角闪烁的混沌特性。

本流程中混沌特性的判定可依定性［12，14］和定量［15－16］分析算法分别验证，三个定性判据包括吸引子、庞加莱截面和主分量分析，两个定量判据包括关联维数和最大Lyapunov指数。后续分析将Lorenz吸引子和三种角闪烁序列均通过此流程验证，得到一系列定性和定量的判定结果。以下对此验证流程进行简要叙述。

1）互信息函数确定最佳时间延迟。取多个时间延迟进行平均信息量的迭代计算，得到的向量是延迟后以τ为自变量的时间序列重构；取其第一个最小值点对应的时间点作为延迟的估计值［12－13］。

2）Cao算法确定最小嵌入维数［17］。①采用上步求得的最佳时间延迟τ和d＋1（为待定嵌入维数）个嵌入维数作为输入参量，采用伪临近算法定义范数商参量，并将a参量加权求和且归一化得到参量并绘制其图形；②以a的第一个明显拐点作为最小嵌入维；③以τ和min－ed重构吸引子［15］并观察其运动特性。通常情况下，混沌的最小嵌入维数为2或者3，方能成功重构吸引子动力学特性。由此得到的吸引子图形为第一个混沌定性判据：吸引子在有限空间内不断伸长和折叠，构成回复性永不相交的非周期运动，具有良好的几何构型，则序列具有混沌特性。

3）相空间重构并生成二维庞加莱截面图［13－14，16］，即在相空间中适当选取一截面（要有利于观察系统的运动特征和变化，如截面不能和轨迹相切，更不能包含轨迹），称此截面为庞加莱截面，相空间的连续轨迹与庞加莱截面的交点称为截点。设记录得到的庞加莱点为：B0，B1，…，Bn，…。在庞加莱截面上使相空间轨迹连续运动，降为低维的离散点之间的映射，T称为庞加莱映射［16］。

由此得到的庞加莱截面图成为第二个混沌定性判据［17－18］，即：1）当庞加莱截面上有且仅有一个不动点或少数离散点时，序列是周期的；2）当庞加莱截面是一条封闭曲线时，序列是准周期的；3）当庞加莱截面上是一些成片的具有分形结构或良好几何构型的形体时，序列是混沌的。

4）依据关联积分G－P算法［18］选择最佳嵌入维数重构相空间［16］，并求得关联维数。步骤如下：1）按照前述计算得到最小嵌入维，并以此重构相空间，然后计算关联积分；2）不断增大嵌入维数并重新重构相空间，观察关联积分曲线图形，选择除去斜率为0和无穷的曲线中最接近直线的曲线，求得该曲线的斜率即为关联维数D；3）考察关联积分曲线的收敛性，若曲线在某嵌入维数以上呈发散状态并密集聚拢，则该嵌入维数即为最佳嵌入维数opt－ed.由此得到关联维数的定量混沌判据：如果关联维数是整数，则序列是准周期或随机的；如果关联维数不是整数，则序列是混沌的。

5）以最佳嵌入维数opt－ed重构相空间，进行主分量谱图分析［16，19］。由时间延迟和最佳嵌入维数重构相空间，求出轨线矩阵；计算协方差矩阵，并计算出其特征值和特征向量；将特征值按由大到小排列，则特征值和对应的特征向量称为该时间序列的主分量。求出特征值的和γ，以γ为纵坐标，嵌入维数1至opt－ed为横坐标绘制出的图形即为主分量谱图。由此得到主分量谱图判据：随机噪声序列的主分量谱图是一条与横轴接近平行的直线，而混沌序列则表现为一条沿负斜率下降的曲线，且在低维迅速下降。

6）Wolf法计算最大李氏（Lyapunov）指数［20］。该指数的计算方法为最小临近点算法。将重构相空间后的序列取一初始点，找到该点的最邻近点，追踪两点的时间演化，直到二者间距大于某门限值，保留该点并再寻找下一点，使距离小于该门限值，并且前两点与原始点连线的夹角尽可能小，对序列中每点重复上述过程直到序列终点，再用对数距离商的加权平均求得最大李氏指数。其定量判据为：若该指数大于零，则序列是混沌的。

3 仿真结果与分析

3.1 Lorenz模型的建立

Lorenz是典型的混沌系统，其迭代微分方程组为［15－16］：

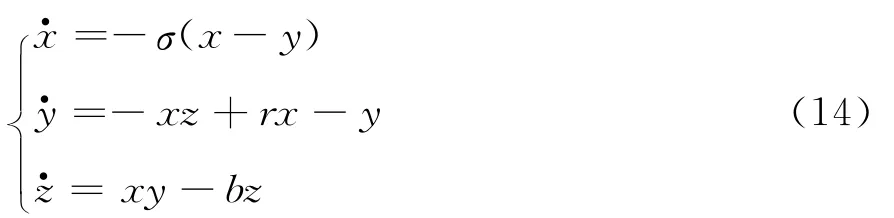
为清晰地分析角闪烁的混沌特性，以标准Lorenz模型作为对照模型，给出该模型和角闪烁模型在定性和定量特性上的相似点。参数设置为：序列长度与角闪烁同为18 000点，步长为0.025，σ，r，b的取值分别为0.1，－0.1，－0.02，考虑x分量序列，如图4左上角所示。在混沌定性验证分析中，所有轨迹均为归一化长度，故运动轨迹无量纲。

3.2 混沌定性分析结果比对与分析

如图4～7所示，混沌定性分析产生三个定性判据：吸引子图形，主分量分析和庞加莱截面。

从图4～7右上角吸引子图形可得，Lorenz模型与三个角闪烁序列吸引子结果均在有限空间内不断伸长和折叠，构成回复性永不相交的非周期运动，且具有良好的几何构型，从运动形态上均满足混沌序列的吸引子特性。

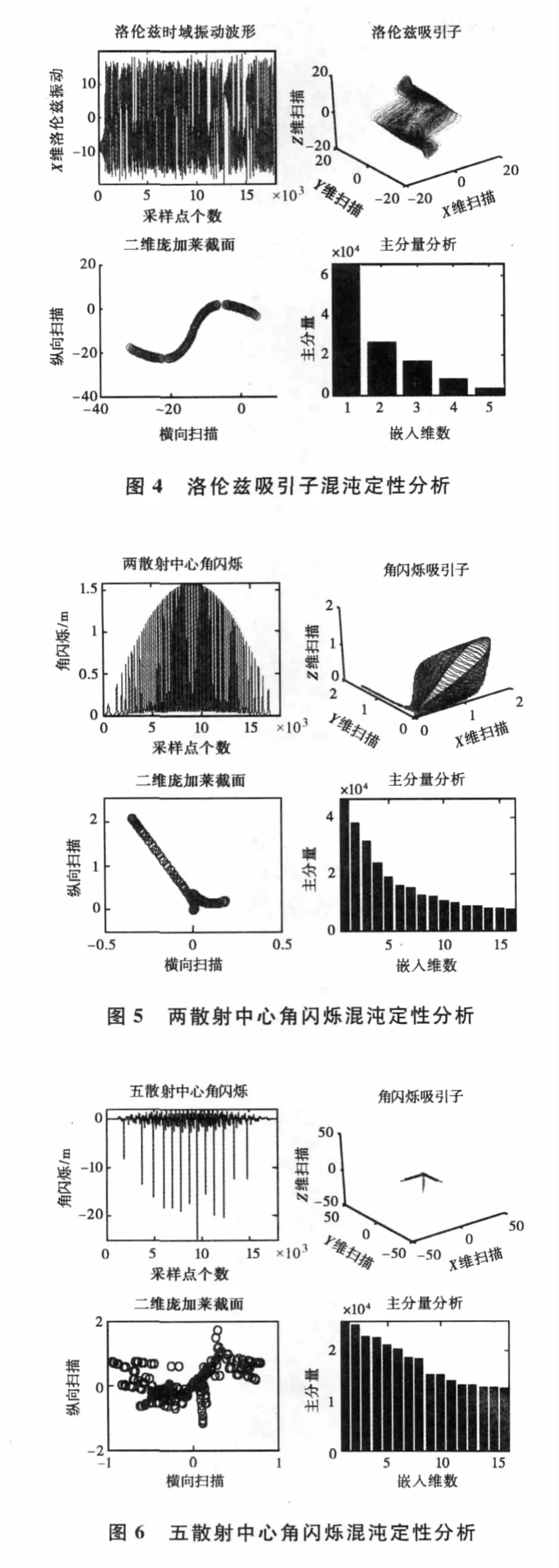
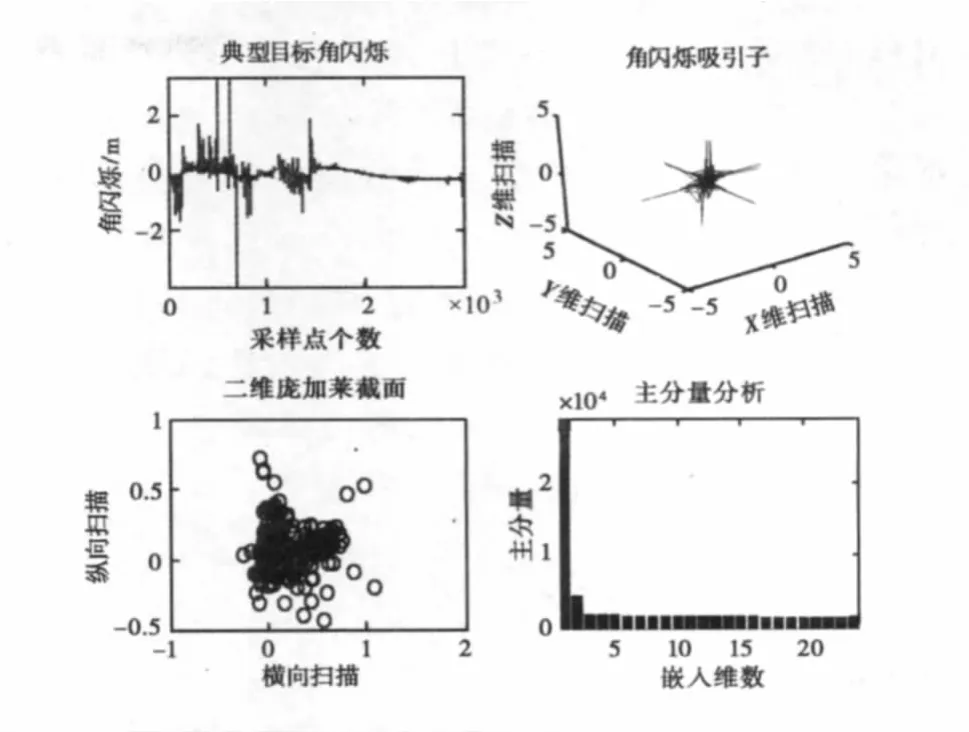
图7 典型目标角闪烁混沌定性分析

从图4～7左下角各图可得，四者的二维庞加莱截面图上均为成片具有分形结构的密集点，并且密集区域与非密集点区域有明显的界限，符合混沌序列的庞加莱截面特征。

从图4～7右下角各图可得，四者的主分量均具有沿负斜率下降的特性，并且在低嵌入维时主分量迅速下降（图7的主分量分析明显表现了该特征），故符合混沌的主分量谱图特性。

故由定性分析三个判据及判定标准，三组角闪烁序列具有明确的混沌特性。

3.3 混沌定量分析结果比对与分析

根据图3所示计算流程得到两种定量判据：关联维数和最大李氏指数的结果如表2所示，四者关联维数均为分数，最大李氏指数均大于零，且三组角闪烁序列的最大李氏指数与Lorenz系统的最大李氏指数处于同一数量级。故由定量分析的两个判据及判定标准，三种角闪烁序列均表现出明显的混沌特性。

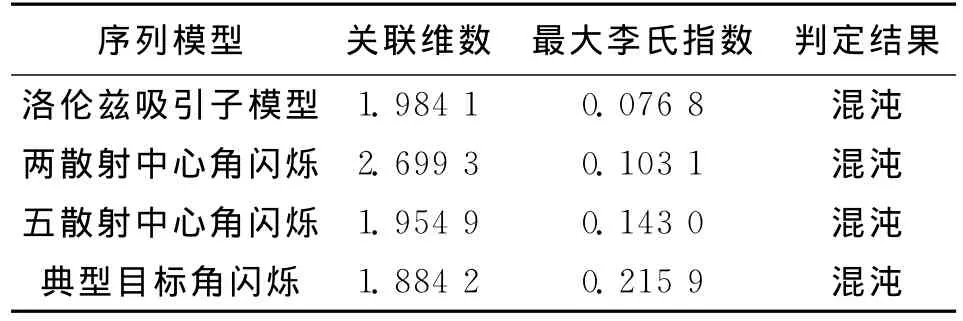
表2 混沌定量分析结果

4 结 论

为获得角闪烁原始数据，首先进行了同一直线上多散射中心目标的角闪烁仿真，并对典型目标采用GRECO算法进行典型目标动态角闪烁仿真，随后设计了详细的混沌验证流程，以Lorenz系统作为对照，从定性和定量两个方面验证了三个角闪烁模型的混沌特性。混沌相关研究表明：混沌具有短期可预测性，且可以依据相关算法对角闪烁进行抑制，从而达到减少丢失目标概率和提高目标识别能力的目的。因此，继续研究角闪烁的混沌特性及混沌抑制措施具有很高的理论和应用价值。

［1］HOWARD D D.Radar target glint in tracking and guidance system based on echo signal phase distortion［C］／／Proc of NEC，1959，5：840－849.

［2］王 涛，王雪松，肖顺平.一种极化测量雷达的角闪烁抑制方法［J］.电波科学学报，2004，19（6）：702－707.

WANG Tao，WANG Xuesong，XIAO Shunping.Suppressing the angular glint of polarimetric radar ［J］.Journal of Radio Science，2004，19（6）：702－707.（in Chinese）

［3］黄培康.雷达目标特征信号［M］.北京：宇航出版社，1993.

［4］SHI Xiaoli，LIU Yongcai.Angular glint of aircraft formation and its applications［C］／／IEEE ICMA.Harbin，5－8August，2007：1334－1339.

［5］王国玉，汪连栋.雷达目标角闪烁的建模与仿真.雷达火控技术，2000，29（2）：1－5.

WANG Guoyu，WANG Liandong.Modeling and simulations for radar angular glint［J］.Radar and Weapon Control，2000，29（2）：1－5.（in Chinese）

［6］方 宁，宁焕生，王宝发.复杂目标可视化角闪烁偏差计算［J］.北京航空航天大学学报，2006，32（2）：186－189.

FANG Ning，NING Huansheng，WANG Baofa.Visual computation of glint error for complex targets［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（2）：186－189.（in Chinese）

［7］DELANO R H.A theory of target glint or angular scintillation in radar tracking［C］／／Proc IRE，1952（12）：1778－1734.

［8］RIUS J M，FERRANDO M，JOFRE L.GRECO：graphical electromagnetics computing for RCS prediction in real time［J］.IEEE Antennas and Propagation Magazine，1993， 35 （2）： 7－17.doi：10.1109／74.207645.

［9］SUI Miao，XU Xiaojian.NFIPO based technique for near－field angular glint calculation of radar targets［J］.IEEE Transactions on Aerospace and Electronic Systems，2008，44（1）：372－380.

［10］曾永虎，王国玉，陈永光，等.动态雷达目标RCS的统计分析［J］.电波科学学报，2007，22（4）：610－613.

ZENG Yonghu，WANG Guoyu，CHEN Yongguang，et al.Statistical analysis for RCS of dynamic radar target［J］.Chinese Journal of Radio Science，2007，22（4）：610－613.（in Chinese）

［11］陈博韬，雷振亚，谢拥军，等.基于改进物理光学法的电大目标双站RCS的预估［J］.电波科学学报，2010，25（5）：960－965.

CHEN Botao，LEI Zhenya，XIE Yongjun，et al.Bistatic RCS prediction with improved PO method for electrically large targets［J］.Journal of Radio Science，2010，25（5）：960－965.（in Chinese）

［12］WOLF A，BESSOIR T.Diagnosing chaos in the space circle［J］.Physica D：Nonlinear Phenomena，1991，50（2）：239－258.

［13］MEISS J D.Asked questions about nonlinear science［R／OL］.［2011－10－13］http：／／amath.colorado.edu／pub／dynamics／papers／sci.nonlinearFAQ.pdf.

［14］CAMPBELL D K.Nonlinear Science from Paradigms and Practicalities［J］.Los Alamos Science，1987，15：218－262.

［15］李晓辉，李 湘，郭桂荣.扩展目标角闪烁非线性检验及其抑制技术［J］.系统工程与电子技术，2004，26（5）：592－595.

LI Xiaohui，LI Xiang，GUO Guirong.Nonlinearity detection and suppression technique for angle glint of extended targets［J］.System Engineering and Electronics，2004，26（5）：592－595.（in Chinese）

［16］MERKWIRTH C，PARLITZ U.TSTOOL User Manual Version 1.11［M／OL］.［2011－10－13］http：／／www.dpi.physik.uni－goettingen.de／tstool／manual.pdf.

［17］吕金虎，陆君安.混沌时间序列分析及其应用［M］.武汉：武汉大学出版社，2002.

［18］CAO Liangyue.Practical method for determining the minimum embedding dimension of a scalar time series［J］.Physica D：Nonlinear Phenomena，1997，110（1／2）：43－50.

［19］GRASSBERGER P，PROCACCIA I.Characterization of stranger attractors［J］.Phys Rec Lett，1983，50（5）：346－349.

［20］WOLF A，SWIFT J B，SWINNEY L，et al.Determining Lyapunov exponents from a time series［J］.Physica D：Nonlinear Phenomena，1985，16（3）：285－317.