基于稀疏互质L型阵列的二维测向算法

邵 华 苏卫民 顾 红 王 灿

（南京理工大学电子工程与光电技术学院，江苏 南京 210094）

引 言

在雷达、声纳和通信等领域，对辐射源进行定位［1－3］，常需要先确定入射信号的二维波达角（2DDOA，包括方位角和俯仰角）。针对2D－DOA估计问题，阵列信号处理中已有许多行之有效的方法被提出，例如二维多重信号分类法［4］（2D－MUSIC），但大多数测向方法只适合于等间距面阵。与等间距面阵相比，稀疏面阵能在不损失阵列孔径的前提下减小所需的阵元数，因此，研究稀疏面阵结构及其相应的波达角（DOA）估计算法具有极大的意义。

其中，文献［5］提出二维旋转不变（2D－ESPRIT）算法，它通过子阵间x轴和y轴的旋转不变关系估计方位角和俯仰角，缺点是需要3个结构相同的子阵，硬件成本高；基于此缺点，文献［6］、［7］利用四阶累积量［8－10］的阵列扩展特性，分别沿x轴和y轴构造与原阵列结构相同的虚拟阵列，然后再由2D－ESPRIT算法进行2D－DOA估计，即二维虚拟旋转不变（2D－VESPA）算法，然而其要求参考阵元间距（原阵列参考阵元和虚拟阵列参考阵元之间的间距）不大于信号半波长0.5λ；为突破阵元间距不大于0.5λ的限制条件，文献［11］、［12］提出嵌套阵列，文献［13］、［14］提出互质阵列，利用子阵间的嵌套或互质关系形成阵元间距不大于0.5λ的均匀矩形虚拟阵列，而允许物理阵元间距大于0.5λ.虽然这两种算法是利用虚拟阵元消除了测向模糊，但是其实质是仅采用一步就完成了解模糊。这导致正确解模糊时，系统允许两个阵元接收信号间相位差的测量误差（简称系统容差）较小。

针对以上问题，本文基于模转换［15］逐步解模糊的思想，首先构造了一类由两个具有相同互质结构的线阵组成的L型阵列，其中线阵1沿x轴放置，线阵2沿y轴放置；其次，利用一维虚拟旋转不变（1DVESPA）算法估计各基线所对应的模糊相位差；然后，结合基线间的互质关系逐步解模糊，分别得到x轴和y轴中最长基线对应的无模糊方向余弦；最后，采用x轴和y轴特征向量（估计不同坐标轴方向余弦时分别进行特征分解）间的对应关系，实现不同坐标轴方向余弦的匹配，最终得到方位角和俯仰角的估计值。与2D－VEPSA算法相比，本算法最大的优势在于利用基线间的互质关系突破0.5λ的限制条件，提高测向精度的同时保证较大的系统容差。

1 信号模型

如图1所示，L型阵列由x轴子阵（M＋1个全向阵元）和y轴子阵（M＋1个全向阵元）组成，两个子阵在坐标原点处共用阵元0，并且两子阵内相邻阵元间的基线长度分别为Dx，1，…，Dx，M和Dy，1，…，Dy，M，其中Dx，m＝Dy，m＝Dm，m＝1，…，M，基线D1最长，各基线之间满足如下比例关系

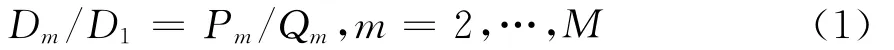
式中，Pm和Qm为互质的正整数，并且Q2＜…＜QM.

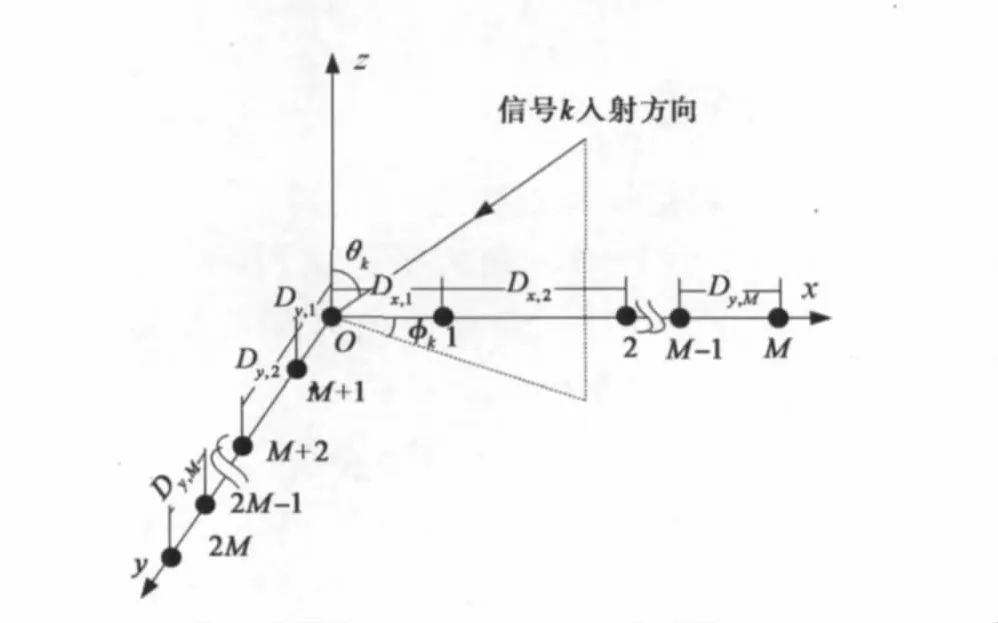
图1 L型阵列结构示意图

假设K个入射方向为（θ1，φ1），…，（θK，φK）的非高斯独立窄带远场信号源入射到上述阵元总数为2M＋1的L型阵列天线上，其中0≤φk＜2π和0≤θk＜π分别表示第k个入射信号的方位角和俯仰角。那么，L型阵列在t时刻接收的信号矢量为

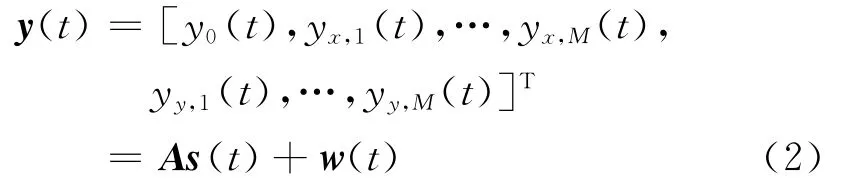
式中：yx，m（t）和yy，m（t）分别表示在x轴和y轴上第m个阵元的接收信号；s（t）＝ ［s1（t），…，sK（t）］T为信号向量；w（t）＝ ［w0（t），…，w2M（t）］T表示阵列接收噪声，噪声为平稳、时间和空间都互不相关的高斯白噪声，且与信号相互独立；A＝ ［a1，…，aK］是（2M＋1）×K维的阵列导向矩阵；ak＝］T，k＝1，…，K，其中

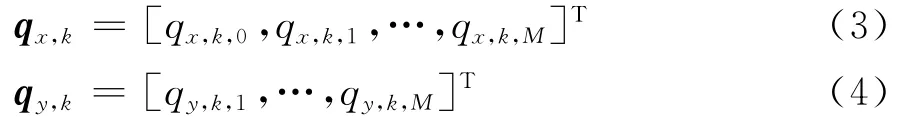
式中：qx，k，m＝exp（－jψx，k，m）和qy，k，m＝exp（－jψy，k，m），m＝1，…，M，其中ψx，k，m＝／λ和＝2πvkDy，m／λ，uk＝sinθkcosφk和vk＝sinθksinφk分别表示x轴和y轴方向余弦。当基线Dx，m＝Dy，m＞λ／2时，测量相位差φx，k，m∈ ［0，2π）和φy，k，m∈ ［0，2π）具有周期性模糊，即

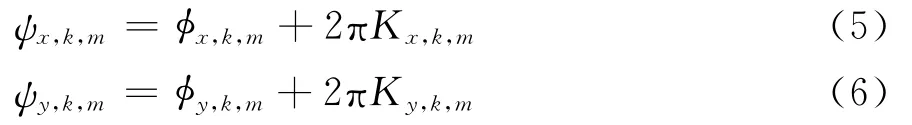
式中，Kx，k，m∈Z和Ky，k，m∈Z分别表示φx，k，m和φy，k，m的模糊数。这导致x轴和y轴测量方向余弦也具有模糊性。利用L型阵列输出的N个快拍数据进行无模糊2D－DOA估计。另外，为表述简洁，下文均省略时间t.

2 算法描述

2.1 四阶累积量矩阵的构造

利用图1中L型阵列的特殊结构，并结合四阶累积量的定义［7－10］及空间接收信号的数学模型，构造如下四阶累积量矩阵

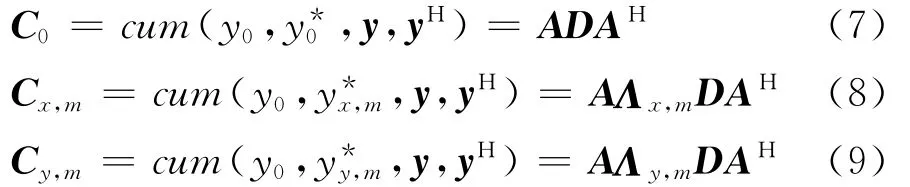
式中，m＝1，…，M，且

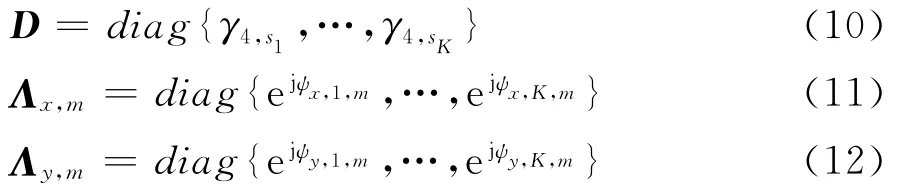
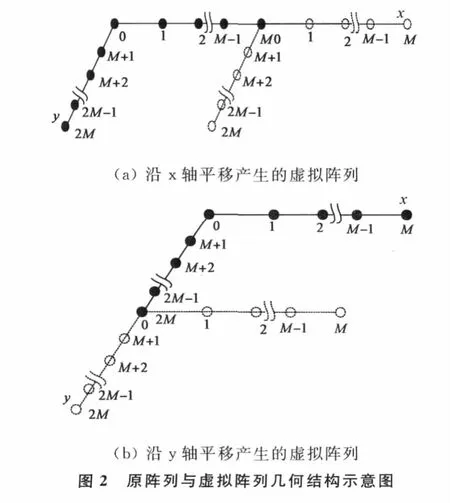
式中，γ4，sk表示第k个信号的四阶累积量。由四阶累积量的阵列扩展特性可知，式（8）表示的物理含义为：原阵列沿x轴平移xm距离后产生的虚拟阵列，如图2（a）所示，其中阵元m为虚拟阵列的参考阵元，称这类虚拟阵列为x轴虚拟阵列组；式（9）则表示原阵列沿y轴平移ym距离后产生的虚拟阵列，如图2（b）所示，其中阵元M＋m为虚拟阵列的参考阵元，类似的称其为y轴虚拟阵列组。为了估计所有相邻阵元间的相位差，选择阵元0作为原阵列的参考阵元，其他2M个阵元分别为2M个虚拟阵列的参考阵元，那么可以定义如下矩阵

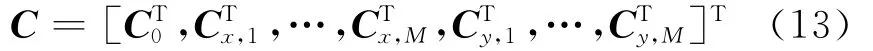
对式（13）进行奇异值分解（SVD）后，可得信号子空间Es＝ ［，…，，…，］T.

2.2 估计x轴基线对应的测量相位差

抽取A的相应行可以构造原阵列和x轴虚拟阵列组对应的导向矩阵Ax＝ ［AT，ATΛx，1，…，ATΛx，M］T.同样由Es可得它们对应的信号子空间Es，x＝ ［，，…，］T.因为Es，x和Ax都表示信号子空间，所以它们之间可以相互转换，令可逆矩阵T为转换矩阵，则Es

为了估计基线对应的测量相位差，令Fx，m＝（Es，x，m－1）†Es，x，m，m＝1，…，M，其中Es，x，0＝Es，0，并结合式（16）得

其中：（·）†表示矩阵伪逆；Λx，0是元素为0的K维方阵。对Fs，x，m进行特征分解后得Λx，m－Λx，m－1，求其对角元素的相位可得测量相位差的估计值＝，…］和特征向量Tx，m.

2.3 x轴方向余弦的估计

由于基线越长，测向精度越高。因此，为得到高精度x轴方向余弦估计，必须先通过模转换解模糊算法估计最长基线Dx，1对应的无模糊相位差。然而，由模转换解模糊算法的原理可知，它需要结合相同信号、不同基线所对应的测量相位差才能正确解模糊。又由x轴基线对应的测量相位差的求解过程可知，和是分别进行特征分解后得到的，其中m≠n，m∈1［］M，n∈［1M］，故和信号源三者之间的顺序具有任意性，所以对它们的配对是正确解模糊的前提。

根据矩阵的特征分解可知，特征值与特征向量是一一对应的，即和的配对问题转化成Tx，m和Tx，n的配对问题。假设表示Tx，m中第k1列向量表示Tx，n中第k2列向量，当它们对应 相 同 信 号 源 时，＝ 1，否 则≪1.基于以上分析，对Tx，m和Tx，n做如下操作其中，矩阵G中1的位置反映和间的配对关系。不失一般性，假设以的顺序为参考，利用上述方法分别对｛，m＝1，…，M｝进行配对后得

结合基线Dx，m和配对后的测量相位差估计值，m＝1，…，M，k＝1，…，K，利用模转换解模糊算法解最长基线D1，x对应测量相位差估计值φx，k，1的模糊，得到Dx，1对应的无模糊测量相位差，再经简单的计算后得高精度、无模糊x轴方向余弦估计值经过逐步解模糊得出，与单步解模糊相比，它能保证较大的系统容差较［15］。

2.4 y轴方向余弦的估计

与x轴方向余弦的估计类似，y轴方向余弦的估计分为以下几步：

1）由Es和A分别构造原阵列和y轴虚拟阵列组对应的信号子空间Es，y＝ ［，，…，］T和导向矩阵Ay＝ ［AT，ATΛy，1，…，ATΛy，M］T；

2）为了估计基线对应的测量相位差，m＝1，…，M，令

其中，Es，y，0＝Es，0，Λy，0是元素为0的K维方阵；

3）对Fs，y，m进行特征分解后得基线Dy，m对应测量相位差的估计＝［，…，］和特征向量Ty，m，m＝1，…，M；

4）以为基准，利用G＝，m，m＝2，…，M中1的位置对和进行配对，最后得到配对后y轴各基线所对应的测量相位差

5）对于第k个信号，利用模转换算法解模糊相位差的模糊数，得到无模糊测量相位差再经简单的计算后得高精度、无模糊y轴方向余弦估计

2.5 方位角和俯仰角的估计

由于和间并不一定对应同一信号源，因此，先对它们进行配对。与前面的配对类似，采用G＝中1的位置实现和的匹配，记匹配后的x轴和y轴方向余弦分别为和.根据方向余弦的定义，可得第k个入射信号方位角和俯仰角的估计值

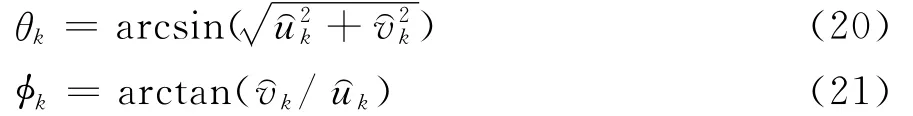
3 计算机仿真试验

通过计算机仿真来比较本文算法和2D－VEPSA算法的测向性能。由于本文算法要求各阵元间距满足一定的互质关系，而2D－VEPSA算法要求参考阵元间距不大于信号半波长，其他阵元位置任意，即它们对阵列结构的要求不同。因此，在仿真中，两种算法分别采用阵元数相同、结构不同的天线a和天线b来比较它们的测向性能，其中天线a是阵元间距满足互质关系的9阵元L型阵，各阵元都为全向阵，并且为了减小天线a的体积，已对辅助阵元的位置做了调整，但并不影响基线间的比例关系，如图3所示；天线b也是9阵元L型阵，其阵元1和阵元5的位置为 （λ／2，0，0）和（0，λ／2，0），其他阵元分布与天线a的相同，它作为天线a对比天线。

图3 仿真中本文算法采用的天线a

必须说明的是：在仿真中，本文算法首先以阵元0到阵元｛m，m＝1，…，4｝为参考阵元，形成与原阵列相距 ｛（Dm，0，0），m＝1，…，4｝的x轴虚拟阵列组，然后以阵元0到阵元｛m，m＝5，…，8｝为参考阵元，形成与原阵列相距 ｛（0，Dm，0），m＝1，…，4｝的y轴虚拟阵列组，利用虚拟阵列与原阵列间的旋转不变关系估计两坐标轴各基线对应的模糊相位差，经解模糊得到两坐标轴最长基线（D1）对应的无模糊方向余弦，简单计算后得三个信号的2D－DOA估计值；2D－VEPSA算法以阵元0、1和5为参考阵元，形成与原阵列相距 （λ／2，0，0）和（0，λ／2，0）的虚拟阵列组，利用虚拟阵列组与原阵列的旋转不变关系估计阵元0和阵元1及阵元0和阵元5之间对应的无模糊方向余弦，从而估计三个信号的2D－DOA.另外，仿真实验中使用均方根误差（RMSE）对算法测向性能进行评估，其中均方根误差定义为

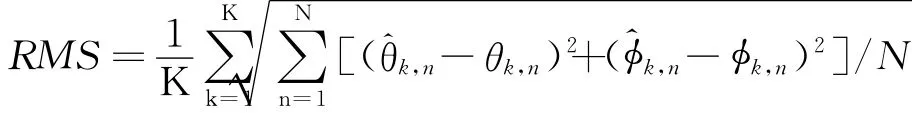
式中：和分别表示第k个目标俯仰角和方位角估计值；N表示Monte－Carlo试验次数。

仿真A：假设存在3个非高斯、独立、窄带远场信号源投射到这两个天线上，3个信源方位角分别为10°、20°和30°，俯仰角分别为15°、25°和35°，信源间相互独立，且与噪声互不相关，噪声为平稳、时间和空间都不相关的高斯白噪声。对于测量噪声，三个信号源有相同的信噪比（SNR），SNR取值范围为－10～20dB，取值步长为5dB，每次独立仿真采用2 000次快拍数据，独立重复200次Monte－Carlo试验。

如图4给出了两种算法的2D－DOA估计的RMSE随SNR的变化曲线。图5是本文算法中正确解模糊的概率随SNR的变化曲线。结合图4和图5可以看出，在正确解模糊的情况下（RSN≥0 dB），本文算法相对于2D－VEPSA算法在测向精度上具有较大改善，这主要是因为本文算法利用解模糊算法突破了2D－VEPSA算法中参考阵元间距不能大于半波长的限制，而测向精度与参考阵元的间距成正比，因此，本文算法能达到更高的测向精度。但是，当RSN＜0dB，本文算法的测向精度逐渐劣于2D－VEPSA算法，其原因是更低的信噪比超出了正确解模糊的系统容差，从而存在解模糊错误，导致本文算法测向性能急剧下降。

仿真B：假设两个阵列接收信号的SNR为10 dB，当快拍数从200变化到2 000，变化步长为200时，估计两种算法的测向性能随快拍数的变化，其他条件与仿真A相同。

如图6是两种算法的2D－DOA估计的RMSE随快拍数的变化曲线。很明显，两种算法的测向性能随快拍数的增大而提高，但变化的陡峭程度不如SNR.另外，本文算法测向 RMSE要小于2DVEPSA算法，其原因也是本文算法构造稀疏互质L型阵列，利用阵元间的互质关系解模糊，扩大阵列的孔径，提高测向精度。

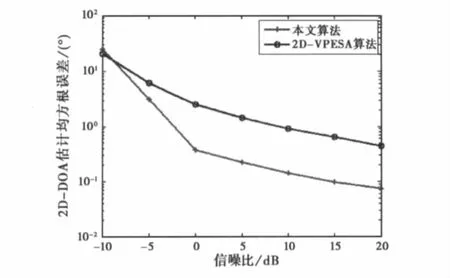
图4 两种算法的2D－DOA估计的RMSE随SNR的变化曲线

图5 本文算法中正确解模糊概率随SNR的变化

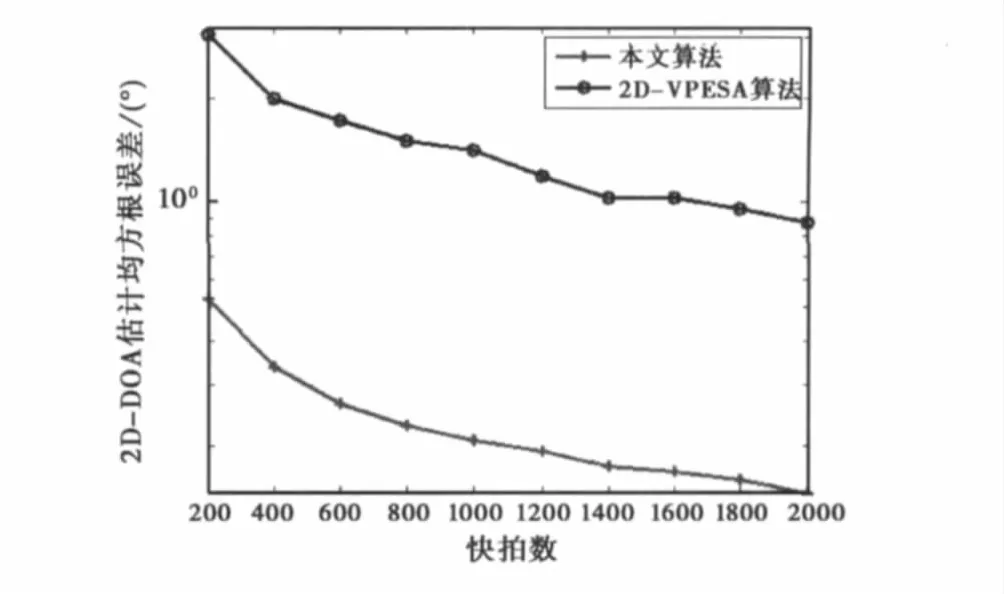
图6 两种算法的2D－DOA估计的RMSE随快拍数的变化曲线

4 结 论

提出了一种基于稀疏互质L型阵列的2D－DOA估计算法。与2D－VEPSA算法相比，利用阵元间的互质关系，解决测向精度与测向模糊之间的矛盾，扩大阵列孔径，提高测向精度，同时利用逐步解模糊，保证了较大的系统容差。

［1］DOGANCAY K. Relationship between geometric translations and TLS estimation bias in bearings－only target localization［J］.IEEE Transactions on Signal Processing，2008，56（3）：1005－1017.

［2］DOGANCAY K.Exploiting geometric translations in TLS based robot localization from landmark bearings［C］／／17th European Signal Processing Conference.Glasgow，Scotland，24－28August，2009：95－99.

［3］RAO S K，RAJESWARI K R，LINGAMURTY K S.Unscented Kalman filter with application to bearingsonly target tracking［J］.IETE Journal of Research，2009，55（2）：63－67.

［4］CHAN A Y J，LITVA J.MUSIC and maximum techniques on two－dimensional DOA estimation with uniform circular array［J］.IEE Proceedings Radar，Sonar and Navigation，1995，142（3）：105－114.

［5］KEDIA V S，CHANDNA B.A new algorithm for 2－D DOA estimation［J］.Signal Process，1997，60（3）：325－332.

［6］LIU T H，MENDEL J M.Azimuth and elevation direction finding using arbitrary array geometries［J］.IEEE Transactions on Signal Processing，1998，46（7）：2061－2065.

［7］DOGAN M C，MENDEL J M.Applications of cumulants to array processing－part I：aperture extension and array calibration［J］.IEEE Transactions on Signal Processing，1995，43（5）：1200－1216.

［8］齐子森，郭 英，王布宏，等.基于四阶累积量的共形阵列波达方向估计算法［J］.电波科学学报，2011，26（4）：735－744.

QI Zisen，GUO Ying，WANG Buhong，et al.DOA estimation algorithm for conformal array based on fourthorder cumulants［J］.Chinese Journal of Radio Science，2011，26（4）：735－744.（in Chinese）

［9］沈怡平，滕升华.基于四阶累积量的稳健盲波束形成算法［J］.电波科学学报，2008，23（6）：1056－1060.

SHEN Yiping，TENG Shenghua.Fourth－order cumulant based on robust blind beamforming algorithm［J］.Chinese Journal of Radio Science，2008，23（6）：1056－1060.（in Chinese）

［10］刘学斌，韦 岗，季 飞.基于四阶累积量扩展孔径的线阵设计［J］.电波科学学报，2006，21（1）：126－130.

LIU Xuebin，WEI Gang，JI Fei.Design of linear array with augmented aperture based on fourth－order cumulant［J］.Chinese Journal of Radio Science，2006，21（1）：126－130.（in Chinese）

［11］PAL P，VAIDYANATHAN P P.Nested arrays：a novel approach to array processing with enhanced degrees of freedom［J］.IEEE Transactions on Signal Processing，2010，58（8）：4167－4181.

［12］PAL P，VAIDYANATHAN P P.Two dimensional nested arrays on lattices［C］／／IEEE ICASSP.Prague，Czech Republic，May 22－27，2011：2548－2551.

［13］PAL P，VAIDYANATHAN P P.Sparse sensing with co－prime samplers and arrays［J］.IEEE Transactions on Signal Processing，2011，59（2）：573－586.

［14］VAIDYANATHAN P P，PAL P.Theory of sparse coprime sensing in multiple dimensions［J］.IEEE Transactions on Signal Processing，2011，59（8）：3592－3608.

［15］WILLETT P K.Modulo conversion method for estimating the direction of arrival［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36（4）：1391－1396.