基于FAHP和模糊综合评判的交通状态判别模型
陈义华,晏承玲
(重庆大学数学与统计学院,重庆 401331)
随着我国经济的飞速发展和城市化进程的加快,交通拥堵问题也变得日益严重。准确地识别道路交通状态是选取合适的交通控制策略的前提,也是交通诱导的需要,对于缓解局部拥堵并防止其演变为整个路网的拥堵有重要的现实意义。
目前,国内外学者基于模糊理论在道路交通状态判别方面已提出了大量的模型[1-7],其中大多是根据交通流的宏观参数及其衍生参数来建立。这些参数都能直接或是间接地反映交通运行状况,从而有效地对交通拥堵的程度做出评价。但是其中也存在着一些问题。首先,评价指标过多且具有一定的相关性,还有一些指标不易测量或难于被人们理解,这样既降低了模型的实用性又增加了计算复杂度。其次,在建立评价指标的隶属函数时,其阈值的选取过于主观随意。最后,确定评价指标权重的专家打分法或实践经验法不够合理。
本文根据交通流的分布特性以及交通拥堵的强度,将道路交通状态划分为4种:畅通、缓行、拥挤、堵塞。应用FAHP和模糊综合评判方法评判交通状态,提出了一种判别交通状态的模型。
1 交通状态评价指标体系
城市道路由路段和交叉口2个基本单元组成,而它们的交通特性各不相同,所以评价指标体系应该同时包含路段和交叉口指标。又结合交通流的运行特点,以对交通状态的变化敏感、定量化获取容易以及计算准确率高为依据选取了5个评价指标。
1.1 路段评价指标的选取
1.1.1 平均行程速度
平均行程速度V为车辆通过路段时路段长度与所用的全部时间之比,
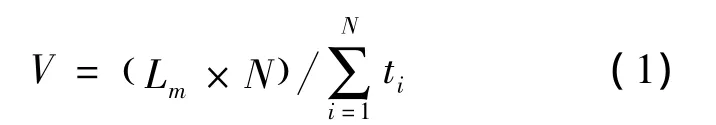
式中:Lm为路段的长度;N为路段在调查时间里的小时交通量;ti为调查时间里通过路段的第i辆车所需的行程时间。平均行程速度考虑了可能产生的停车延误,能更好地体现车辆在特定路段、特定时间的运行状态,是反映道路通畅程度的综合指标。
1.1.2 时间占有率
时间占有率O为在一定的观测时间内,交通检测器被车辆占用的时间与观测总时间的比值,
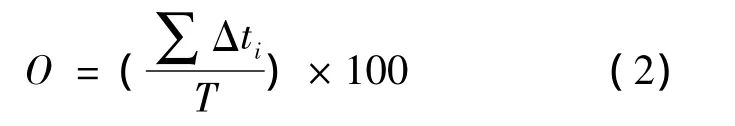
式中:Δti为第i辆车占用检测器的时间;T为观测总时间。时间占有率能体现交通流的运行状态。
1.2 交叉口评价指标的选取
1.2.1 饱和度
饱和度S为交叉口实际交通量与通行能力之比,

式中:V为进口车道的实际交通量;C为进口车道的通行能力。饱和度是反映交叉口总体拥挤程度和利用程度的综合指标。
1.2.2 每车平均延误
每车平均延误D为高峰时期所有车辆在交叉口延误段长度内实际行驶时间与在该段路长度内按畅行速度行驶时间之差的平均值,其计算模型为[8]
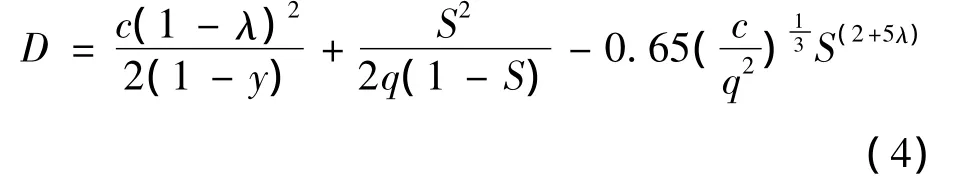
式中:c为信号周期时长;λ为绿信比;y是流入交通量与饱和交通量的比值,也称为流量比率;q为流入交通量;S为饱和度。每车平均延误表征车辆在通过交叉口的过程中所损失的时间,能比较直观地反映交叉口的通行情况和服务水平。
1.2.3 平均最大排队长度
平均最大排队长度L为各周期最大排队长度的平均值,其计算模型为[9]:

式中:Li为第i周期的最大排队长度;qi为第i周期的车辆到达流率;tr为红灯时长;β为到达分布系数,通常取2.0;S为饱和度。排队长度是交叉口一个非常重要的控制参数和评价参数,也是衡量交通拥堵最直观的指标。
2 模型的建立
2.1 建立评判因素集和判断集
因素集 U={u1,u2,…,un},表示被评判对象的各因素组成的集合。根据评价指标体系,道路交通状态的因素集为 U={V,O,S,D,L}。
判断集 F={f1,f2,…,fn},表示对被评判对象的所有评语组成的集合。根据对城市道路交通状态的划分,建立判断集 F={f1,f2,f3,f4}={畅通、缓行、拥挤、堵塞}。
2.2 建立各评价指标的隶属函数
常见的模糊集的隶属函数主要有三角形隶属函数、矩形隶属函数、梯形隶属函数、高斯型隶属函数等。本文选用控制特性平缓、分辨率高、稳定性也较好的梯形隶属函数,再根据海量的历史统计数据和专家经验来建立各个评价指标的隶属函数。
2.2.1 平均行程速度的隶属函数
参考我国公安部制定的《城市道路交通管理评价指标体系》(2008年版),根据其中的平均车速分级表(表1)确定平均行程速度对应于各种状态的阈值。
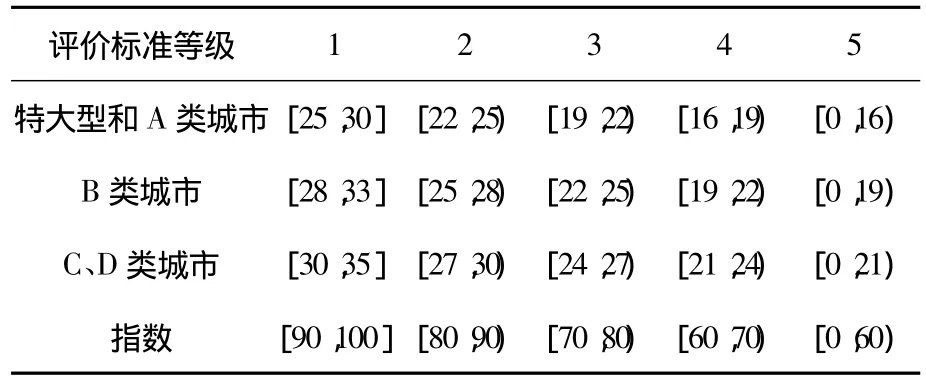
表1 高峰时段建成区主干道平均车速分级 km·h-1
本文所指道路为大城市的主干道,所以定义:平均行程速度V>25为畅通状态;V∈[21,24)为缓行状态;V∈[17,20)为拥挤状态;V<16为堵塞状态。隶属函数如图1所示。
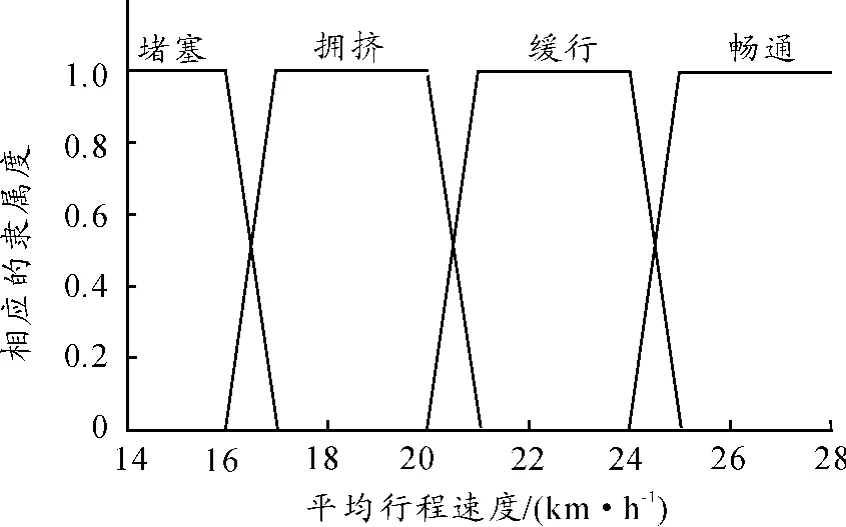
图1 平均行程速度的隶属函数
2.2.2 时间占有率的隶属函数
结合相关研究[10],定义:时间占有率O<5为畅通状态;O∈[10,15)为缓行状态;O∈[20,25)为拥挤状态;O>30为堵塞状态。隶属函数如图2所示。
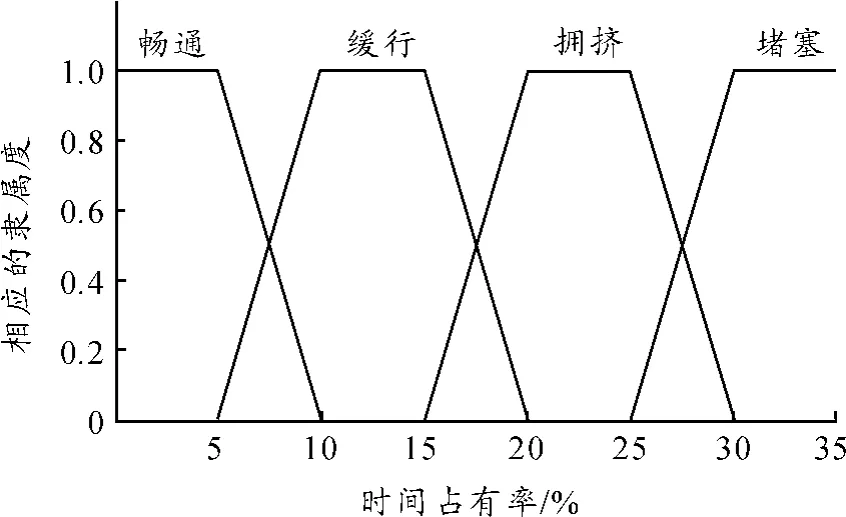
图2 时间占有率的隶属函数
2.2.3 饱和度的隶属函数
根据文献[9]中我国信号交叉口建议的服务水平分级标准(表2)确定饱和度对应于各种状态的阈值。

表2 我国信号交叉口建议的服务水平分级标准
定义:饱和度 S<0.5为畅通状态;S∈[0.6,0.7)为缓行状态;S∈[0.8,0.9)为拥挤状态;S >1.0为堵塞状态。隶属函数如图3所示。
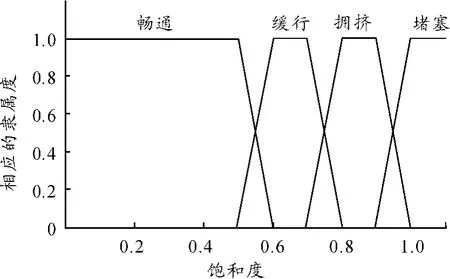
图3 饱和度的隶属函数
2.2.4 每车平均延误的隶属函数
根据表2中与延误时间指标相对应的服务水平分级标准确定每车平均延误对应于各种状态的阈值。定义:每车平均延误D<25为畅通状态;D∈[30,40)为缓行状态;D∈[45,55)为拥挤状态;D>60为堵塞状态。隶属函数如图4所示。
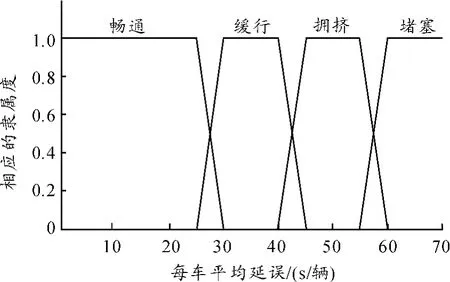
图4 每车平均延误的隶属函数
2.2.5 平均最大排队长度的隶属函数
根据表2中与排队长度指标相对应的服务水平分级标准确定平均最大排队长度对应于各种状态的阈值。定义:平均最大排队长度L<30为畅通状态;L∈[40,60)为缓行状态;L∈[70,90)为拥挤状态;L>100为堵塞状态。隶属函数如图5所示。
2.3 计算各评价指标的权重
评价指标的权重通常是由专家法或层次分析法来确定,但是专家法具有较大的主观性,层次分析法中检验和调整判断矩阵的一致性难度大,且判别标准CR<0.1缺乏科学依据,因此,本文采用克服了层次分析法中诸多缺点和局限的FAHP来计算各评价指标的权重。
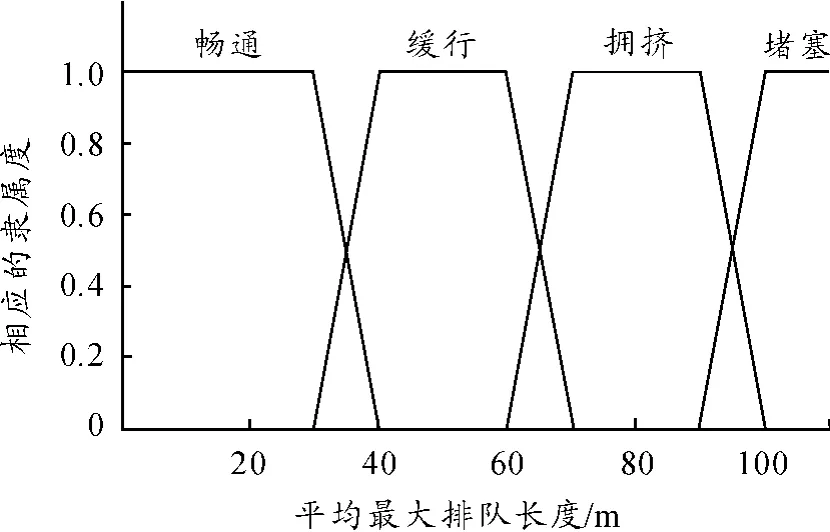
图5 平均最大排队长度的隶属函数
2.3.1 建立模糊互补矩阵
首先,引入模糊矩阵、模糊互补矩阵和模糊一致矩阵的定义[11]。若矩阵 A=(aij)n×n满足 0≤aij≤1,i,j=1,2,…,n,则称 A 是模糊矩阵。若模糊矩阵 A=(aij)n×n满足 aij+aji=1,i,j=1,2,…,n,则称 A是模糊互补矩阵。若模糊矩阵 A=(aij)n×n对任意 i,j,k 有 aij=aik- ajk+0.5 成立,则称A是模糊一致矩阵。
采用0.1~0.9数量标度法对影响同一目标的各因素之间的重要程度进行比较,综合数位专家的经验可得各评价指标对上层目标的模糊互补矩阵为
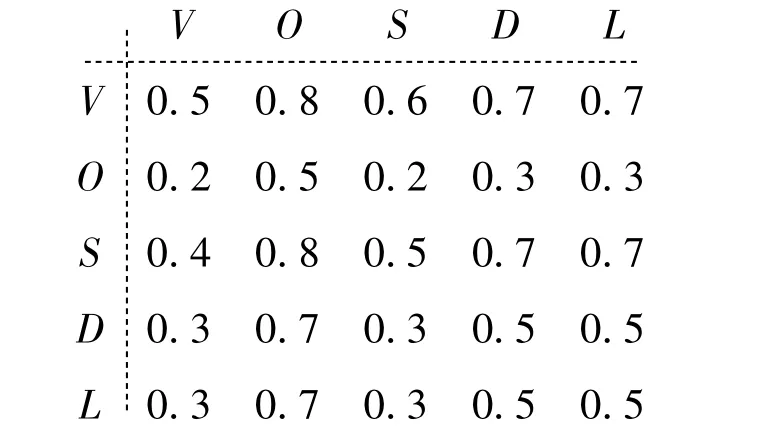
2.3.2 转化为模糊一致矩阵
首先对模糊互补矩阵A=(aij)n×n按行求和,并令,然后作变换:rij=,即可得到模糊一致矩阵R=(rij)n×n。于是将上面的模糊互补矩阵转化为模糊一致矩阵:

2.3.3 计算权重向量
由模糊一致矩阵A=(aij)n×n可得各指标对上层目标的权重
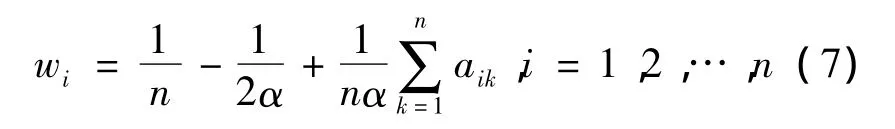
式中 α 是满足 aij= α(wi-wj)+0.5,i,j=1,2,…,n和的参数,它可以度量因素间权重的区分度。当α越大时,(wi-wj)就越小,因素间权重的区分度就越小;反之,因素间权重的区分度就越大。因此,决策者可以选择不同的α值并计算出对应的权重向量,然后根据决策的需要和专家经验选出最合适的权重向量。这里分别取α=2,α=2.5,α=3对上面的模糊一致矩阵计算出对应的3组权重向量。当α=2时,指标间相对重要程度的分辨率最高,且所得权重向量更符合实际情况,因此选择α=2时的权重向量,如表3所示。
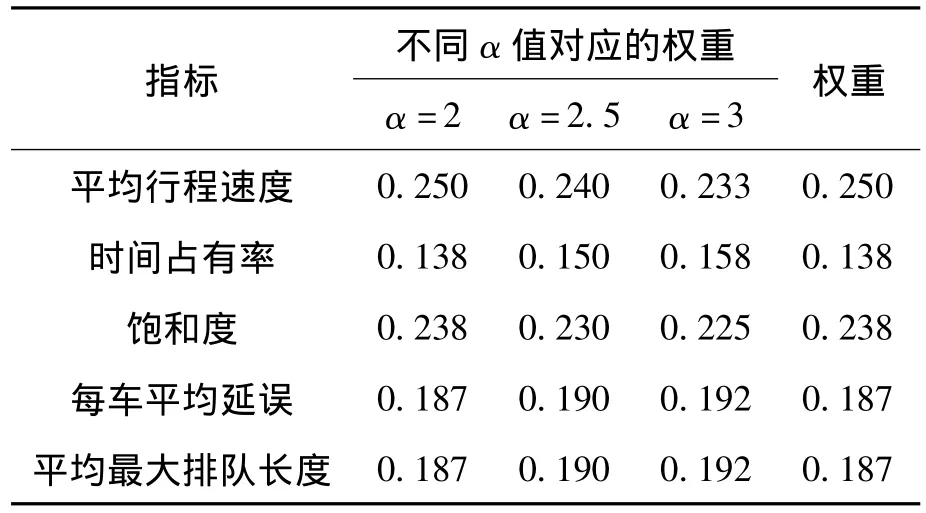
表3 权重
2.4 单因素判断
单因素判断就是对因素集中的单个因素的评判,得到判断集 F 上的模糊集(ri1,ri2,ri3,ri4)。其中 rij(j=1,2,3,4)表示因素 ui(i=1,2,3,4,5)对判断集中的 fj(j=1,2,3,4)的隶属度,所以它是从U到F的一个模糊映射。
对各评价指标进行单因素评判。每个指标都可以得到判断集F上的一个模糊集,从而由模糊映射可以确定模糊关系矩阵R,称为评判矩阵,它是由所有对单因素评判的模糊集组成。

其中 vi、oi、si、di、li(i=1,2,3,4)分别表示平均行程速度、时间占有率、饱和度、每车平均延误和平均最大排队长度对判断集中的fi(i=1,2,3,4)的隶属度。
2.5 模糊综合评判
对道路交通状态作模糊综合评判。将权重向量W与单因素评判矩阵R用模糊运算合成,得到综合评判集 A,其元素 ai(i=1,2,3,4)表示待评城市道路的交通状态属于评价等级fi(i=1,2,3,4)的隶属度。
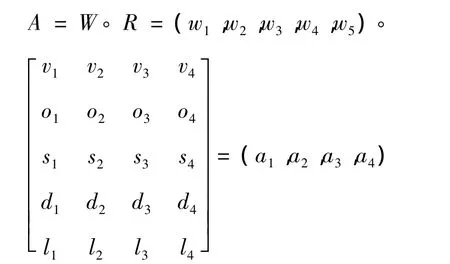
这里采用的模糊运算是实数的加乘运算,因为在进行模糊综合评判时,实数的加乘运算比“∨,∧”运算更精细,且得到的综合评判集具有归一性。
2.6 确定评判结果
确定评判结果的常用方法是最大隶属度原则,但该原则只突出主要因素,缺乏全面考虑。本文采用既突出主要因素又兼顾其他信息的加权平均法,该方法的权系数可根据设计要求和经验来选取。这里取综合评判集A的元素ai作为权系数。设判断集{f1,f2,f3,f4}={1,2,3,4},则根据平均加权法有
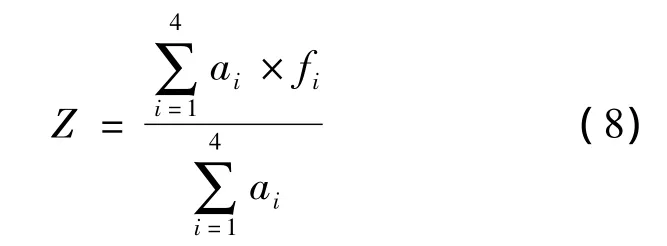
其中Z表示综合考虑所有因素的影响时待评城市道路交通状态的最终评判得分。定义它为交通状态综合指数,该指数表明交通状态的变化过程是连续的,而不是由一个状态立刻变到另一个状态,这使模型更加合理。
3 仿真验证
本文建立模拟道路如图6所示,其中交叉口的东西南北方向都是双向6车道,西—东路段长490 m。以西—东路段和交叉口为分析对象,采用VISSIM 4.3建立仿真道路,得到的交通仿真过程如图7所示。
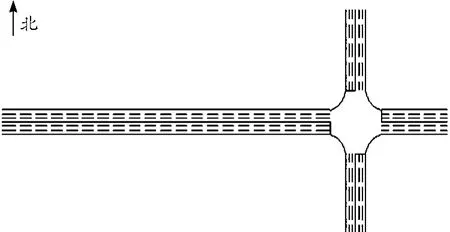
图6 模拟道路
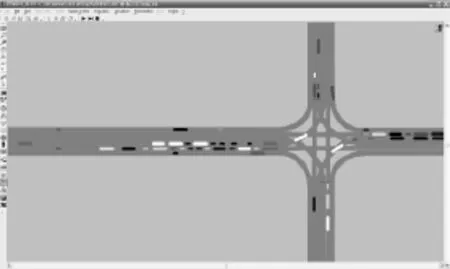
图7 交通仿真过程
通过在不同时段输入不同的交通流量来验证判别模型在不同交通状态下的判别效果。仿真总时间为6 000 s,每隔5 min采集一次数据,将得到的模拟数据进行处理,计算各评价指标的值,得到各时段的交通状态综合指数如图8所示。
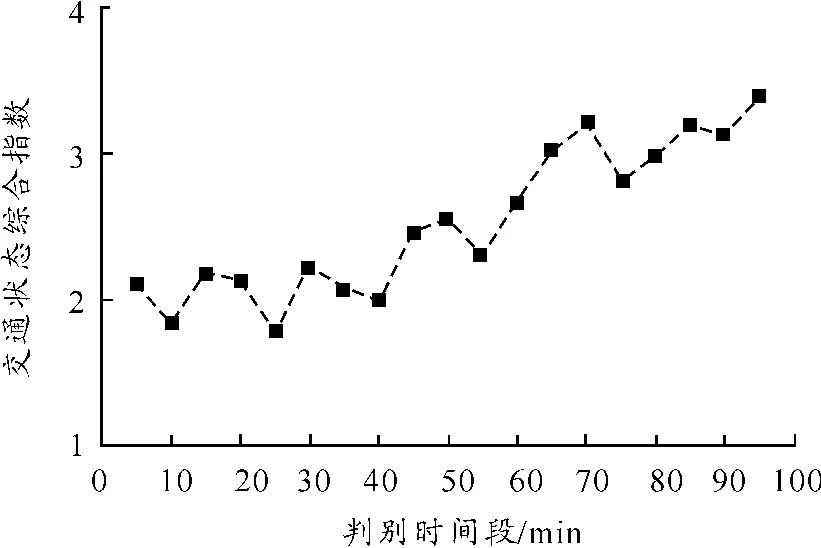
图8 判别效果
由图8可知,模型的判别结果比较稳定,交通状态的变化是连续渐变的。模拟道路有较长时间处于缓行和拥挤状态,与仿真交通状况相符。
4 结束语
以FAHP和模糊综合评判为核心方法,针对5个主要的交通流参数,建立了一种道路交通状态判别模型。通过仿真验证,可知该模型很好地体现了交通状态是连续渐变的性质,切实地与人们对交通运行状况的感受相联系,从而更有效地判别道路交通状态。因此,模型为准确地分析道路运行情况和缓解交通拥堵提供了一种新的、有效的方法。
[1]Vaziri M.Development of Highway Congestion Index with Fuzzy Set Models[J].Journal of Transportation Research Record 1802,Transportation Research Board,2002:16-22.
[2]祝付玲.城市道路交通拥堵评价指标体系研究[D].南京:东南大学,2006.
[3]Liu M,Yu L,Guo J.Fuzzy Logic-based Urban Traffic Congestion Evaluation Models and Applications[C]//The First International Conference on Transportation Engineering.China:[s.n.],2007:22 -24.
[4]张毅媚,黄进堂.基于模糊数学的交通拥挤评价指标[J].华中科技大学学报:城市科学版,2008,25(1):65-68.
[5]任其亮,肖裕民.城市路网交通拥堵H-Fuzzy评判方法研究[J].重庆交通大学学报:自然科学版,2008,27(5):763-766.
[6]冷欢平.城市路网交通状态评价研究[D].长春:吉林大学,2008.
[7]戢晓峰,刘澜,何增辉.基于模糊推理的区域路网交通状态分析方法[J].交通运输工程与信息学报,2009,7(3):27-32.
[8]饭田恭敬.交通工程学[M].北京:人民交通出版社,1993:239-244.
[9]任福田,刘晓明,荣建,等.交通工程学[M].北京:人民交通出版社,2003:187-190.
[10]曹成涛,崔凤,林晓辉.基于神经网络的交通状态模糊判别方法[J].科学技术与工程,2010,10(21):5195-5199.
[11]张吉军.模糊互补判断矩阵排序的一种新方法[J].运筹与管理,2005,14(2):59 -63.

