汽车运行工况域动态调节仿真
陈渝光,边晓彬,吕红梅,周 桐
(重庆理工大学 a.汽车零部件制造与检测技术教育部重点实验室;b.电子信息与自动化学院,重庆 400054)
汽车在复杂路面上行驶时,发动机工况在相当大的范围内是处于经常而急促的变化中,这对发动机性能将产生较明显的影响[1]。目前,工况判断主要依据台架实验数据,显然,这种判断方法并不能反映汽车在复杂运行条件下的真实运行工况。例如,当汽车在较差的路面上运行时,虽然发动机转速与负荷变化相当大,但汽车在一定时间周期内的工况特征可能是相对稳定的,如果按现有的工况确定方法去设定发动机的控制参数,将对发动机动力性、燃油经济性和排放性能产生不利影响,具有较大的局限性和较差的适应能力。
基于上述问题,引入了运行工况和运行工况域的概念。运行工况是指发动机在实际运行过程中存在的工作状况,采用转速n和负荷L来表征。运行工况域是指在实际运行条件下,发动机稳定运行工况允许的波动范围。汽车在复杂路面上运行时,基于免疫神经网络动态调节发动机的运行工况域,可以明显改善发动机动力性、燃油经济性和加减速性能[2]。本文运用Matlab/Simulink对发动机在复杂路面上行驶时的运行工况域动态调节进行仿真研究。
1 汽车运行工况域动态调节
1.1 运行工况模糊判断
设:
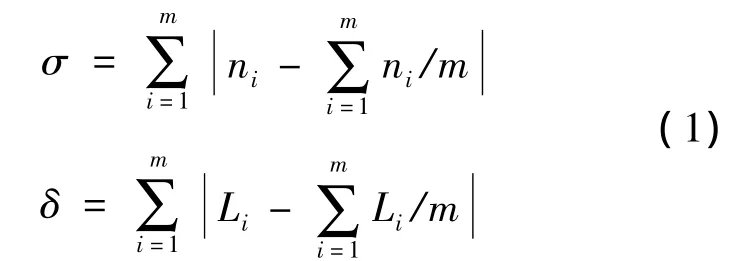
式中:ni为发动机转速采样值;Li为发动机负荷采样值;m为采样周期内的采样次数。
当σ=0时,为转速稳定工况;当δ=0时,为负荷稳定工况。采用隶属度函数μA()σ=e-K1σ2、μB()δ=e-K2δ2分别描述σ、δ隶属于转速稳定工况、负荷稳定工况的程度[3]。K1、K2决定隶属函数曲线的形状,依据发动机参数和运行工况域确定。
设Δni大于零的各项为Δni+,小于零的各项为 Δni-;ΔLi大于零的各项为 ΔLi+,小于零的各项为 ΔLi-。则:
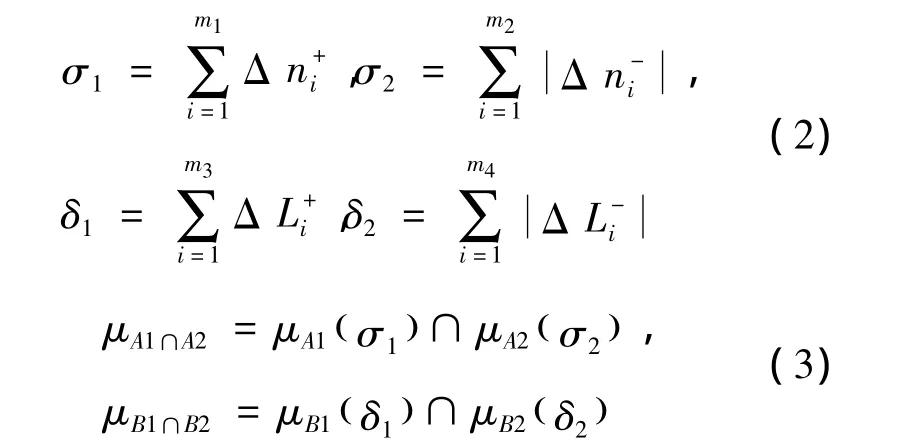
根据μA(σ1)和μA(σ2)的大小关系可以判断发动机加减速工况。同时,由式(3)还可以判断转速和负荷的加减速变化趋势。
1.2 运行工况域确定
以转速运行工况域确定为例,负荷运行工况域确定与转速运行工况域的确定方法类似。实验环境:Vela 1.5AT型轿车发动机台架试验,n=(1 500±0.5)r/min。实验结果:发动机每10 r/min中转速波动为(±1.0)r/min,K1=0.01 时,μA(σ)=0.88;转速每10 r/min 中转速波动(±1.5)r/min,K1=0.005 时,μA(σ)=0.88。
因此,将μA(σ)=0.88作为转速运行工况域边界的判断条件。μA(σ)≥0.88属于转速稳定工况,反之,μA(σ)<0.88属于转速不稳定工况。
当K1在0.01~0.005调节时,转速运行工况域也随之动态调节,其每10 r/min转速在允许波动范围(±1~±1.5)r/min内动态调节。因此,可以根据路面不同,通过调节K1值调整隶属函数曲线形状,从而达到动态调节转速运行工况域的目的。
1.3 运行工况域动态调节
发动机运行工况域动态调节框图如图1所示。
为了便于动态调节,令K1=0.01×(1-α1),K2=0.01 ×(1 - α2),0≤α1、α2≤0.5,这里,α1、α2分别代表 K1、K2的免疫调节因子。免疫控制器[4-6]通过调节 α1、α2动态调节 K1、K2,从而达到动态调节运行工况域的目的。

其中 f[Δu(k)]=1 -exp[-(1 -uA(k))2/0.1]。刺激因子N1、抑制因子N2由BP神经网络进行在线调节,分别控制响应速度和稳定性。
α2的免疫动态调节方法与α1相同。
2 运行工况域动态调节仿真
2.1 BP 神经网络
BP神经网络由输入层、隐含层和输出层组成。下面以转速运行工况域动态调节的BP神经网络为例。输入层神经元个数为3,分别为dn/dt、1-μA和d(1-μA)/dt。输出层神经元个数为2,分别为N1和N2。隐含层神经元的激活函数取正负对称的Sigmoid函数,输出层神经元的激活函数取非负的Sigmoid函数。初始值选取较小的随机数。
由黄金分割原理和神经网络训练的总误差确定隐含层神经元数。经过81次循环,网络收敛,训练误差 E(12)=3.27769e-030,由此确定的隐含层神经元数为12。提取相应的权值和阈值,并在Matlab/Simulink环境中建立神经网络模型。
2.2 运行工况域动态调节仿真模型
下面以转速运行工况域动态调节仿真为例。负荷运行工况域动态调节的仿真方法与转速运行工况域动态调节仿真类似。实际输入信号为转速偏差信号Δn,输出信号为隶属度函数μA。采样时间T=0.05 s,采样周期内的采样次数m=5。转速运行工况域动态调节仿真模型如图2所示。图2中,Subsystem为 BP神经网络模块,Embedded Matlab Function为计算 μA(σ)的模块;Fcn3、Product和Product1为免疫调节模块;Fcn模块的输出是K1。
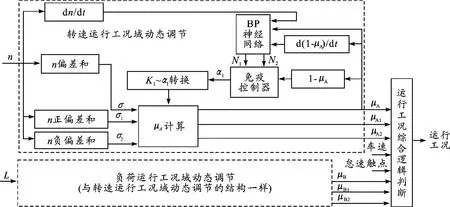
图1 发动机运行工况域动态调节框图
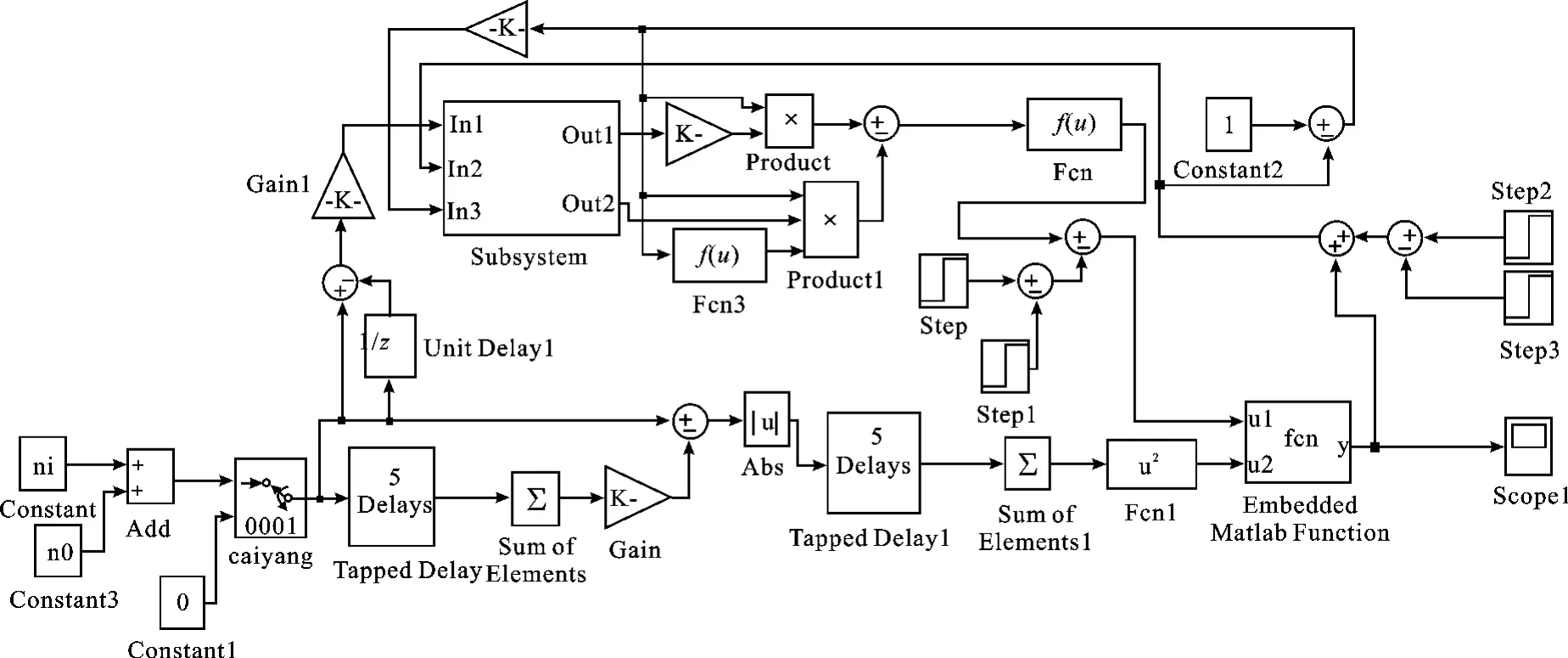
图2 转速运行工况域动态调节仿真模型
2.3 仿真模型验证
当 Δn=1.158sin(2πt)时,K1、μA(σ)波形如图3、图4所示。由图3和图4可看出,当 K1在0.005~0.01 动态调节时,μA(σ)≥0.88。这证明了所建立仿真模型的正确性以及动态调节方法和动态调节范围的准确性。
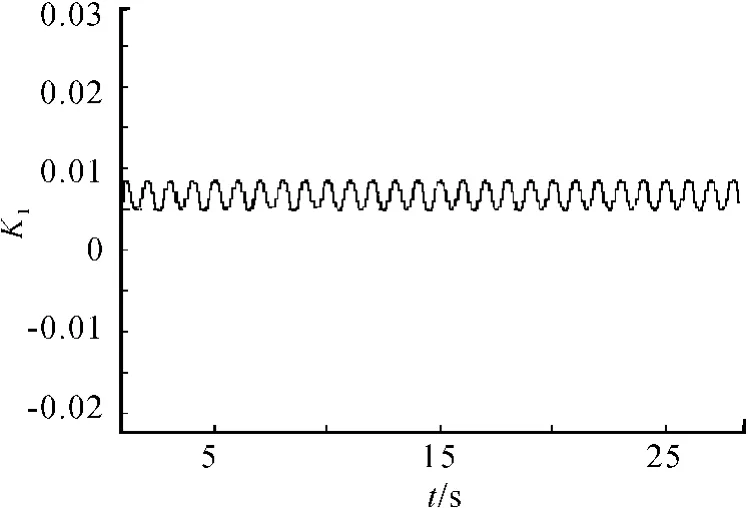
图3 Δn=1.158sin(2πt)时的 K1
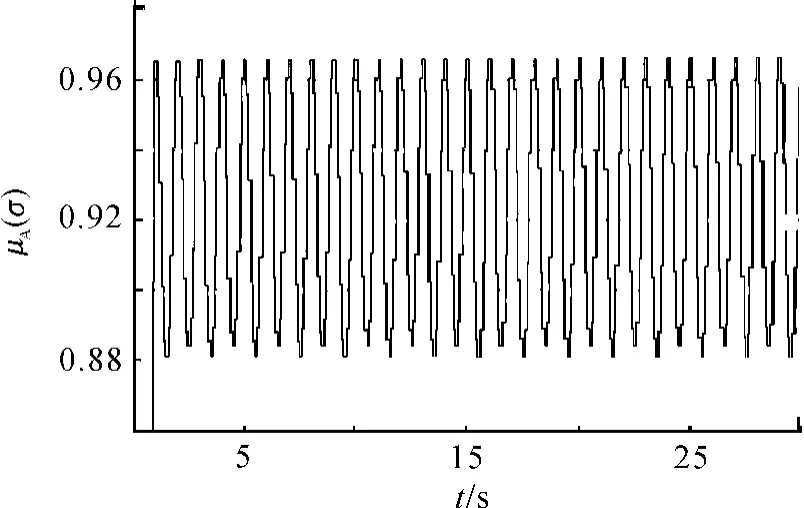
图4 Δn=1.158sin(2πt)时的 μA(σ)
2.4 运行工况域动态调节仿真
Δn分别采用正弦和随机2种典型信号。正弦信号可以达到理想模拟转速、负荷周期变化的幅值与频率;随机输入信号符合实际路面的变化情况。
当 Δn=1.282sin(πt),K1在 0.005 ~0.01 动态调节时,μA(σ)≥0.88,转速处于稳定运行工况。K1、μA(σ)值的动态调节波形如图5、图6所示。
当Δn为随机信号,初始“种子”为0,幅值为1.18,K1在 0.005 ~0.01 动态调节时,μA(σ)≥0.88,转速处于稳定运行工况。K1、μA(σ)值的动态调节波形如图7、图8所示。
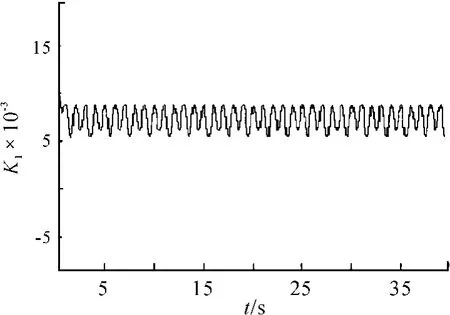
图5 Δn=1.282sin(πt)时的 K1
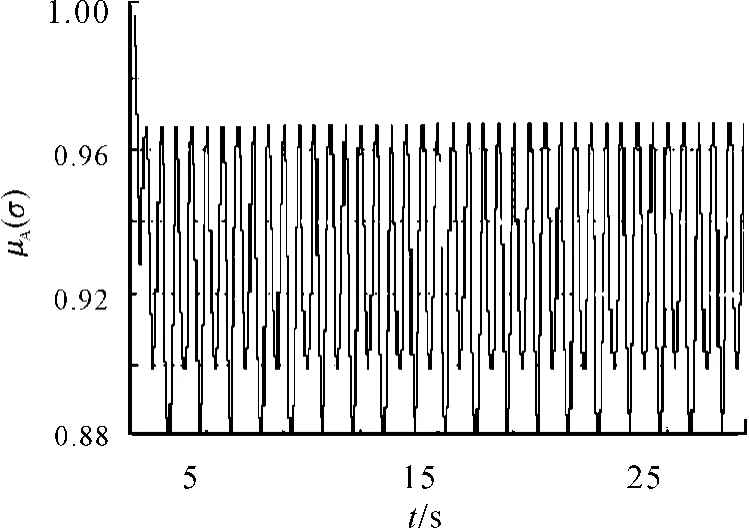
图6 Δn=1.282sin(πt)时的 μA(σ)
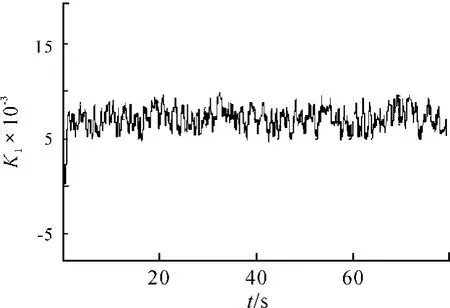
图7 Δn为随机信号时的K1
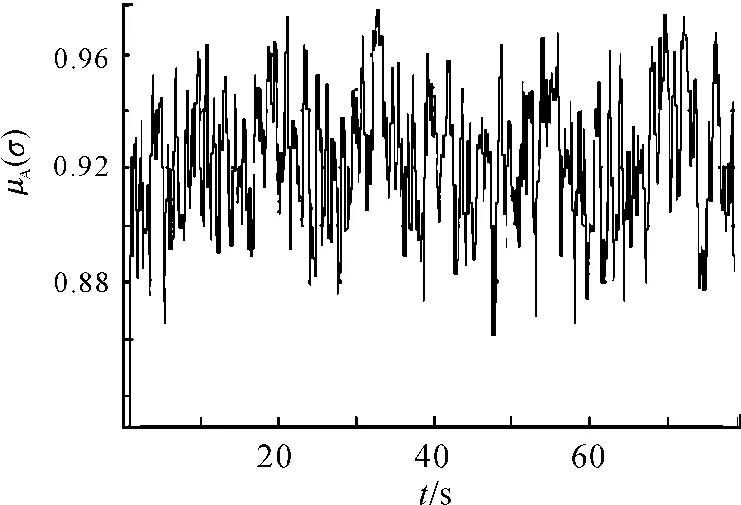
图8 Δn为随机信号时的μA(σ)
在所定义的区间内,随机函数具有均匀性和独立性。采用20种不同初始“种子”的随机输入进行仿真,在满足μA(σ)≥0.88的前提下,其随机信号的幅值如表1所示。

表1 不同的随机函数序列得到幅值
运用均值算法得到的幅值为1.154 5。说明当转速偏差信号为随机信号时,发动机运行于稳定运行工况允许的平均转速波动幅值为1.154 5。
3 仿真结果分析
对转速运行工况域动态调节进行仿真分析,可以得到以下结论:
1)由图3~8可看出:随转速变化,K1在0.005~0.01 动态调节时,μA(σ)≥0.88,转速处于稳定运行工况。也就是说,虽然转速频率和幅值在一定的范围内快速变化,转速运行工况域也在随之动态调节,转速运行工况仍然属于稳定状态。转速运行工况域的动态调节,使发动机能适应在复杂路面上运行的工况。
2)从 Δn 分别为1.158sin(2πt)和1.282sin(πt)的仿真结果可以看出:当Δn周期不变,随Δn幅值增加时,μA(σ)下降;当 Δn幅值不变,随 Δn周期增加时,μA(σ)下降。也就是说,转速运行工况与Δn幅值和周期密切相关,克服了对转速变化率的敏感性。
传统转速工况判断方法依据dn/dt≦ε,它对转速变化率非常敏感。因此,本文所述运行工况域的判断方法,更能真实反映发动机在较复杂路面上运行的工况。
3)适当增大K1的调节范围,可以增大运行工况域的动态调节范围,更有利于发动机在复杂路面上运行。
4 结束语
在发动机工况模糊判断的基础上,利用免疫神经网络分别在线调节 α1、α2来调节 K1、K2,从而通过调整隶属函数曲线形状达到动态调节运行工况域的目的。Matlab/Simulink仿真实验表明,基于免疫神经网络的运行工况域动态调节方法克服了对转速变化率的敏感性,更能真实反映发动机运行工况。适当增大K1、K2的调节范围,可以增大运行工况域的动态调节范围,更有利于发动机在复杂路面上运行。
[1]刘希玲,丁焰.我国城市汽车运行工况调查研究[J].环境科学研究,2000,13(1):24 -27.
[2]陈渝光,冯学敏,于淼,等.基于免疫原理的发动机工况参数负荷的多模态测量[J].武汉理工大学学报,2009,31(6):104 -108.
[3]林其明,杨胜国,朱从乔,等.基于模糊识别的柴油机下况判断[J].柴油机设计与制造,2003(3):13-17.
[4]Naira Hovakimyan,Flavio Nardi,Nakw an Kim,et al.A-daptive Output Feedback Control of Uncertain Systems U-sing Single Hidden Layer Neural Networks[J].IEEE Transactions on Neural Networks,2002,13(6):1420-1431.
[5]Kim D H.Tuning of a PID controller using immune network mode1 and fuzzy set[A].Industrial Electronics,2001 Proceedings[C]//ISIE2001.IEEE International Symposium on 2001.USA:[s.n.],2001:1656 -1661.
[6]Takahashi K,Yamada T.Application of an Immune feedback mechanism to control system[J].JSME International Journal,1998,41(2c):125 -127.
[7]石来华,冯仁华.基于GT-POWER模型的发动机进气系统优化[J].客车技术与研究,2010(3):18-21.

