改进孪生支持向量机的一种快速分类算法

高斌斌，刘 霞，李秋林

(1.西南大学数学与统计学院，重庆 400715;

2.新疆大学数学与系统科学学院，乌鲁木齐 830046)

支持向量机 (support vector machine，SVM)［1－10］是Vapnik等提出的一种基于统计学习理论的机器学习方法，能非常成功地处理分类和回归问题。由于它采用结构风险最小化的原则［11］而具有良好的学习能力和泛化性能，因此得到广泛应用(如图像识别、文本分类、生物信息、金融应用)。尽管许多快速 SVM算法(如 Chunking、分块、SMO和Liblinear等［12］算法)已被相继提出，但在实际应用中面对大规模数据，分类算法需要进行大量的二次规划计算，分类计算量大、分类速度慢，速度问题在很大程度上限制了SVM的应用。

2007年，Jayadeva等［13］提出了孪生支持向量机(TSVM)。该算法优化目标要求超平面离本类样本尽可能的近，离它类样本尽可能的远。TSVM计算时间开销缩减到SVM的1/4。然而，奇异性问题导致TSVM不能保证得到较好的分类性能。基于TSVM思想，近年来发展了许多有关非平行的超平面学习方法，如光滑 TSVM［14］、最小二乘TSVM［15］、TBSVM［16］。最近，彭［17］提出了 TPMSVM，该模型通过正、负参数间隔超平面间接确定分类最优超平面。

为了更好地提高TSVM算法的学习速度和泛化能力，提出改进的TSVM(ITSVM)模型，并将收缩技术［18］嵌入坐标下降方法［19］求解改进模型，十分有效地改善了TSVM的学习速度和分类能力。仿真实验表明:相对于传统的SVM、TSVM及TPMSVM方法，ITSVM不仅提高了分类的准确率，而且大大改善了计算效率。

1 改进的孪生支持向量机

给定 2类 n维的 m个训练样本，T={(xi，yi)}，xi∈Rn，对于二分类问题，yi={+1，－1}(i=1，…，m)作为类别的标签。分别用m1×n的矩阵X+和m2×n的矩阵X－表示为+1类和－1类，m1、m2分别表示2类样本的数目。

1.1 改进的线性孪生支持向量机

考虑到现有的孪生模型并不具有类似于SVM的特性，即间隔［20］，基于SVM结构风险最小化和最大间隔原则，在TSVM模型原始优化问题中添加正则项，使得构造的优化问题的优化目标结构风险最小，从而提高TSVM的泛化性能。线性情形下，ITSVM也是寻找2个不平行的超平面:

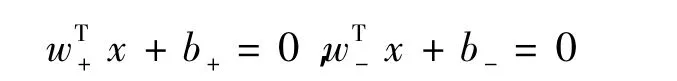
为了获得这2个超平面，改进后的原始问题为:

其中:εi＞0(i=1，2)是正则化参数;ci＞0(i=1，2)是惩罚参数。

显然，最优超平面wT±x+b±=0与边界超平面wT±x+b±= ±1 之间的间隔是，因此目标函数极小化正则项和与极大化间隔等价，也就是使得最优超平面与边界超平面的距离尽可能的远。原始问题(2)的Lagrangian函数为

其中 α =(α1，α2，…，αm2)T是 Lagrange乘子。根据The Karush Kuhn Tucker(KKT)条件:

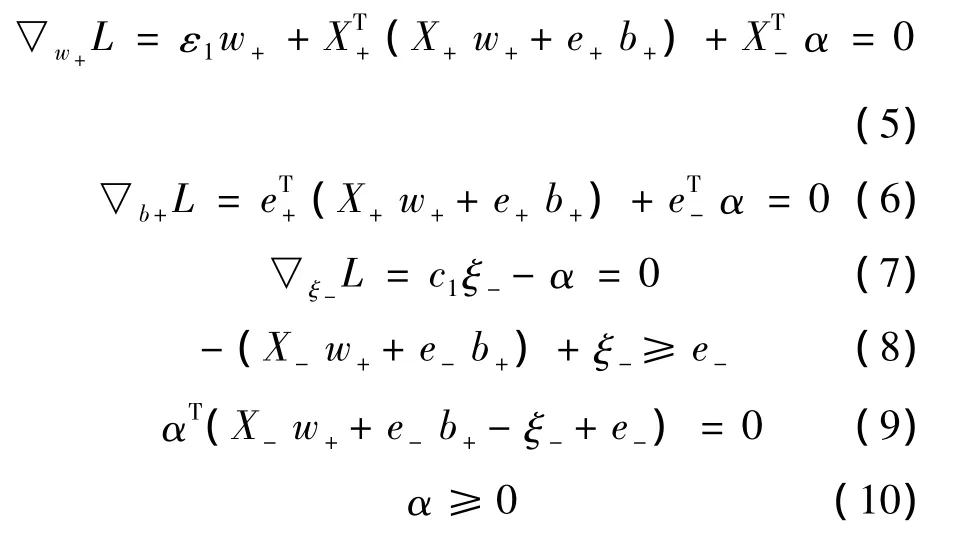
合并式 (5)、(6)可以得

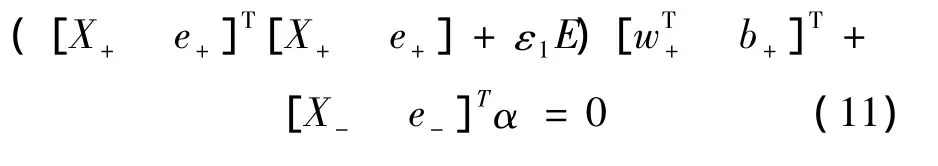
职业教育是国家教育事业的重要组成部分，是促进经济社会发展和劳动就业的重要途径。在新时代，职业教育更是被赋予培养“大国工匠”的历史重任，写入了党的十九大报告，纳入重庆科教兴市和人才强市行动计划，其重要性不言而喻。发展是第一要务，人才是第一资源。在新一轮改革发展浪潮中，如何通过加快区县职业教育发展，推动人才与发展有效匹配、教育与产业紧密对接、科技与经济深度融合，助推实现“两地”“两高”目标，值得研究和探索。

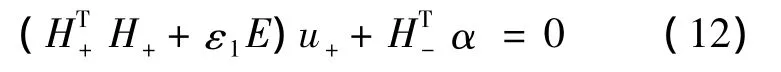
由式(12)得

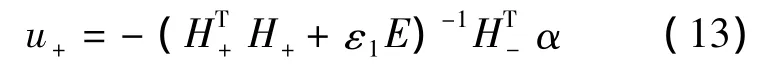
将式(13)带入Lagrangian函数(4)，使用约束条件(7)～(10)，可以得到问题(2)的Wolfe对偶问题:

类似的方式可以得到问题(3)的Wolfe对偶问题:

求解对偶问题(14)和(15)，得到Lagrange乘子α和β，从而得到权重向量w±和偏置值b±。对于一个新的输入x∈Rn是+1类还是－1类，可依据决策函数判别，其中是绝对值。

1.2 改进的非线性孪生支持向量机

对于线性不可分问题，引进从输入空间Rn到一个高维的Hilbert空间H的变换φ，这样在原空间寻找超平面的问题转化为在特征空间H中寻找2个由核生成超平面:

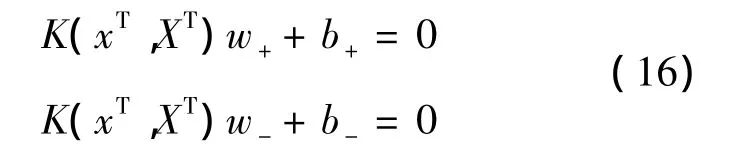
的问题，其中 K(x，y)=φ(x)Tφ(y)为核函数。为了将线性情况的结果拓展到非线性情况，构造原始优化问题

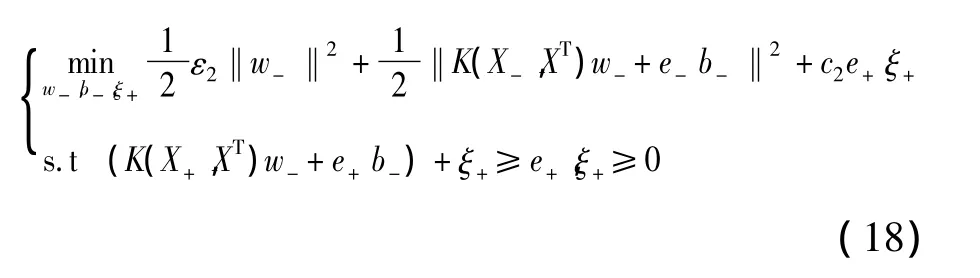
记 S+=［K(X+，XT)e+］，S－ =［K(X－，XT)e－］，引进Lagrangian函数，利用KKT条件，可以获得原始优化问题(17)和(18)的对偶问题:

2 ITSVM的快速求解算法

在ITSVM模型中，需求解对偶问题(14)、(15)、(19)和(20)。易知这4个问题都是凸二次规划问题，可以用同样的方法解决。因此只需要探究问题(14)的求解算法.

文献［19］将坐标下降法成功应用于求解SVM的对偶问题。问题(21)和SVM的对偶问题形式类似，但是却又不同，这是由于问题(21)与文献［19］的矩阵Q有本质的不同。收缩技术可以有效地处理非常大的数据集，该算法有效性已在文献［18］中得到证明。结合坐标下降算法与收缩技术的优势，得到了针对ITSVM对偶问题的高效求解算法。

算法的迭代过程由 α0∈Rm2开始，记 αk，1= αk，αk，m2+1= αk+1，且

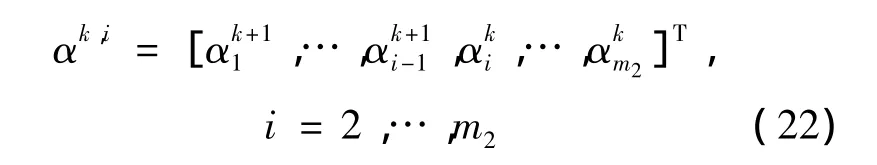
从 αk，i更新到 αk，i+1:

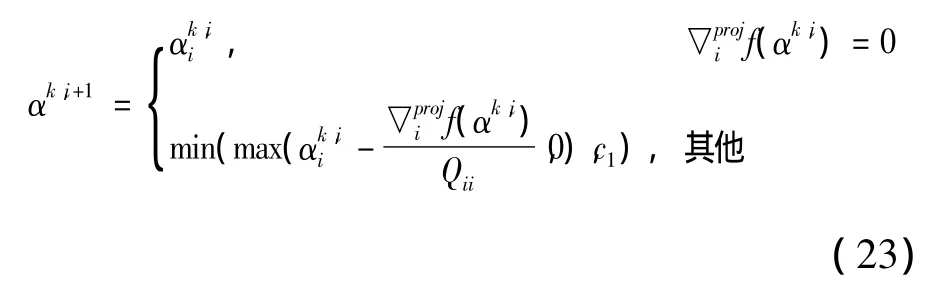
其中:

3 实验结果

为了验证ITSVM的分类性能，在人工数据与UCI数据集上对SVM、TSVM、TPSVM和ITSVM分别进行对比测试。实验运行环境:Windows7操作系统，CPU为 Intel corei3(2.4GHz)，内存为2G，Matlab 7.13软件。对所有方法的线性和非线性情形分别进行了测试。非线性情形下使用高斯核函数:K(x，y)=e－‖x－y‖2/(2σ2)。为了对比实验的执行效率，用本文提出的算法求解ITSVM，对SVM、TSVM 和 TPMSVM 使用“qp.m”函数求解［21］，分类准确率采用标准的十折交叉验证方法。

众所周知，参数对模型分类准确率有一定程度的影响，为了简化参数的搜索难度，在ITSVM中设置 ε1=ε2=ε，c1=c2=c，所有算法参数范围统一在集合{2i|i=－8，…，8}内，随机选择30%的训练集作调试集，通过网格搜索方法寻找最佳的参数。一旦参数被确定下来，调试集将还原到训练集中。

3.1 人工数据集实验

2 维数据 Ripley’s synathetic［22］常用于测试分类算法的性能，此数据有250个训练点，1 000个测试点。本节将通过此数据测试ITSVM与SVM、TSVM、TPMSVM在分类准确率与分类效率上的性能。在线性与非线性下分别通过训练集训练4种模型，然后对测试数据分别进行分类预测。记录预测的准确率和模型的训练时间如表1所示，4种方法的决策超平面如图1、2所示。

表1 4种算法在Ripley’s数据上的分类结果

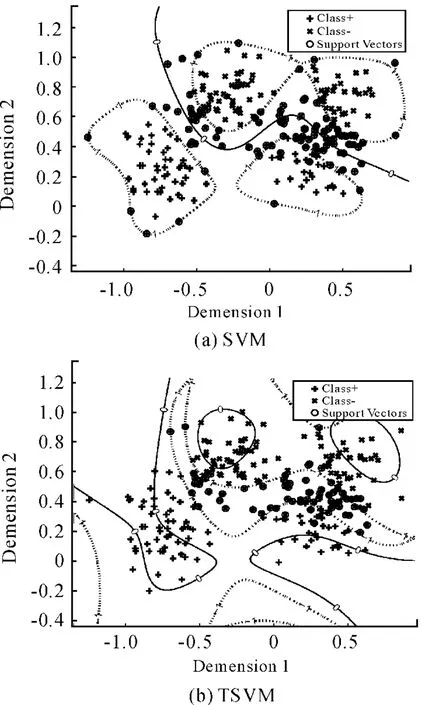
图1 非线性的SVM与TSVM分类超平面

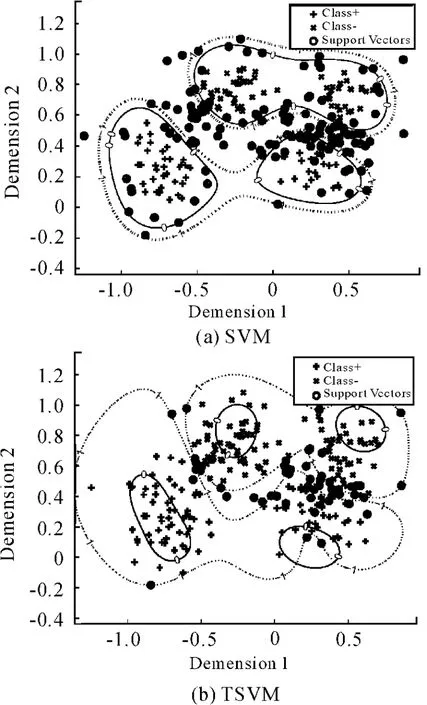
图2 非线性的TPMSVM与ITSVM分类超平面

从图1、2可以看出:经典SVM的决策边界是一个超平面，而TSVM、TPMSVM和ITSVM有2个超平面;ITSVM两条超曲线的位置相对TSVM、TPMSVM更加合理。

从表1结果可以知道:在测试准确率上，非线性的ITSVM获得了最佳的分类准确率，而在线性情形下传统的SVM获得了最佳的分类准确率;在算法的执行效率上，本文提出的方法相对于已有的SVM、FSVM、TSVM方法具有明显的优势，尤其是在线性情形下算法的执行效率表现得更为出色。

3.2 真实数据集实验

为了进一步测试ITSVM算法的有效性和实用性，在公开的UCI机器学习数据集［23］上选取了8个常用的数据，同相关方法SVM、TSVM、TPMSVM做对比实验，以更全面说明本文算法的分类性能。

数据集中同时包括二分类和多分类数据。对于多分类数据，处理方法是把类别数量比例较高的作为+1类，其余的作为－1类，从而转化为二分类问题。在实验之前，为了减少样本的不同特征的数量差别，归一化所有的样本数据在区间［－1，1］。表2和表3显示了在线性和非线性情况下本文所提方法 ITSVM与SVM，TSVM及 TPMSVM方法在给定数据集上的模式分类精度和学习的CPU时间。

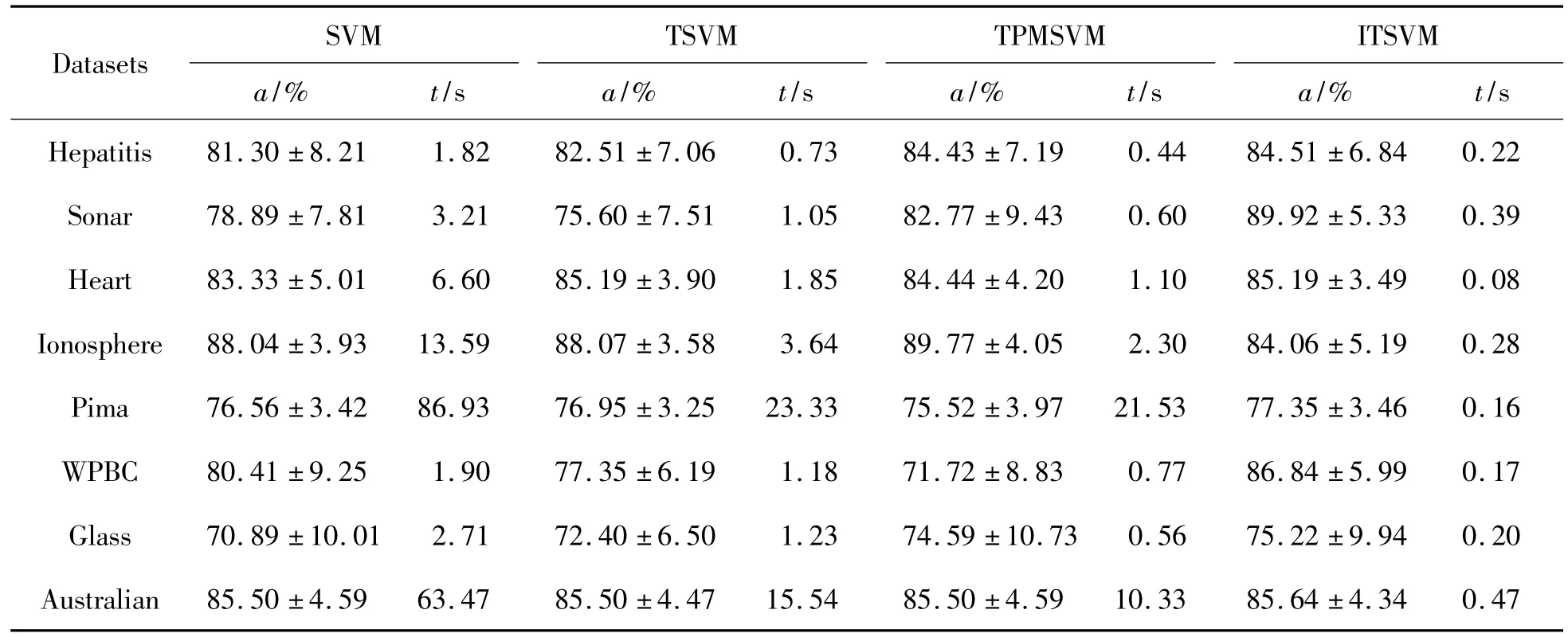
表2 线性SVM、TSVM、TPMSVM与ITSVM的分类结果

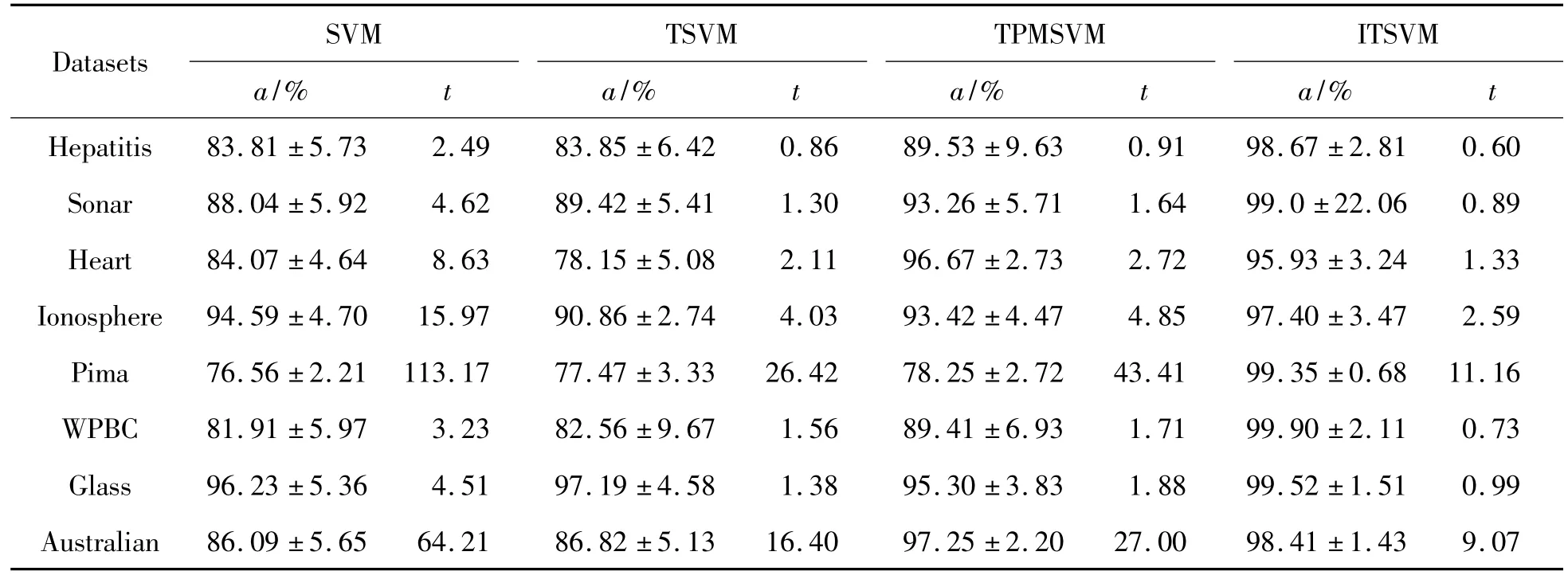
表3 非线性SVM、TSVM、TPMSVM与ITSVM的分类结果

由表2和表3可以得到:

1)采用非线性核能明显增强4种分类方法在几乎所有数据集上的分类性能。

2)无论是在线性情形还是非线性情形下，与已有方法SVM、TSVM及TPMSVM相比，ITSVM在绝大部分数据集上均具有优于其他方法的模式分类性能。

3)在算法的执行效率上，TSVM及 TPMSVM相对于SVM明显高效，但是本文提出的算法的分类速度表现更加出色，在线性情形下更具优势。

4 结束语

本文在TSVM的基础上，借鉴SVM结构风险最小化思想来构建原始优化问题，提出ITSVM分类模型。该模型的对偶问题为凸二次规划问题，可以得到全局唯一解。针对此模型，提出一种新颖的坐标下降算法，能有效地求解ITSVM的对偶问题。在人工数据与UCI数据集上测试证实:在线性和非线性情况下，本文方法ITSVM的分类准确率和执行效率优于或等于相关方法。但是，ITSVM模型中有4个参数需要确定，这增加了参数选择的难度。如何更好地选择参数，同时将此方法应用于多分类问题和回归问题，都是接下来要进行的研究工作。

［1］Cortes C，Vapnik V N.Support vector networks［J］.Machine Learning，1995，20(3):273 －297.

［2］余珺，郑先斌，张小海.基于多核优选的装备费用支持向量机预测法［J］.四川兵工学报，2011(6):118－119.

［3］万辉.一种基于最小二乘支持向量机的图像增强算法［J］.重庆理工大学学报:自然科学版，2011(6):53－57.

［4］王俊伟，吴纬.基于支持向量机的装备维修保障专业优化［J］.四川兵工学报，2010(6):11－13.

［5］邬啸，魏延，吴瑕.基于混合核函数的支持向量机［J］.重庆理工大学学报:自然科学版，2011(10):66－70.

［6］朱光兆，何伟.基于支持向量机的混沌时间序列预测分析［J］.自动化与仪器仪表，2012(1):145－147.

［7］张宏蕾，张立亭，罗亦泳，等.基于支持向量机的土地利用预警研究［J］.安徽农业科学，2010(35):20503－20504.

［8］黄银蓉，张绍德.MIMO最小二乘支持向量机污水处理在线软测量研究［J］.自动化与仪器仪表，2010(4):15－17.

［9］唐晓芬，赵秉新.基于支持向量机的农村劳动力转移预测［J］.安徽农业科学，2011(11):6837－6838.

［10］崔建国，李明，陈希成.基于支持向量机的飞行器健康诊断方法［J］.压电与声光，2009(2):266－269.

［11］cholköpf B S，Smola A.Learning with kernels［M］.Cambridge，MA:MIT Press，2002，62 －75.

［12］Fan R E，Chang K W，Hsieh C J，et al.LIBLINEAR:a library for large linear classification［J］.Journal of Machine Learning Research.2008，9:1871 －1874.

［13］Jayadeva R K，Khemchandani R，Chandra S.Twin support vector machines for pattern classification［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(5):905 －910.

［14］Kumar M A，Gopal M.Application of smooth in technique on twin support vector machines［J］.Pattern Recognition Letters，2008，29(13):1842 －1848.

［15］Kumar M A，Gopal M.Least squares twin support vector machines for pattern classication［J］.Expert Systems with Applications，2009，36(4):7535 －7543.

［16］Shao Y H，Zhang C H，Wang X B.Improvements on twin support vector machines［J］.IEEE Transactions on neural networks，2011，22(6):962 －968.

［17］Peng X J.TPMSVM:A novel twin parametric－margin support vector machine for pattern recognition［J］.Pattern Recognition，2011，44:2678 －2692.

［18］Hsieh C J，Chang K W，Lin C J.A dual coordinate descent method for large－scale linear SVM［C］//Proceedings of the 25th international conference on machine learning.USA:［s.n.］，2008.

［19］Joachims T.Making large－scale SVM learning practical［M］.Cambridge，MA:MIT Press，1998:169 －184.

［20］丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述［J］.电子科技大学学报，2011，40(1):2 －10.

［21］Gunn S R.2001 MATLAB support vector machine toolbox version:2.1［EB/OL］.［2011 －05 －27］.http://www.isis.ecs.soton.ac.uk/resources/svminfo/.

［22］Ripley B D.Pattern Recognition and Neural Networks［M］.Cambridge:Cambridge University Press，1996.

［23］Blake C L，Merz C J.UCI repository for machine learning databases［EB/OL］.［1998 －10 －15］.http://www.ics.uci.edu/～mlearn/MLRepository.html.