基于泛函变分和变热物性的层冷传热建模
陈水宣,邹 俊,谢 丹
(1.厦门理工学院机械工程系,厦门 361024;2.浙江大学流体传动及控制国家重点实验室,杭州 310027)
在热轧板材生产与控制中,板材的传热温度控制是核心[1]。层流冷却(简称层冷)是板材热轧生产过程的关键环节之一。建立层冷区高精度的传热计算模型,可显著提高温度控制精度,从而改变成品板材的内部晶相组织,提高其加工性能、力学性能和物理性能,获得优质、高韧性、低屈服强度比的钢板[2]。常规的层冷系统采用指数模型计算平均温度,忽略热量在板材厚度方向上的传导,并且将模型中的关键参数(如比热、热导率等物性参数)简化为常数,导致温度预测时误差较大,且由于该类温度模型只是计算板材某断面的平均温度,而现场测温仪所测的是板材表面温度,二者的差异导致温度模型在采用实测和历史数据进行自适应学习时效果不佳[3]。随着用户对产品质量要求的提高以及钢铁企业开发高附加值板材产品的需要,传统的代数温度模型或指数温度模型已经无法满足热轧生产的要求,迫切需要建立适应新产品开发的传热计算模型,以实现板材层冷段温度的精确预测和控制。
1 板材热轧层冷系统
层冷系统安装于精轧出口侧和卷取之间的层流冷却辊道上方。宝钢2050热轧线层冷系统设计有上下两侧,上方主要为了冷却板材上表面,下方冷却板材下表面。轧线侧的顶部水箱系统将更易于控制喷水压力。板材冷却区分为16架,包括主冷区和精冷区,其中主冷区安装136个阀门,精冷区安装24个阀门,共19组水集管。主冷区与精冷区的分界点为精冷区基准点。在精轧出口、层冷冷却中间辊道和卷取机上各布置红外测温仪,其测量点对应于图1中的FDT、MT和CT。

图1 层流冷却系统框图
2 板材层冷温度建模
板材层流冷却是一个时变、非稳态热传导过程。板材内部的温度场不仅随空间位置的变化而变化,而且还随时间的变化而变化[5-6]。板材在冷却过程中的传热包括内部热传导、与运送辊道接触热传导、对流换热、热辐射以及相变放热。研究表明,层冷过程的传热主要是板材的内部热传导、板材表面的对流传热以及板材内部的相变放热,其他传热过程引起的温度变化可以忽略不计。板材在整个层冷过程中交替处于水冷区和空冷区。如图2所示,在空冷区,板材主要是以热辐射的形式传热,而在水冷区则主要以对流换热的形式传热。

图2 板材层冷过程的温度变化
忽略板材在长度方向的热传导,并考虑相变过程产生的热量,建立板材沿厚度、宽度方向温度场控制方程:

式中:T为板材温度(℃);x、y分别为板材厚度、宽度坐标值(m);t为时间(s);λ为热传导率(W/(m·℃));ρ为板材密度(kg/m3);c为时板材的比热为相变过程的潜热变化率。
为求解式(1)的偏微分方程,首先需要确定其初始条件和边界条件。初始条件为板材在精轧出口沿厚度和宽度方向的温度分布,即

边界条件为板材层冷下对环境的热辐射方程(3)和板材与冷却水的对流换热方程(4):

式中:hw1、hw2分别为层流水冷段射流冲击区、稳定膜沸腾区的换热系数(W/(m2·K));Tw1、Tw2分别为射流冲击区、稳定膜沸腾区的冷却水温度(℃);h∞为空冷段热辐射换热系数(W/(m2·K));T∞为环境温度(℃);σ为斯蒂芬-玻尔兹曼常数;ε为黑度。
基于泛函变分原理计算上述热传导偏微分方程,可得到对应的泛函为

值得注意的是,式(5)中的热传导率λ、比热容c和密度ρ是与板材温度变化相关的物性参数,简单地当作常数会给模型计算带来较大的误差。
将板材横断面离散化为E个单元,每单元有m个节点,对于离散化后的每个单元来说则可认为其对应的物性参数为常量,即式(5)的变分式适用于每个单元。离散化后式(5)总泛函I可通过各单元泛函Ie叠加计算,即

取温度插值函数,单元内任意一点的温度T(x,y)与单元节点温度{T}e的关系为 T(x,y)=[N]{T}e,其中[N]=[N1,N2,N3,…,Nm]为基函数矩阵。各单元泛函为

式中:[K]e为单元的刚度矩阵;[C]e为单元的热传导矩阵;{P}e为单元的温度荷载列阵。[K]e、[C]e、[P]e可由下列各式确定:

利用泛函极值的必要条件:

由式(7)和式(11)可得:

使用欧拉方程对温度T进行时间积分:

式中:θ为欧拉参数,取0.5~1;Δt为时间步长。根据前一时间步p的温度Tp,通过式(13)可求得后一时间步p+1的温度值Tp+1。把式(13)代入式(12)得:

求解上式描述的系统方程,即可以获得节点在各离散时间点上的温度,从而计算板材沿厚度和宽度方向上的温度场。
3 变热物性参数实验
热物性参数是表征材料热物理性能的参数,包括密度、比热容和热导率等,是式(1)~(14)的温度场计算所需重要参数。常规传热计算模型中将热物性参数简化为常数,而在层冷过程中板材由于受冷却水冲击,温度变化非常剧烈,特别是对于层冷区发生相变潜热的钢种,其物性参数呈现明显的非线性变化。
取钢种分类表的低、中、高碳钢为本实验钢种,主要化学成分见表1。在宝钢Gleeble热模拟实验机上测量3种钢种样本的热物性参数,测量温度从室温到1 000℃,以每50℃为一个采样点。实验结果表明,密度可近似为常数,但比热和热传导随温度变化剧烈,如图3、4所示。

图3 板材比热随温度变化
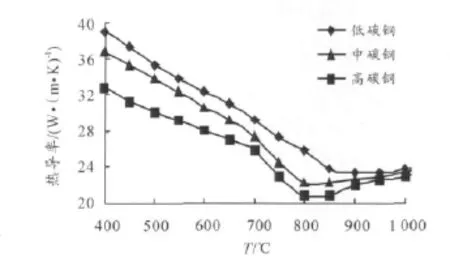
图4 板材热导率随温度变化
由图3可见,在720℃附近比热产生了明显的波动。这是由于板材在层冷过程中产生了相变,相变过程中奥氏体向铁素体、珠光体转变过程的热焓采用多项式回归[9]:

相变过程各相的物性参数为[9]:

式中:cα、cγ、cp分别为奥氏体、铁素体和珠光体的比热(J/(kg·℃));λ为热导率(W/(m·K))。
温度场计算时以钢种为索引号,对比热和热导率的实验数据进行一维温度线性插值,从而获得单元节点温度对应的物性参数值。
4 模型换热系数反算优化
换热系数是反映板材与介质之间热交换能力的重要参数,它与板材规格尺寸、精轧出口温度、冷却水温度和冷却时间等物理参数有关。它们之间存在着复杂的非线性关系。
板材层冷过程主要分为空冷和水冷2个阶段,根据传热方式的不同,首先分别建立带钢上、下表面的空冷和水冷换热系数基本计算模型。
上、下表面的空冷换热系数按式(17)、(18)计算。

其中:σ为斯蒂芬-玻尔兹曼常数;ε为黑度。
上、下表面的水冷换热系数按式(19)计算:

其中:Hc为当前阀门位置,H为起始阀门位置;Vc、h、Te分别为辊道速度、板材厚度、板材表面温度;Vc0、h0、Te0为其对应的基准值;k、α、β、γ 为模型系数。
随着轧制节奏和工艺条件的变更,换热系数需要进一步修正以满足长期应用的稳定性和精度。采用牛顿-拉斐森迭代公式,根据层冷实测的表面温度反算对流换热系数
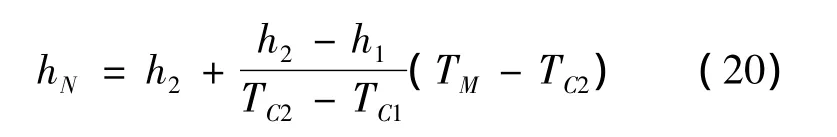
式中:h2、h1为设定的对流换热系数;TC2、TC1为给定h2、h1后的温度计算值;TM为实测温度。
5 现场应用验证
从单卷板材计算和多卷板材连续计算2个方面验证新层冷温度模型,分别如图5、图6所示。
图5为模型计算的单卷板材在整个层冷过程中的温度变化,该板材终轧厚度为6 mm、终轧温度为881.5℃。图中由内到外取板材表面、1/4厚度及中间层3个节点观测其温度计算值。从图5中可以看出,板材表面温度随外界调节变化最为剧烈。板材进入层冷系统的集管水冷区域后,表面温度快速下降,并且在集管间隔开的情况下,表面温度呈现锯齿形变化态势,此时与心部温度相差较大;板材进入空冷区域后,表面温度和中心部温度均缓慢地降低,并且由于表面热流很小、内部热流较大,板材出现快速返温的现象,热量由内部热传导至外部,使得钢板内外温度趋于一致。经模型计算的卷取处温度值为388.9℃,而实测温度为385℃,二者吻合较好。可见,基于泛函变分计算的二维温度模型较真实地反映了板材在层冷过程的温度变化。

图5 板材在层冷过程的温度变化趋势预测
图6为模型进行500条板材的温度预测计算结果。由图6可见,新层冷温度模型计算与实测值吻合良好,模型均方差为10.21℃,相比宝钢2050热轧线原层冷系统14.59℃降低了近30%。由于考虑了物性参数随温度的变化,特别是在相变区中根据实验数值确定了变物性参数的拟合模型,因此新的温度模型特别适用于层冷温度处于相变区的热轧先进高强钢,即热轧双相钢(DP)、相变诱导塑性钢(TRIP)、多相钢(MP)等相变强化高强钢。这对国内钢铁企业实现高附加值热轧高强钢的物理和机械性能控制是十分有意义的。

图6 新模型的温度计算值与实测值对比
6 结论
1)建立以热辐射和冷却水对流换热方程为边界条件的偏微分热传导模型,解决了传统温度解析模型只能计算平均温度的问题,准确地揭示了板材在层冷过程中的温度变化。
2)基于泛函变分原理进行传热方程的离散求解,并且在宝钢Gleeble热模拟实验机上测定3种碳钢样本的密度、比热容和热导率等热物性参数随温度变化的函数关系。该方法特别适用于层冷过程产生相变的低卷取温度高强钢。
3)采用层冷实测温度反算和优化水冷和空冷换热系数。结果表明,该方法提高了温度模型现场应用的稳定性,温度模型计算值与实测值吻合良好。
[1]A Ramirez Lopez,R Aguilar Lopez,M Palomar Pardave.Simulation of heat transfer in steel billets during continuous casting[J].International Journal of Minerals,Metallurgy and Materials,2010,17:403 -416.
[2]Isukapalli B,Sankar K,Mallikarjuna Rao A.Gopala Krishna.Prediction of heat transfer coefficient of steel bars subjected to tempcore process using nonlinear modeling[J].International Journal of Advanced Manufature Technology,2010,47:1159 -1166.
[3]傅新,陈水宣,邹俊,等.热轧带钢精轧过程的混合温度模型[J].浙江大学学报:工学版,2008,42(2):219-223.
[4]孙一康.板材热连轧的模型与控制[M].北京:冶金工业出版社,2002.
[5]金兹伯格 V B.板带轧制工艺学[M].北京:冶金工业出版社,1998.
[6]Heung Nam Han,Jae Kon Lee,Hong Joon Kim,et al.A model for deformation,temperature and phase transformation behavior of steels on run-out table in hot strip mill[J].Journal of Materials Processing Technology ,2002,128:216-225.
[7]Serajzadeh S,Taheri A K,Nejati M,et al.An investigation on strain inhomogeneity in hot strip rolling process[J].Journal of Materials Processing Technology,2002,128:88-99.
[8]Ken-ichiro Mori,Naohiro Oketani.Prediction of coiling conditions of plate in coilbox by controlled FEM simulation[J].International Journal of Machine Tools & Manufacture,1999,39:403 -413.
[9]Siamak Serajzadeh.Prediction of temperature distribution and phase transformation on the run-out table in the process of hot strip rolling[J].Applied Mathematical Modelling,2003,27:861 -875.
[10]Darken L S,Gurry R W.Physical Chemistry of Metals[M].New York:McGraw-Hill,1953.

