用于纵向道路附着系数评估的简化轮胎模型

边明远

(清华大学汽车安全与节能国家重点实验室，北京 100084)

汽车的运动依赖于车轮所受到的路面作用力(力矩)，所有这些路面作用力(力矩)都是车轮滑移(转)率、侧偏角、车轮载荷、道路附着系数以及车身速度等反映地面及车辆动力学状态的参量的函数。地面－车辆力学模型研究的目的在于有效而精确地揭示路面与轮胎界面之间的力学状态和规律，适当地表述上述各参量之间的函数关系。为实时掌握车辆力学状态，探索地面与轮胎间纵向附着系数与车轮滑移率、车速等其他车辆的动力学参数之间的函数关系就显得至关重要。

对于道路附着状况的评估主要有2种方式:一是通过试验仪器测量，二是利用数学模型进行评估。通过仪器测定道路附着系数的试验存在可重复性差、成本高及影响因素多等问题［1］，所以，近年来有关用数学模型计算、评估道路实际附着系数的研究得到了长足的进步。车辆加速度、滑移率、侧偏角等参量与附着系数的变化关系被以数学函数的方式更为精细地描述出来［2－6］。

轮胎模型的构造一般分为物理模型和经验模型2种。物理模型对轮胎本身特性参数的依赖性较大，这些参数往往需要经过试验来获得，这在一定程度上限制了它的应用。鉴于此，采用经验模型对道路附着系数评估的方法得到了广泛应用。

1 经验轮胎模型研究

与理论模型相对应的是经验模型或半经验模型，这些模型通过对大量反映轮胎力特性的试验数据进行分析，能将地面－轮胎之间的力学特性通过含有拟合参数的公式有效地表达出来。Pacejka的魔术公式是在汽车操纵动力学研究领域比较流行的公式，它用三角函数的组合公式拟合试验轮胎数据，用一套形式相同的公式就可以完整地表达纵向力、横向力、回正力矩以及纵向力和横向力联合作用等工况。该模型的一般表达形式为

其中:Y表示侧向力、纵向力或回正力矩;X表示侧偏角α或车轮滑移率S;D、C、B、E分别为确定曲线的峰值、形态、刚度、曲度等因素的参数，由车辆所处的行驶环境、车速、车辆载荷等因素来确定;Sv和Sh分别代表曲线在水平及垂直方向的漂移。

魔术公式基于大量的试验数据拟合而成，对车轮纵向力、侧向力等拟合精度较高。但它是由三角函数组合而成的复杂的非线性函数，而且该模型中需要确定的未知因子也较多，故计算量较大。

近年来，考虑到Pacejka等模型形式复杂、计算量较大等因素，以更简单的方式描述车轮与地面间附着系数的数学模型的研究得到了一定的发展。双线性的轮胎模型、非线性多项式模型、指数－线性多项式组合模型以及双指数多项式模型等在道路纵向附着系数的评估中都有所应用［1，7－9］。总的来说，这些模型在限定的工况下可以实现对道路附着系数的良好估计，但各自也都存在着一定的不足和局限性，魔术公式仍以其对轮胎力学特性的精确描述而成为车辆动力学仿真中参考的一个基准。

2 基于魔术公式的简化轮胎模型

魔术公式应用的一个困难，是其复杂的结构所导致的较大的数学运算量;另外，魔术公式中含有4个待定的未知参数，在车辆动力学仿真过程中首先必须对这些参数进行确定。很多文献中在一定的工况下(如一定路面状况下)往往将这些参数作常数对待，不能实时捕捉道路附着系数随车辆行驶状态以及行驶环境等信息变化的规律。所以，作为一个准静态的计算模型，魔术公式在模拟车轮－地面力学界面的动态特性时有一定的局限性。

很多文献对魔术公式中各因子的确定方法进行了研究。文献［5］通过对试验数据的拟合，将魔术公式中的B、C、D、E等参量描述为车速、车轮载荷、车轮侧偏角、道路状况等因素的函数;文献［10］通过最优化的方式对魔术公式各因子的确定进行了探讨，但忽略了各参量的动态特性，得到的仅是一组静态解;文献［11－12］通过增加2个附加的参数C1和C2来对不同路面状况下魔术公式各因子的变化进行描述。在以上各方法中普遍用到了解多元方程组的手段，但由于魔术公式本身结构的复杂性，使得待解的多元三角函数方程组结构复杂，求解过程运算量大，不利于车辆动力学仿真中对道路附着系数的实时动态模拟。

本文在总结魔术公式的基础上尝试采用更简单的方法对道路纵向附着系数进行评估。考虑道路附着系数随车轮滑移率等因素产生非线性变化的规律，本文采用和魔术公式相似的正弦函数形式，提出一种如式(2)所示的描述车轮纯纵滑工况下纵向道路附着系数的计算模型:

与魔术公式一样，此模型中D、C、B分别为峰值因子、形状因子和刚度因子，它们共同确定μ－S曲线的形状和特征。峰值因子D是在一定工况下纵向附着系数的最大值μxp，相应的车轮滑移率即为最佳车轮滑移率Sxm。通过对试验数据的拟合，路面状况是影响道路附着系数的一个主要因素，不同路面工况的差异都会导致纵向附着特征的不同，而最主要的影响在于道路的峰值附着系数以及相对应的车轮滑移率。表1为几种常见路面状况下纵向的峰值附着系数以及对应的最佳滑移率［5］。

表1 常规路面工况下的纵向附着特征

表1中表达附着特征的参数往往出现在一个范围内，这是因为这些参数除了与路面状况有关之外，还与车速、车轮载荷等因素有关，某一工况下测量的峰值附着系数与最佳滑移率总是与该时刻的车速及载荷等参数相关联。

文献［1］通过综合前人的研究成果以及对试验数据的分析拟合，总结出各种道路工况及行驶条件下路面附着特征参数的公式为

特别规定:当σ=1.2时，

式(2)的模型中虽然各参数的意义与魔术公式中相应的因子意义相同，但由于该模型的形式与魔术公式有所差异，所以各因子的确定方法也不尽相同。根据以上的分析，有

根据式(6)有

在魔术公式中，当用于求解纵向附着系数时，针对干燥的柏油路面，形状因子C被赋予一个固定的常数值1.65。本文通过对各种路况车轮纯纵滑状态下μ－S曲线的基本现状因子值C进行分析，拟合出C值的确定方法为

式中各参量意义同前文所述。

式(3)至式(8)即为任意行驶工况下如式(2)所示的简化轮胎经验模型中各未知参量值的求解方法。该模型将纵向道路附着系数表达为车轮滑移率、车辆行驶速度、车轮载荷、路面状况等因素的非线性函数，有利于对车轮－路面力学界面的动态特性进行实时捕捉。

表2 常见路面的特征因子σ值

3 轮胎模型的拟合结果对比

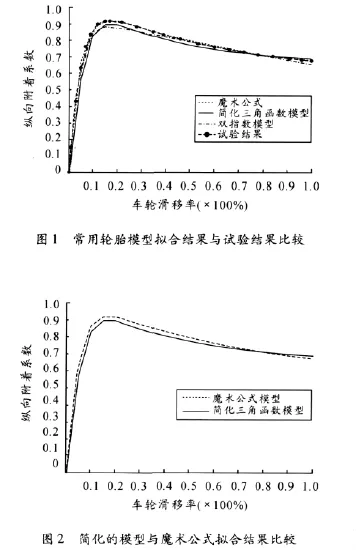
用一辆轻型卡车在干燥的柏油路面上以64 km/h的初速进行制动试验，采用不同的轮胎模型对试验数据进行拟合，并将拟合结果进行对比，结果如图1所示。图2及图3为本文提出的简化轮胎模型与其他模型对干柏油路面工况的拟合结果比较。由对比结果可以看出:Pacejka的魔术公式对纵向附着系数的拟合结果最好，与试验数据吻合良好;双指数组合多项式模型在车轮滑移率值较大时线性化比较明显，在一段区域内与实际附着系数有所偏差。

本文提出的含有3个拟合参数的简化三角函数模型拟合结果与实际试验结果和魔术公式拟合结果比较接近，在车轮滑动的非稳定区域内纵向道路附着系数随车轮滑移率变化的非线性化趋势较双指数组合多项式模型更明显，因而可以更好地表述轮胎与路面的附着变化特征。与魔术公式相比，该模型需要拟合的参数较少，结构较为简单，计算量也较小，能够实时反映轮胎与地面间附着系数的变化，具有较好的实用性。图4显示了用本文提出的简化模型拟合出的不同路面状况下纵向附着系数变化特征。

4 结束语

在车辆实际行驶过程中，车辆的动力学参数处于实时变化的状态，描述地面附着性能的轮胎模型必须要能够捕捉这些变化，并将它们对纵向附着力产生的影响细致地表达出来。本文提出的带有3个参数的简化轮胎模型以更简单的方式将车轮与路面间纵向的附着系数实时表述为路况、车速、载荷以及车轮滑移(滑转)状况的非线性函数，不但能够随时掌握纵向附着系数的变化，而且也能够实时掌握任一路况条件下附着特征参数的变化。该模型引入路况因子概念，并据此对常见路面情况进行划分归类，避免了其他模型中针对一种路况就需要一个拟合公式的弊端，采用一个公式就可以对多种路面附着情况进行模拟，提高了模型的通用性。对试验数据的拟合分析证明该模型是有效的。

［1］边明远.汽车防滑控制系统(ABS/ASR)道路识别技术及车身速度算法研究［D］.北京:北京理工大学，2003.

［2］Chia-shang Liu，Huei Peng.Road Friction Coefficient for Vehicle Path Prediction［J］.Vehicle System Dynamics Supplement，1996，25:413 －425.

［3］Yamazaki S.Study on Real Time Estimation of Tire to Road Friction［J］.Vehicle System Dynamics Supplement，1997(27):225 －233.

［4］Scott Kimbrogh，Krishnaraju Datla.An Effective Means for Implement Wheelslip Control without a Ground Speed Sensor［J］.Vehicle System Dynamics Supplement，1996(25):327－339.

［5］Liu Zhaodu.Mathematical Models of Tire－Longitudinal Road Adhesion and Their Use in the Study of Road Vehicle Dynamics［J］.Journal of Beijing Institute of Technology，1996，5(2):193 －204.

［6］Liu Zhaodu，Ding Nenggen.Influence of Tire Slip Angle on Adhesion Coefficient Characteristic of Road Vehicles［J］.Journal of Beijing Institute of Technology，1997，6(3):292－298.

［7］Luis Alvarez，Jingang Yi.Adaptive emergency braking control in automated highway systems［C］//15 Proceeding of the 38th Conference on Decision＆ Control.Arizona USA:IEEE Press，1999:3740 －3745.

［8］Sun F C，Bian M Y，Chen S Z.Monitoring of longitudinal friction characteristics between the tire and road surface［C］//Proceeding of the 6th International Symposium on Advanced Vehicle Control(AVEC＇02).Hiroshima Japan:JSAE Press，2002.

［9］刘长生.汽车轮胎与公路路面附着系数的研究［J］.公路，2006(5):159－163.

［10］Hu Hai.Methods of Determining the Factors of Pacejka＇s Tyre Model［C］//Proceedings of the Eleventh International Pacific Conference on Automotive Engineering(IPC －11).Shanghai:SAE －China Press，2001.

［11］P Van Der Jagt，Parsons A W.Road surface correction of tire test data［J］.Vehicle System Dynamics，1996(25):147－165.

［12］Tianku Fu.Modeling and performance analysis of ABS systems with nonlinear control［D］.Montreal:Concordia University，2000.