基于破坏形态的重力坝地震易损性研究

钟 红， 李 晓 燕， 林 皋

（大连理工大学 建设工程学部，辽宁 大连 116024）

0 引 言

我国是筑坝大国，遍布全国各地的大坝在国民经济发展过程中扮演着重要的角色.但是大坝的潜在威胁也是巨大的，一旦失事就会直接威胁到下游的生命财产安全.到目前为止，世界上著名的混凝土高坝遭受强震作用产生破坏的实例包括：印度Koyna重力坝在1967年M＝6.5级强震中头部转折处出现严重的水平裂缝，美国Pacoima拱坝在1971年M＝6.6级的San Fernando地震以及1994年M＝6.8级Northridge地震中坝体与重力墩接缝拉开，我国的新丰江大头坝在1962年M＝6.1级地震中大坝头部断裂，伊朗Sefid Rud大头坝在1990年Manjil地震中形成了一条几乎贯穿全坝的头部水平裂缝.

面对大坝严重破坏的震例以及目前随着老坝、病险坝数量的日益增加，重新评价其抗震安全性就显得极其重要.与此相应，大坝的地震风险分析近年来也在抗震安全评价领域得到了广泛的关注与研究.大坝地震风险分析是指对大坝在运行期内遭受地震作用及发生某种程度地震灾害和社会后果概率的研究论证.而作为大坝地震风险研究3个主要组成部分之一的地震易损性分析则可以预测不同地震作用水平下大坝发生各级破损的概率.通过研究大坝地震易损性，一是可以发现拟建坝设计中存在的抗震问题，为优化设计和安全评价提供参考；二是可以发现已建坝的抗震薄弱环节，为科学合理的维修加固决策提供依据.

结构的地震易损性分析最早是从核电站分析开始的，Kennedy等[1、2]给出了两种易损性分析方法（Zion法和SSMRP法）；Hirata等[3]得到了结构反应和地震动参数之间的拟合函数关系，由可靠度概率分布函数给出了相关的易损性概率曲线；C r usu等[4]采用双线性曲线拟合结构反应与地震动参数，提出了一种核电站易损性分析方法.大坝的地震易损性分析方面，Tekie和Ellingwood等[5、6]以Bluestone重力坝为例给出了坝体开裂、坝基滑移以及坝趾的易损性曲线；Papadrakakis等[7]采用连续介质界面单元和蒙特卡罗法进行了静力荷载作用下Scalere大坝的易损性分析；沈怀至等[8]发展了Ellingwood给出的坝体单一破损等级的易损性曲线，提出了坝体－地基系统整体易损性的评价概念.由上可见，以易损性曲线为表达形式的地震易损性分析，作为地震风险评估的一条有效途径，越来越受到国内外学者的关注.但是目前地震区混凝土坝的地震易损性分析发展得还不够完善，至今还没有一个完全确切的科学方法.本文在考虑混凝土材料细观非均匀性以及地震动和材料参数等不确定性因素影响的基础之上，通过对重力坝的地震损伤破坏进行大量的数值模拟提炼出重力坝震害等级划分标准，并以此为基础给出重力坝的地震易损性曲线.

1 混凝土材料的细观非均匀性

大坝混凝土是人工复合材料，从微观层次上以及细观层次上都是极度不均匀的.从细观层次上可将混凝土视为由粗细骨料、水泥砂浆以及两者之间的界面组成的复合材料[9].通常的混凝土坝地震响应分析都将大坝混凝土视为连续均质材料，忽略了混凝土本质上的非均匀性.由于大坝是大体积混凝土材料，将混凝土视为均质材料对获取大坝弹性阶段的响应是合适的，但若需研究其在强震作用下的损伤破坏机理和过程则不尽合理.事实上，若能对混凝土的细观非均匀性作适当的考虑，将可获得对大坝损伤破坏机理的更深入认识.但若严格从细观层次模拟混凝土中各组分，对大坝这种大体积结构来说显然不现实，也无必要.唐春安等[9、10]采用 Weibull分布模型来反映材料细观不均匀性的影响，研究了多种混凝土和岩石试件的断裂过程，得到了与实验相符的结果.借鉴其做法，本文在假定离散后的混凝土有限单元为均质的基础上，认为单元力学参数服从Weibull随机分布，以近似考虑材料细观非均匀性的影响.Weibull分布的概率密度函数如下式所示：

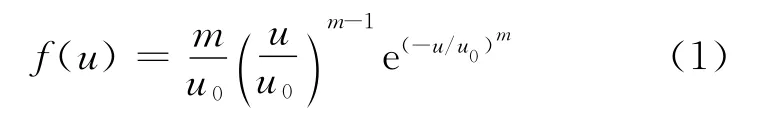
式中：u代表服从该分布的参数（如强度、弹性模量、泊松比等）的取值；u0与参数的平均值相关，但并不等于平均值；均质度m反映了参数取值的离散程度，决定了u0与平均值的相关程度.由图1可知，随着均质度m由小到大变化，单元材料参数概率密度函数由矮而宽变为高而窄，各单元的参数取值趋于均匀化，所有单元参数的平均值越接近于给定的参数u0.换言之，m越大，用以离散结构的混凝土单元材料属性越趋均匀.

图1 Weibull随机分布的概率密度曲线Fig.1 Probability density curve of Weibull random distribution

2 重力坝震害等级划分标准

重力坝在遭受不同地震荷载作用时可能产生不同程度的破损，以此为基础可提炼出重力坝地震破坏的典型模式，并对震害等级进行划分，这是开展大坝地震易损性分析之前所必须完成的工作.严格来讲，震害等级划分应建立在对多座重力坝工程遭受不同地震作用的震害模拟的基础之上，通过统计分析，提炼出典型的震害形态.但本文着眼于提出易损性分析的方法，且重力坝剖面皆为三角形剖面，所以仅以一座典型重力坝为例进行这一工作.这种做法虽难免有失偏颇，但鉴于开展大坝地震风险研究势在必行，希望能有一定的研究价值.

以金安桥碾压混凝土重力坝挡水坝段为研究样本，在考虑混凝土细观非均匀性影响以及地震动不确定性的基础上，通过总计180次非线性有限元分析，提取了重力坝的典型破坏形态，具体计算条件见下文.大坝震后典型形态如图2所示.

图2（a）中大坝基本完好，有微裂缝，但无宏观可见裂缝产生，大坝整体性无劣化.从图2（b）至图2（g），大坝均遭受了不同程度的破损.从计算结果来看，坝头折坡附近、坝踵（坝底）以及下游坝面均是易于开裂的部位，这也是与实际的重力坝震害资料相符的.从图2（b）至图2（d），重力坝的破损程度加剧，但破损一般限于坝体本身，不会造成洪水大量下泻的严重后果.而从图2（e）至图2（g），坝体中下部出现贯穿性的大裂缝，大坝基本丧失挡水功能.

重力坝震害等级的划分，包括划分几个等级及各级之间如何界定，并无严格依据可遵循.本文以上述金安桥重力坝挡水坝段震害模拟的结果为基础，同时考虑两方面因素：（1）考虑不同破损程度导致后果的严重性及修复的难易度；（2）参考房屋建筑震害等级的划分标准[11]，将混凝土坝在地震作用下的震害等级分为基本完好、轻微损伤、中等损伤、严重损伤、溃坝5个级别.各级震害示意于图3.宏观划分标准如下：

图2 典型的大坝破坏形态Fig.2 Typical failure modes of dam

图3 重力坝震害等级划分示意图Fig.3 Seismic damage index of gravity dam

（1）基本完好：坝体基本完好，仅局部有细微裂缝，不影响坝的正常使用.

（2）轻微损伤：坝体局部有较明显裂缝，裂缝长度小于开裂路径长度的1/3，稍加修复即可恢复大坝功能.

（3）中等损伤：坝体多处产生明显裂缝，裂缝长度大于开裂路径的1/3，但未贯通坝体，经修复方能恢复大坝原设计功能.

（4）严重损伤：产生裂缝贯通，坝头断裂，难以修复使用，但不会引发灾害性洪水下泻.

（5）溃坝：坝体中下部断裂，大坝完全破坏，丧失挡水能力，已无修复可能.

3 地震易损性分析步骤

结构的地震易损性分析是研究结构在不同强度地震动激励下产生各级震害的概率，最终的结果以易损性曲线的形式给出.重力坝地震易损性分析方法可有两种：一是根据震后调查的混凝土坝的实际破损状态建立震害等级与地震峰值加速度的统计关系，这种方法可信度较高，但由于受到具体条件的限制，原则上只适用于与数据源类似的情况，而不同的地震环境、场地条件、大坝情况却不相同，因此需要大量的统计资料，实现比较困难，同时考虑到实际重力坝震害资料的匮乏，这种方法难于推广使用；另一种是采用数值模拟手段，对大坝的地震损伤破坏非线性过程进行蒙特卡罗模拟，建立起震害等级与地震峰值加速度的关系，该方法可以弥补实际震害资料的匮乏，不受具体条件的限制，操作简单可行，便于推广应用，但受数值模型的影响较大.

混凝土重力坝的地震易损性分析除了考虑输入地震动幅值的随机性以外，还考虑了大坝混凝土材料参数的不确定性，包括混凝土弹性模量、抗拉强度、泊松比、密度、阻尼比等.具体而言，对材料参数根据其概率分布特征，利用随机抽样方法获得多组样本，并对每组样本采用 Weibull模型来近似考虑混凝土细观不均匀性的影响，进而针对不同地震水平作用模拟大坝地震损伤破坏过程[12].通过将大坝最终的形态与大坝震害等级划分标准相对照，即可确定不同地震动幅值输入时坝体产生各级破损的概率分布，进而得到大坝的地震易损性曲线.基本流程如图4所示.

图4 重力坝地震易损性分析流程图Fig.4 Flow chart for seismic fragility analysis of a gravity dam

4 金安桥混凝土重力坝的易损性分析

4.1 基本数据及模型参数

以建设中的金安桥碾压混凝土重力坝挡水坝段为例，研究了混凝土重力坝的地震易损性.金安桥水电站位于金沙江中游河段，坝顶长640m，最大坝高160.0m，正常蓄水位1 418.0m，淤沙高程1 335.0m，下游水位1 312.0m，挡水坝段高114m.坝体承受的静力作用包括：坝体自重、扬压力和对应于正常蓄水位的水压力.动力计算中，动水压力采用Westergaard附加质量模型模拟.地震动同时在水平向和竖直向输入，竖向加速度幅值为水平向的2/3.地震加速度时程以归一化的形式示于图5.

对地基的模拟采用无质量地基假定，模拟范围为坝底以下及坝上游、下游方向各2倍坝高.重力坝－地基系统全部采用四边形等参元进行网格剖分，坝体部分单元尺寸为0.3m，地基部分单元尺寸最大为10m.整个重力坝－地基系统共剖分64 690个单元，65 244个节点.其中坝体部分为59 665个单元，60 260个节点.图6为重力坝－地基系统有限元模型及弹性模量分布.图中的灰度代表了单元弹性模量的相对大小，颜色越浅的单元弹性模量越高.

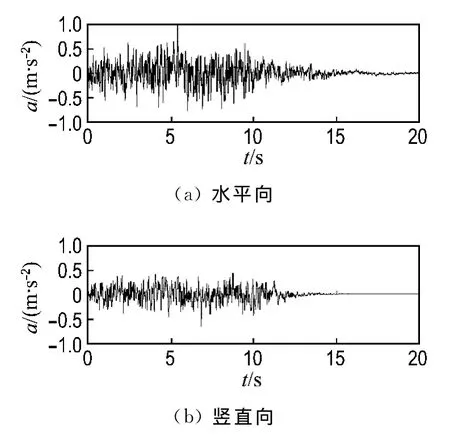
图5 地震加速度时程归一化曲线Fig.5 Unit－acceleration time history curve ofthe earthquake input

图6 大坝－地基有限元离散及弹性模量分布Fig.6 Finite element discretization of dam－foundation system and distribution of elastic modulus

考虑了大坝混凝土的分区，图6中1、2、3区的混凝土标号分别为C15、C20、C25，对应材料参数：静态抗压强度fc分别为15、20、25MPa，弹性模量分别为22.0、25.5、28.0GPa，泊松比0.17，密度2 400kg/m3.分析采用的不确定性参数的概率分布假定为弹性模量、抗拉强度、泊松比、密度等不确定性因素的统计特征均按正态分布表示；阻尼比在一个较大空间（0.03，0.15）内满足均匀分布[13].兼顾计算量和随机分布样本数的要求，对各参数均生成了30组样本.动强度和动弹性模量在对应静参数基础上均提高30%.地基的等效动弹性模量为16.5GPa，泊松比为0.25，密度为2 400kg/m3，阻尼比为5%.大坝的设计地震波加速度峰值为0.399g，考虑到地震动的不确定性，另分析了加速度幅值为0.2g、0.3g、0.5g、0.6g、0.8g的情况.研究了金安桥重力坝在静动组合荷载作用下的地震易损性.

4.2 易损性分析结果

将30组重力坝－地基系统材料参数的随机样本与前述对应6个加速度幅值的地震动输入分别组合，共进行了180个样本的非线性有限元计算，得到了180组大坝的响应.大坝有完好的情况，有出现裂缝但未贯穿的情况，也有裂缝贯穿导致溃坝的情况.提炼出几种具有代表性的大坝破坏形态如图2所示.根据大坝的震害等级划分标准，对180个计算样本的非线性时程模拟破损程度进行了统计分析，得到了以地震峰值加速度为变量的易损性曲线，如图7所示（P为不同震害状态超越概率）.

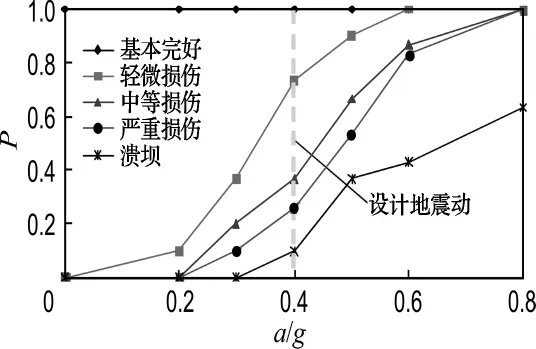
图7 坝体易损性曲线Fig.7 Fragility curves of dam

由图7可以看出，随着地震峰值加速度的增大，坝体处于基本完好状态的概率越来越小，而溃坝的概率则是越来越大.由于考虑了混凝土材料的不确定性以及细观非均匀性，低地震动水平下大坝严重损伤和高地震动水平下大坝轻微损伤甚至基本完好的情况也是存在的，但大坝的破坏概率总体上随着地震动水平的增大而增大，这与实际情况是一致的.另外，图7的易损性曲线表明：大坝在各级地震动作用下都有产生震害的可能，地震动幅值增大，震害程度加剧；设计地震动作用时，产生中等及以上损伤的概率是36.67%，溃坝概率为10.00%；2倍设计地震动作用时，溃坝概率达到63.33%.

根据以上坝体的易损性分析以及破坏模式的统计研究可知，金安桥混凝土重力坝在设计基准期100a超越概率2%的地震动作用（设计地震峰值加速度0.399g）条件下，需要在坝头、上游折坡处、坝踵、上下游坝面采取加固措施.

5 结 语

在考虑大坝混凝土的细观非均匀性影响以及混凝土材料不确定性、地震动输入不确定性的基础上，通过重力坝地震损伤破坏过程的大量数值模拟研究了重力坝的地震破坏形态，据此提出了包括基本完好、轻微损伤、中等损伤、严重损伤及溃坝5个等级在内的重力坝震害等级划分标准以及以此为基础的重力坝地震易损性分析方法.

在设计地震动作用下，金安桥混凝土重力坝在无其他抗震措施条件下出现中等及以上损伤的地震易损性概率为36.67%，出现溃坝的概率为10.00%.从以上数据来看，金安桥重力坝需要进行抗震加固来满足设计地震动下的性能要求.本文提出的易损性分析方法以及给出的易损性曲线对优化大坝的抗震设计以及维修加固决策都具有一定的应用价值，同时也为地震风险评估提供了参考.

[1] KENNEDY R P.Seismic fragilities for nuclear power plant risk studies [J].Nuclear Engineering and Design，1980，59（2）：315－338

[2] KENNEDY R P， RAVINDRA M K.Seismic fragilities for nuclear power plant risk studies [J].Nuclear Engineering and Design，1984，79（1）：47－68

[3] HIRATA K，KOBAYASHI Y，KAMEDA H，etal.Fragility of seismically isolated FBR structure [J].Nuclear Engineering and Design，1991，128（2）：227－236

[4] C R USU A，VULPE A.Fragility estimation for seismically isolated nuclear structures by high confidence low probability of failure values and bilinear regression [J]. Nuclear Engineering and Design，1996，160（3）：287－297

[5] TEKIE P B，ELLINGWOOD B R.Seismic fragility assessment of concrete gravity dams[J].Earthquake Engineering and Structural Dynamics，2003，32（14）：2221－2240

[6] ELLINGWOOD B R，TEKIE P B.Fragility analysis of concrete gravity dams [J]. Journal of Infrastructure Systems，2001，7（2）：41－48

[7] PAPADRAKAKIS M， PAPADOPOULOS V.Vulnerability analysis of large concrete dams using the continuum strong discontinuity approach and neural networks[J].Structural Safety，2008，30（3）：217－235

[8] 沈怀至，金 峰，张楚汉.基于性能的重力坝－地基系统地震易损性分析[J].工程力学，2008，25（12）：86－91

[9] 唐春安，朱万成.混凝土损伤与断裂——数值试验[M].北京：科学出版社，2003

[10] 唐春安，王述红，傅宇方.岩石破裂过程数值试验[M].北京：科学出版社，2003

[11] 尹之潜.地震灾害损失预测研究[J].地震工程与工程振动，1991，11（4）：87－96

[12] ZHONG H，LIN G，LI X，etal.Seismic failure modeling of concrete dams considering heterogeneity of concrete [J].Soil Dynamics and Earthquake Engineering，2011，31：1678－1689

[13] ASCE.Seismic analysis and design：Chapter 5[M]//Structural Analysis and Design of Nuclear Plant Facilities.Reston：ASCE，1980