微细电火花加工微孔时加工作用力影响
李 剑 忠, 张 余 升, 栾 纪 杰, 余 祖 元
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.上海航天设备制造总厂,上海 200245;3.无锡微研有限公司,江苏 无锡 214072)
0 引 言
电火花加工中,虽然工具电极和工件之间没有直接的机械接触,但却存在有多种力的作用,这些力统称为加工作用力.其主要来源于加工过程中气泡的膨胀力和破裂冲击力[1]、两个电极之间的静电力和电磁力[1、2]、工作液流动产生的冲刷力[3]以及放电瞬间产生的爆炸力[4]等.对此已有多位专家学者进行了研究.例如Kimoto测量出油中放电时两极之间产生的加工作用力,并发现该力主要是由于两极间的大量气泡不断膨胀和压缩产生的[5];Kunieda等利用压电陶瓷力敏传感器得到了加工作用力的变化曲线,但测量结果中含有一22kHz的干扰[6];Tohi等应用分离式霍普金森杆方法测得了液体中单次脉冲放电时两极间加工作用力的变化曲线,结果发现该力峰值在50N以上[7];Puri等研究发现,线切割中加工作用力的存在导致线电极产生振动,振幅大于16 μm[8].但这些研究主要都是针对常规电火花加工或线切割进行的,都是在电极尺寸较大的情况下得出的结论,而对微细电火花加工微孔过程中加工作用力的影响则至今未见报道.
微细电火花加工微孔过程中,由于工具电极的直径仅为微米量级,长度是毫米量级,加工作用力的影响将尤其显著.本文通过卧式微细电火花加工设备实际研究这一影响,并针对工具电极受力的几种情况,根据弹性力学经典理论求解加工过程中力学影响的数学模型,最后结合实验结果对理论模型进行分析验证.
1 加工作用力对微孔加工的影响
加工作用力对微细电火花加工微细孔的影响通过在自制的卧式微细电火花加工装置上实验进行研究.图1为实验装置的照片.

图1 实验装置Fig.1 Experimental equipment
为了研究不同的电极材料、电极转速以及工作液等的影响,实验共分为16组进行.实验中采用的加工电压均为80V,放电电容均为1 000 pF,工件材料均为304不锈钢.表1所列为各组实验中所采用的其他加工条件.
每组实验的步骤均为先通过 WEDG[9]单元制备微细电极,再驱动X-Y-Z工作台移动电极探测工件表面,确定加工的起点位置,然后开始实验加工微孔.加工中当电极进给达0.2mm时将电极退出加工区并将电极从初始长度截去0.4mm以避免电极端部变形影响后续孔的加工,然后再加工下一个微孔.如此重复直至电极剩余长度不足以再次加工下一个微孔时结束本组实验.结束后清洗工件和电极,并测量电极剩余长度和所有加工孔的直径.
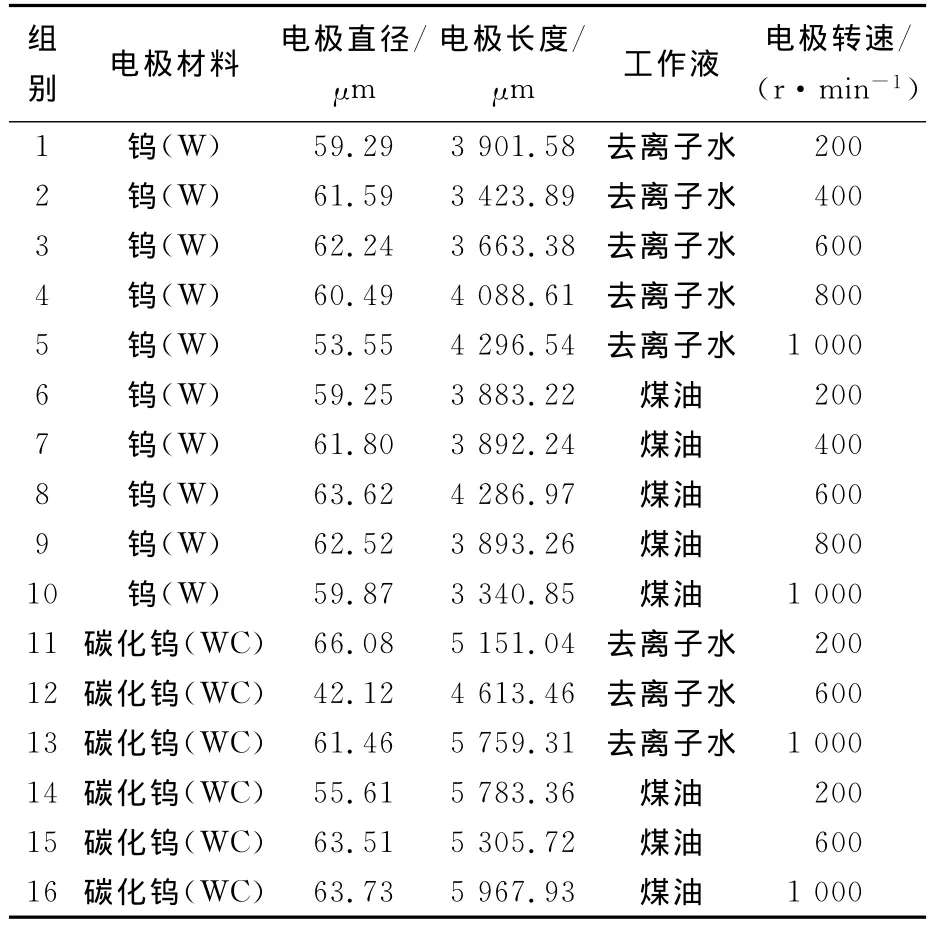
表1 实验加工条件Tab.1 Experimental processing conditions
分析16组实验的结果发现,每组实验加工出的孔径都由大到小顺次排列,最先加工出的孔径最大,最后加工出的孔径最小,而加工条件的改变对这一规律并没有显著的影响.这与每组实验中电极长度的逐步截短是十分吻合的,从而间接证明了加工作用力的存在与影响.孔径的顺次减小是由于加工过程中电极在加工作用力影响下弯曲变形所致,电极越短则弯曲变形越小,加工的孔径也越小.表2是所有16组实验的部分测量结果.图2是其中第7组和第14组实验中加工后所有微孔的显微照片.

表2 部分实验结果Tab.2 Partial experimental results

图2 实验结果的显微照片Fig.2 Micrographs of experimental results
2 加工作用力影响的理论模型
在微细电火花卧式加工装置中,电极为悬臂梁,同时考虑到下列因素:
(1)电极直径不变时,电极自身所受的重力为均布荷载,如图3中q所示;
(2)加工条件相同时,同一电极所受的加工作用力(不包含重力)均值与电极长度无关;
(3)加工孔的外表面时,电极承受的加工作用力仅作用在电极末端,如图3中Fn和Ft所示;
(4)电极不可伸长,且电极受力后的弯曲变形为弹性小变形;
(5)电极直径远小于电极夹持部分的直径,故其弯曲变形仅发生在图4中L所示的直线部分.
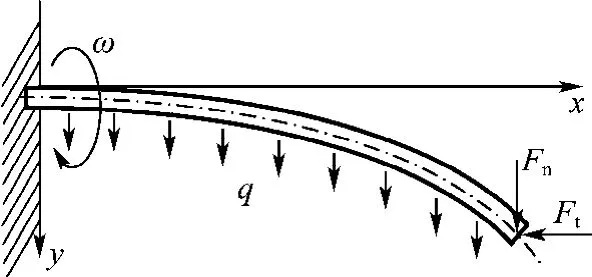
图3 悬臂梁模型Fig.3 Model of cantilever
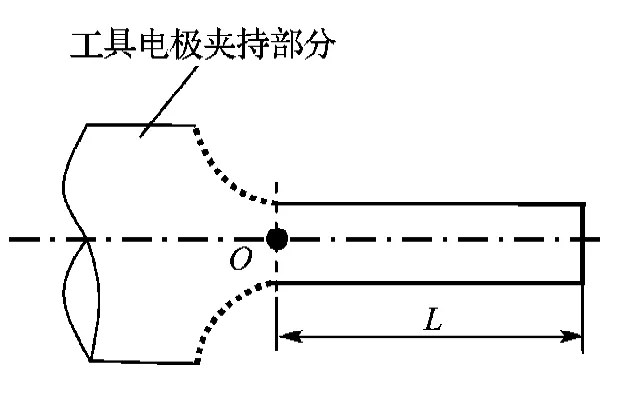
图4 电极形状Fig.4 Electrode shape
为此,根据弹性力学中经典Bernoulli-Euler杆件理论[10],当用ω、d、ρ和E分别表示电极的转速、电极直径、电极材料密度与弹性模量时,计算获得电极在3种不同的加工作用力影响下的弯曲变形,即加工作用力影响模型如下:
(1)电极受径向力作用不考虑其旋转和质量时的影响模型(模型Ⅰ)
忽略电极自身的质量、轴向力和旋转的影响(即令图3中的ω=0,Ft=0,q=0),只考虑电极受恒定的径向力Fn作用时产生的变形为

式中:I为电极的主惯性矩,I=πd4/64,从而得电极仅受径向力Fn作用时的末端最大变形量为

(2)电极受径向力作用考虑其旋转和质量时的影响模型(模型Ⅱ)
忽略轴向力(即令图3中的Ft=0)并考虑电极质量和旋转影响时,电极在径向力Fn作用下产生的变形应满足如下的微分方程[10]:

该方程解的一般形式为
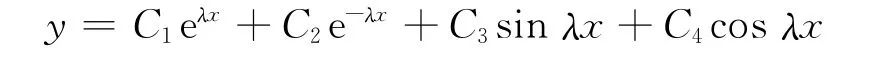
式中:λ= (ω2ρ0/EI)1/4;ρ0=πd2ρ/4,为电极单位长度的质量;I=πd4/64,为电极的主惯性矩.
考虑到方程应满足的边界条件:

解得方程中的常数C1、C2、C3、C4的值分别为
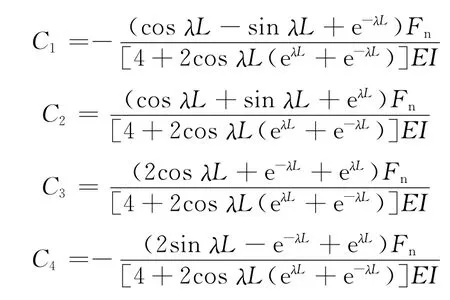
(3)电极受轴向力作用考虑其旋转和质量时的影响模型(模型Ⅲ)
忽略径向力(即图3中的Fn=0)并考虑电极质量和旋转影响时,根据弹性力学中经典Bernoulli-Euler杆件理论,可得电极在轴向力Ft作用下产生的末端变形为[10]

上式中各参数分别为

3 理论模型的验证与分析
根据上述3种理论模型,将前述16组实验中每组结果的首孔与末孔的半径差作为电极的末端变形,采用迭代逼近的方法分别反求出相应的Fn或Ft,然后再根据所获得的48组数据中的Fn和Ft,以及每一组实验中加工其他各孔前的对应电极长度,由理论模型求出每一组实验中加工其他各孔时的电极的弯曲变形量,并与实际加工后该孔与末孔的半径差的测量结果对比,从而验证理论模型的使用效果.计算中取钨的弹性模量为36.5GPa,其密度为1.935×104kg/m3,取碳化钨的弹性模量为585GPa,其密度为1.375×104kg/m3.
下面仅以较好的第7组和较差的第14组实验数据说明对理论模型的验证情况.表3列出了根据第7组和第14组实验结果中首孔与末孔的半径差反求获得的Fn和Ft,图5表明了根据这两组实验中各加工孔的测量结果对理论模型的验证情况,表4则给出了所有16组实验中模型计算结果与实际测量值之间的平均误差与均方差的统计结果.

表3 理论模型反求结果Tab.3 Reverse calculation results of theoretical models

图5 理论计算值与实验值对比Fig.5 Comparison of the theoretical values and the experimental values

表4 不同模型的统计结果Tab.4 Statistical results of the models
从图5和表4可以看出,模型Ⅱ的理论计算结果与实际测量值吻合最好,能够较好地解释微细电火花加工微孔过程中,当加工条件不变时,工具电极越长加工孔径越大的孔径随电极长度同向变化的现象,从理论上揭示了加工作用力对微孔加工过程的影响.在加工过程中,随着电极长度的增加,电极在加工作用力作用下的弯曲变形将随之增大,从而导致同样直径的电极在长度不同时加工出的孔径不等,电极越长,孔径越大.模型Ⅰ虽然没有考虑电极质量及其旋转影响,但计算结果与模型Ⅱ近于重合(见图5中模型Ⅰ和模型Ⅱ曲线),只是误差稍大,说明当电极微小时,其质量和旋转的影响近乎可以忽略.模型Ⅲ由于计算误差最大(见表4),说明其偏离实际情况较远,加工过程中电极弯曲变形受径向力Fn作用远较轴向力Ft敏感、显著.
理论计算与实验结果之间存在误差的主要原因在于:难以求解电极在工作状态下真实受力的影响模型,即难以综合考虑径向力和轴向力对电极变形的联合影响,同时加工作用力的数值逼近反求计算以及加工孔径的测量也都存在有一定误差.但由图5和表4可以看出,由于模型计算结果总是小于实测值,在计算模型中加入适当的修正系数,将能进一步减小计算误差,提高模型的准确程度.
4 结 论
(1)在微细电火花加工微孔过程中,虽然工具电极和工件之间没有直接的机械接触,但加工作用力的影响不容忽视.当加工条件和电极直径相同时,加工孔径与工具电极的长度呈同方向变化,电极越长则加工出的孔径越大,且加工条件改变时,这一规律没有显著变化.因此,微细电火花加工微孔时必须考虑电极长度的影响.
(2)基于弹性力学理论获得的微孔加工过程中加工作用力的影响模型,特别是径向力影响模型,能够较好地解释上述现象,计算结果几乎不受微小电极的质量及其旋转因素的影响,且与实际测量值非常接近,从理论上揭示了加工作用力对微孔加工过程的影响.电火花加工微孔过程中,由于加工作用力特别是微小径向力的存在,使电极的弯曲变形随电极长度增加而增大,从而导致同样直径的电极在长度不同时加工出的孔径大小不等.
致谢:大连理工大学工业装备结构分析国家重点实验室的吴承伟教授在理论模型求解过程中给予了帮助.
[1] KUNIEDA M,TOHI M,OHSAKO Y.Reaction forces observed in pulse discharges of EDM [J].International Journal of Electrical Machining,2003,8:51-56
[2] HERRERO A,AZCARATE S,REES A,etal.Influence of force components on thin wire EDM [C]//International Conference on Multi-Material Micro-Manufacture (4M).Cardiff:Whittles Publishers,2008
[3] KATZ Z,TIBBLES C J.Analysis of micro-scale EDM process[J].International Journal of Advanced Manufacturing Technology,2005,25:923-928
[4] 胡玉景,张建华,任生峰,等.不同电规准条件下硬质合金电火花加工性能的研究 [J].工具技术,2006(1):26-28
[5] 木本保夫.放電加工における衝撃力について[J].電氣學會雜誌,1961,81(871):1877-1885
[6] KUNIEDA M,ADACHI Y,YOSHIDA M.Study on process reaction force generated by discharge in EDM [C]//Proceeding of the 2nd International Conference on Machining and Measurement of Sculptured Surfaces. Krakow:Institute of Metal Cutting,2000
[7] 土肥麻里子,小松利直,国枝正典.ホプキンソン棒法を用いた放電加工反力の測定[J].精密工学会誌,2002,68(6):822-826
[8] PURI A B,BHATTACHARYYA B.Modelling and analysis of the wire-tool vibration in wire-cut EDM[J].Journal of Materials Processing Technology,2003,141:295-301
[9] MASUZAWA T,FIJINO M,KOBAYASHI K.Wire electro discharge grinding for micromachining[J].CIRP Annals,1985,34(1):431-434
[10] TEODOR M A.Stability Theory of Elastic Rods[M].Singapore:World Scientific Press,1997

