新陈代谢灰色模型对广东省肺结核报告发病率的预测分析

蒋莉 钟球 周琳 李建伟 连永娥

新陈代谢灰色模型对广东省肺结核报告发病率的预测分析

蒋莉 钟球 周琳 李建伟 连永娥

目的利用新陈代谢灰色模型预测广东省结核病发病趋势，为制定结核病的防控措施提供依据>。方法根据广东省2001—2011年肺结核报告发病率数据分别建立常规灰色模型［grey model（1，1），简称GM（1，1）］和新陈代谢灰色模型［简称新陈代谢GM（1，1）模型］。通过短序列与长序列预测结果，比较两种预测精度和准确性，选择最优的模型进行外推预测。模型的预测精度以后验差比值C和小误差概率P表示，精度等级越小越好，精度一级最好，四级不合格>。结果不同维度的新陈代谢GM（1，1）模型的误差小于相应维度的常规GM（1，1）模型，短序列预测的误差小于长序列。5维新陈代谢GM（1，1）模型精度检验指标均为一级，后验差比值C和小误差概率P分别为0.14和1>。结论新陈代谢GM（1，1）模型是处理此类数据较为理想的模型，5维新陈代谢GM（1，1）模型对于广东省肺结核报告发病率的预测具有一定优势。

结核，肺／流行病学； 发病率； 预测； 模型，统计学； 结核，肺／预防和控制； 广东省

结核病被列为我国重大传染病之一，是严重危害人民群众健康的呼吸道传染病。根据WHO的统计，我国是全球22个结核病流行严重的国家之一，同时也是全球27个耐多药结核病流行严重的国家之一。目前我国结核病年发病人数约为130万，占全球发病的14.3%，位居全球第2位［1－2］。2010年广东省第五次结核病流行病学抽样调查结果推算，全省现有活动性肺结核患者17.1万，其中涂阳肺结核患者3万［3］。因此，及时掌握当前结核病流行趋势，推断其未来变化，对于制定针对性的防治策略十分重要。

结核病的估计预测是掌握结核病流行现状及趋势、政策开发、项目设计和评价，以及资源配置的基础。因此，笔者根据广东省2001—2011年的肺结核报告发病资料，利用灰色系统预测模型，探求肺结核流行规律，对广东省肺结核的报告发病情况进行中长期的预测，以可信的数据资料为提出有针对性的防治措施提供实证性的依据。

材料和方法

一、资料来源

二、研究方法

采用 MATLAB2007R软件编写程序，利用2001年至2010年肺结核报告发病率分别建立常规灰色模型［grey model（1，1），简称 GM（1，1）］和新陈代谢灰色模型［简称新陈代谢GM（1，1）模型］，用2011年的数据评价模型的预测效果，对2012—2015年广东省肺结核报告发病率进行预测和分析。

三、灰色模型的建立［4］

（一）常规 GM（1，1）模型

设原始灰色数列资料为：χ0（1），χ0（2），…，χ0（n），记为χ（0）＝（χ0（1），χ0（2），…，χ0（n）），对之进行一次累加，累加数列克服了原始数列的波动性和随机性，转化为规律性较强的递增数列。

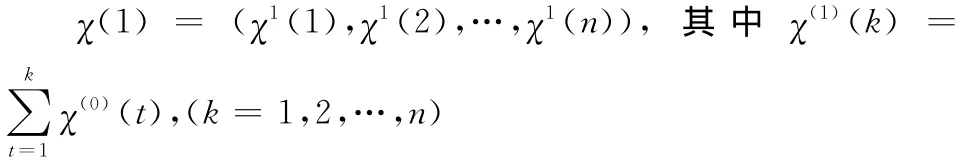
GM（1，1）模型是有一阶微分方程构成的动态模型：

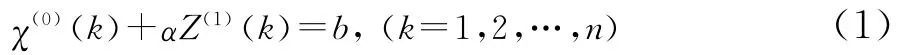
其中Z（1）（k）是χ（1）（k）的紧邻均值生成序列，即：Z（1）（k＋1）＝0.5［χ（1）（k＋1）＋χ（1）（k）］，式（1）的白化方程为：

其中α为发展系数，b为灰色作用量，由最小二乘法可得：

求得方程的解，即时间响应函数为：

大学教学要想达成提高学生基本素质，培养创新人才，实现大学生优质发展的目标，首先要求高校教师转变教学观与课程观，尊重学生主体地位，注重教师和学生之间的交流与合作。把握教师教学观与课程观转变的趋向及其与高校课堂教学发展的关系。这对于大学教学改革的推进有着积极的意义。

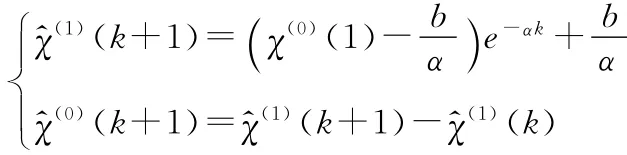
（二）新陈代谢 GM（1，1）模型

采用常规GM（1，1）模型预测，精度较高的仅仅是最近几个数据，离现实时刻越远，其预测意义越弱。为反映未来的随机扰动或者驱动因素对灰色系统的影响，提高预测精确度，可采用新陈代谢GM（1，1）模型［4］。即：在原始数据序列χ（0）＝（χ0（1），χ0（2），…，χ0（n））中，置入最新信息χ（0）（n＋1），去掉最老信息χ（0）（1），用χ（0）＝（χ0（1），χ0（2），…，χ0（n），χ（0）（n＋1））建立的模型即为新陈代谢 GM（1，1）模型。此外，在实际建模中，选择不同维数的序列建模，能够得到不同的预测值，因此笔者建立不同维数的新陈代谢GM（1，1）模型，从中选取合适维数的新陈代谢GM（1，1）模型进行预测。

（三）模型精度的检验

GM（1，1）模型的拟合精度，通常由平均相对误差、后验差比值和小误差频率等指标的大小来判定。

后验差比值：C＝S2／S1其中：

模型精度分类见表1，模型精度级别＝max｛C所属等级；P所属等级｝。

表1 GM（1，1）模型预测精度等级判断

四、软件选用

上述建模均在MATLAB2007R软件上通过编程方式实现。

结 果

一、广东省结核病各年报告发病率情况

广东省2001—2011年各年肺结核患者报告发病率见表2。

二、预测模型的建立

为筛选适当预测模型，考虑到灰色模型建模数据不少于4维的要求，笔者分别选4～10维肺结核患者报告发病率序列，建立常规GM（1，1）模型和新陈代谢GM（1，1）模型，对2009和2010年广东省肺结核报告发病率进行检验性预测，其结果见表3、4。

表2 广东省2001—2011年各年肺结核患者报告发病率情况

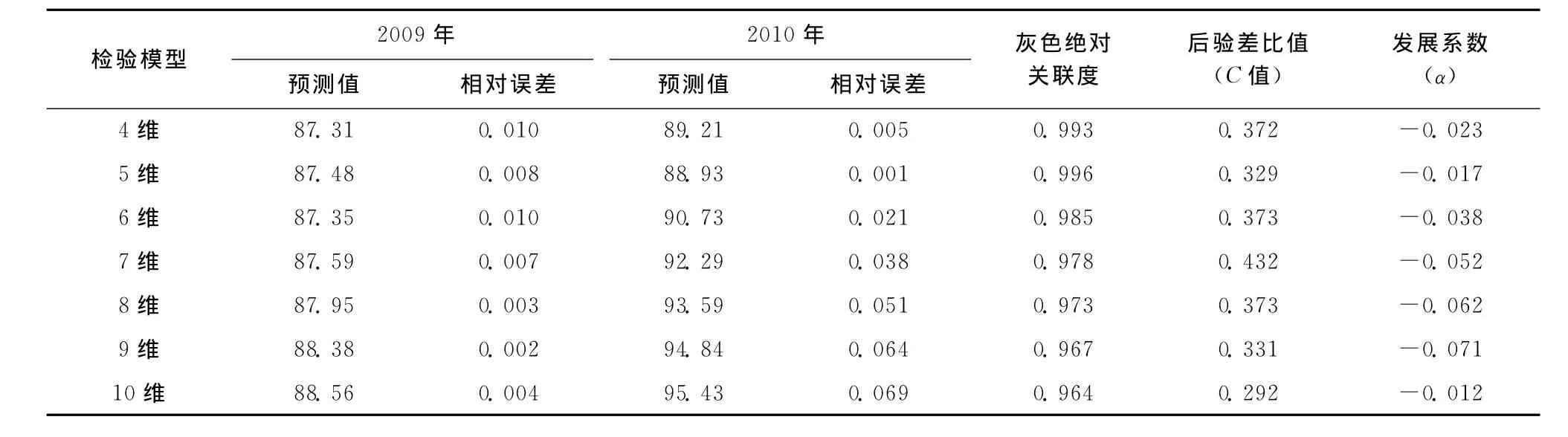
表3 常规灰色GM（1，1）模型对肺结核患者报告发病率的检验性预测

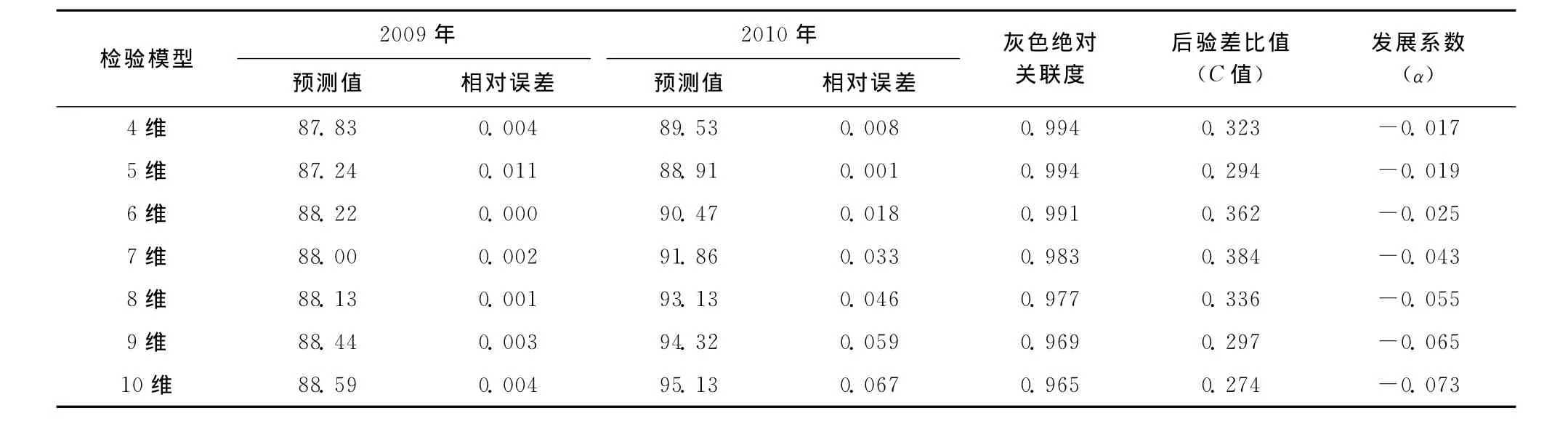
表4 新陈代谢GM（1，1）模型对肺结核患者报告发病率的检验性预测

由表3、4可知，短序列预测的误差通常小于长序列，而新陈代谢GM（1，1）的误差又小于对应的常规GM（1，1），预测的时间越远，误差越大。

表5 新陈代谢GM（1，1）模型对2011年肺结核报告发病率的预测

由表5可见，5维新陈代谢GM（1，1）模型的误差最小，其绝对误差和相对误差分别为2.81和0.032。结合表3、4分析，5维常规灰色 GM（1，1）模型和5维新陈代谢GM（1，1）模型后验差比值分别为0.329和0.294，小于0.35；发展系数α分别为－0.017和－0.019。

三、广东省结核病报告发病率预测

通过上述分析，根据广东省肺结核报告发病率原始数据序列，先建立常规5维灰色GM（1，1）模型，计算后验差比值C为0.14，小概率误差P为1，预测精度为一级，可以进行中长期预测。根据常规5维灰色GM（1，1）模型建立的5维新陈代谢GM（1，1）模型，对广东省结核病报告发病率变化趋势进行分析。2012年至2015年广东省肺结核报告发病率预测值分别为92.36／10万，94.13／10万，95.93／10万和97.77／10万。

讨 论

由于结核病监测受到多种因素和干预措施的影响，导致当前结核病疫情监测指标的敏感度和特异度不强，监测信息不能充分反映结核病的实际发病和死亡情况，从而难以及时预测结核病的发病、流行和暴发，不能及时采取有效的应对措施，导致结核病发病和死亡人数的增加［5］。

目前对结核病报告发病率的预测方法较多，如：20世纪60～70年代的联列递推微分方程组，20世纪90年代的回归模型（直线或曲线模型、指数模型、多项式模型）、指数平滑法及时间序列（ARIMA）模型等方法层出不穷。但这些方法对样本的数量及样本的分布规律有一定的要求，计算方法也较为复杂，有时甚至还可能出现定量结果与定性结果不符等现象，因此在应用上受到一定的限制。而灰色系统模型对样本量及分布没有非常严格的要求，具有较强的适用性。新陈代谢灰色模型除了具有常规灰色模型计算简单，所需数据少，无需先验信息等特点外，还因为它不断更新建模数据，去除陈旧数据，使得预测精度得以提高，预测值比常规灰色模型更接近实际值［6－8］。

笔者利用常规GM（1，1）模型建立的5维新陈代谢GM（1，1）模型，得到预测模型均方差比值为0.294，发展系数为－0.019，对2011年肺结核报告发病率进行检验性预测，绝对误差为2.81，相对误差为0.032，取得的预测结果与实际结果基本一致，预测误差在10%以内。从预测角度看，该模型用于结核病报告发病率的预测是可行的，合理的和可接受的，预测效果较为理想。假定目前格局不变的情况下，对广东省2012—2015年肺结核报告发病率进行预测，未来广东省结核病疫情不会发生较大的变化。提示，广东省以现代结核病控制策略为核心开展的结核病防治工作卓有成效，特别是近年来“政府领导、多部门合作、全社会参与”的结核病防治工作机制，对全省结核病控制工作的可持续发展起到了积极的作用。该模型的预测结果可以与日常监测相结合，及时发现异常情况。同时可以对新的政策措施实施效果进行评价，为广东省结核病预警提供技术参数，对全省结核病报告发病率的估计和预测起一定的借鉴作用。

此外，为使预测精度更为准确，充分发挥新陈代谢GM（1，1）模型优越性，可考虑进行多次预测，每次预测的时间段尽量少一些。如在精确度检验时，发现误差较大，可考虑定义适当序列算子，如二阶弱化算子，对算子作用后的序列建立模型［9］，以达到提高模型预测精确度的最终目的。研究模型不是一劳永逸的，不能作为永久的预测工具，实际工作中应该不断积累，不断更新模型，才能获得较为准确的预测效果。

［1］World Health Organization.Global tuberculosis control：surveillance，planning，financing.Geneva：WHO，2006.

［2］Borgdorff MW.New measurable indicator for tuberculosis case detection.Emerg Infect Dis，2004，10（9）：1523-1528.

［3］钟球，尹建军，钱明，等.广东省第五次结核病流行病学抽样调查分析.中国防痨杂志，2011，33（6）：317-322.

［4］刘思峰，党耀国，方志耕.灰色系统理论及其应用.3版.北京：科学出版社，2004：141-142.

［5］钟球，蒋莉，周琳，等.广东省结核病发病趋势的时间序列分析.中国防痨杂志，2010，32（9）：515-518.

［6］白先春，李炳俊.基于新陈代谢GM（1，1）模型的我国人口城市化水平分析.统计决策，2006，（5）：40-41.

［7］Azuma Y.A simple simulation model of tuberculosis epidemiology for use without large-scale computers.Bull World Health Organ，1975，52（3）：313-322.

［8］Pilheu JA.Tuberculosis 2000：problems and solutions.Int J Tuberc Lung Dis，1998，2（9）：696-703.

［9］何穗智，欧顺云，邓卓燊，等.香港 HIV／AIDS新陈代谢GM（1，1）模型与预测分析.数理医药学杂志，2007，20（6）：751-753.

Application of the grey model of metabolism for prediction of the pulmonary tuberculosis incidence in Guangdong pro-vince

JIANG Li，ZHONG Qiu，ZHOU Lin，LI Jian-wei，LIAN Yong-e.Center for Tuberculosis Control of GuangdongProvince，Guangzhou 510630，China

：ZHONG Qiu，Email：gdtb＠vip.163.com

ObjectiveTo utilize the metabolizing grey model to predict the trend of TB incidence and provide scientific evidence for formulating the related measures of prevention and control. Methods According to the incidence of pulmonary TB in the Guangdong province from 2001—2011，we established the conventional grey model［gray model（1，1），referred to as GM （1，1）］and the grey model of metabolism ［referred to as the metabolic GM（1，1）model］.We compared the precision and accuracy of model predictions by the results of short series and long series，then chose the best model for extrapolation forecast.The prediction accuracy can be showed by posterior error ratioCand small probability of errorP.The smaller class the best accuracy，fist class indicate the best and four failed.ResultsThe error of the grey model of metabolism is less in comparison with the corresponding dimensions of conventional grey model.The error is less in the shorter series prediction.The result of accuracy test showed that the 5-dimensional grey model of metabolism is in the first class.The model of posterior error ratio and small probability of error was 0.14and 1respectively. Conclusion The metabolic GM （1，1）is the ideal model to deal with such data，the five-dimensional metabolic GM （1，1）model has certain advantages to forecast the TB incidence in Guangdong province.

Tuberculosis，pulmonary／epidemiology； Incidence； Forecasting； Models，statistical； Tuberculosis，pulmonary／prevention ＆control； Guangdong province

国家“十二五”科技重大专项（2012ZX10004903）；广东省医学科学技术研究基金（C2010005）

510630广州，广东省结核病控制中心

钟球，Email：gdtb＠vip.163.com

2012-05-16）

（本文编辑：薛爱华）