基于可重构计算的纯方位目标要素解算方法

宋奂寰, 王树宗



基于可重构计算的纯方位目标要素解算方法

宋奂寰, 王树宗

(海军工程大学 兵器新技术研究所, 湖北 武汉, 430033)

目标运动要素解算所使用的数据处理技术的性能直接关系到潜艇作战系统的反应时间。目前, 对目标运动要素解算问题的研究多集中在改进或使用性能更优越的估计算法。本文在现有算法基础上, 利用可重构计算技术作为目标运动要素解算模块的加速器, 分析纯方位平差算法的输入数据流, 通过脉动阵列简化标量运算, 充分利用并行流水线机制, 最终实现了纯方位平差法的可重构计算。试验结果证明了使用可重构计算能够提高算法的解算速度。

纯方位目标; 运动要素解算; 可重构计算; 流水线; 脉动阵列

0 引言

目标运动要素解算是潜艇作战系统的核心任务之一。作战系统目标运动要素解算模块的功能是根据综合声纳、综合雷达系统的自动跟踪信息或手动输入的数据信息解算目标的运动参数,特点是该模块为数据密集型计算。目标运动要素解算所使用的数据处理技术的性能直接关系到潜艇作战系统的反应时间。一直以来, 对目标运动要素解算问题的研究多集中在改进已有的估计算法或使用性能更优越的估计算法, 使要素解算获得更好的收敛速度和解算精度, 例如最小二乘估计、扩展卡尔曼滤波、极大似然估计、而伪线性估计是其中的典型算法代表。

可重构计算是一种全新计算方式, 近年来随着微电子技术和计算机技术的发展, 可重构计算的研究条件日趋成熟, 国内外掀起了对可重构计算的研究热潮[1]。可重构计算使用集成了可编程硬件的系统进行计算, 该可编程硬件的功能可由一系列实时变化的物理可控点来定义, 其底层技术是现场可编程门阵列(field-programmable gate array, FPGA)技术[2]。以FPGA为先导的可重构计算技术的优点是, 硬件设计的实现基于软件的灵活性, 并且保持了传统的基于硬件方法的执行速度, 已经成为计算密集/数据密集型算法的加速器。本文基于可重构计算设计和实现目标运动要素的解算算法, 利用可重构计算的并行执行特性加速要素解算算法的解算速度, 利用可重构计算柔性重构特性, 提高算法精度。利用可重构计算系统开发应用的关键在于设计一套适合可重构计算系统实现的并行算法。本文以基于最小二乘估计的纯方位平差法为研究对象, 对于极大似然估计、扩展卡尔曼滤波、伪线性估计等算法同样可设计合适的并行算法, 在可重构计算系统上得到算法的加速实现。

1 纯方位目标运动要素解算问题描述

取北-东坐标系, 假设当本艇先后处于0,1, …,O位置时测得目标方位分别为0,1, …,b, 并记下各位置的对应时刻t和本艇位置坐标(x,y), Δt=t-t, Δb=b-b, Δx=x-x, Δy=y-y运用此算法可求得目标的运动参数。在目标匀速直线运动假定下, 由方位量测方程[3]

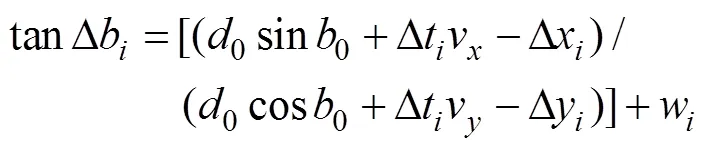
得到

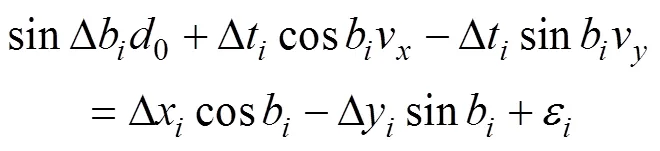
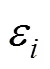
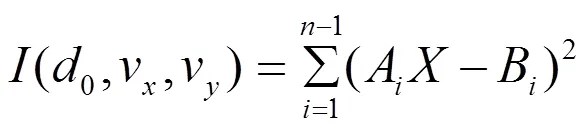
其中

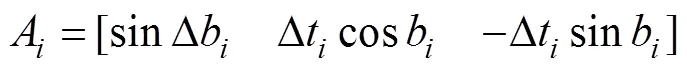
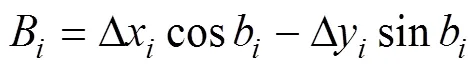
取待估计参数

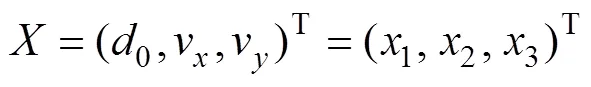
则基于最小二乘估计的目标运动要素解算问题就转化为对下述方程组的解算问题。

=(7)

其中

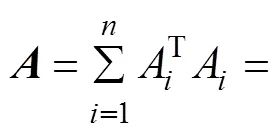
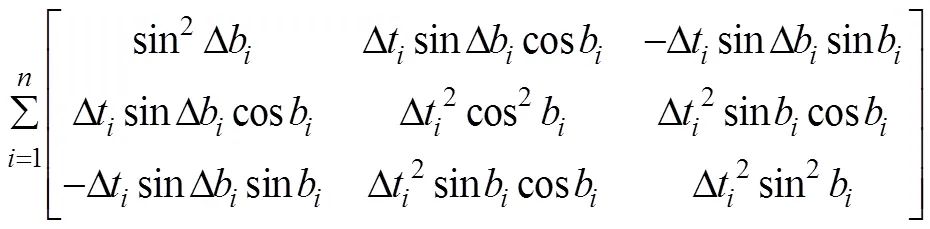
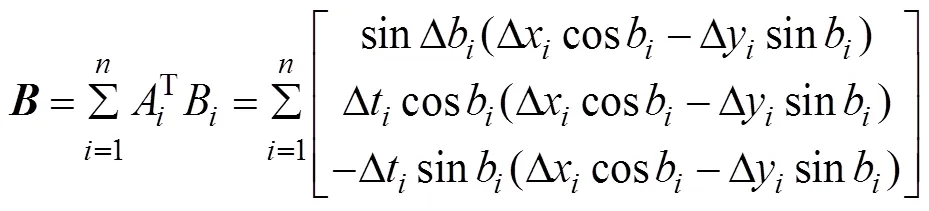
2 纯方位目标运动要素解算并行算法设计

利用可重构计算求解方程组=, 关键是把熟知的在通用处理器上串行执行的程序(如C语言程序)转换成适合于可重构计算系统的并行执行程序(如VHDL, Verilog语言程序), 这种转换需要首先设计出高效简洁的并行算法。但是, 最小二乘法需要在输入数据间进行大量运算, 而这不是目标运动要素解算问题所期望的, 因此, 并行算法需要简化对这些输入数据的计算, 以降低硬件设计复杂度和在不影响计算高效性的情况下, 使算法使用的可重构单元最少。引入通过分解得到的输入矩阵的直角三角形, 将系数矩阵转换为一个上三角矩阵, 可以消除输入矩阵的一些元素, 从而减少最小二乘法输入数据间的运算量[4]。

对式(7)进行如下变换(其中是酉矩阵,是上三角矩阵)

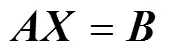
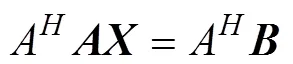
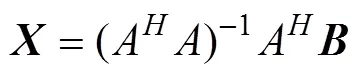
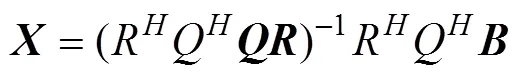
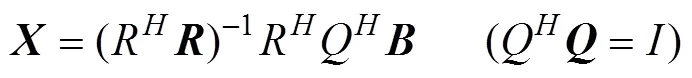
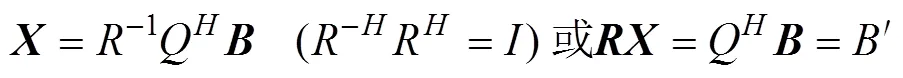
由于是一个上三角矩阵, 即

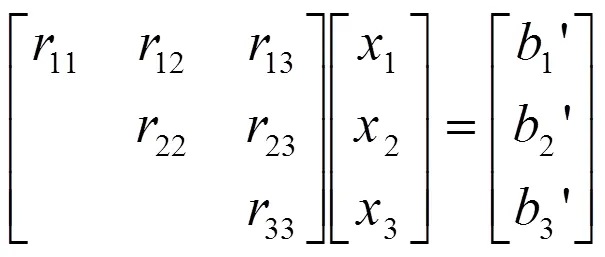
因此, 求解就只需进行下面的回代过程

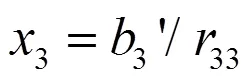
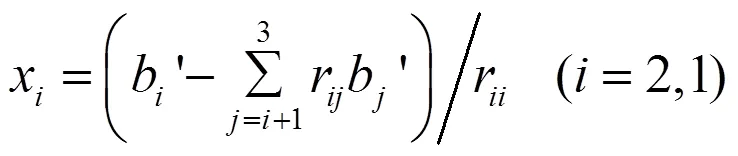
根据上述分析, 利用方程组=解向量就转换为利用方程组=¢解向量, 即对矩阵求其分解的矩阵(三角阵)和(酉矩阵), 其中¢=。这样的过程可以通过一系列Givens变换来实现。Givens矩阵是标准正交矩阵, 也叫平面旋转矩阵, 它是通过坐标旋转, 将元素的数值等效到元素上, Givens变换每次只能将一个元素变为0。Givens旋转的基本原理如下[4]

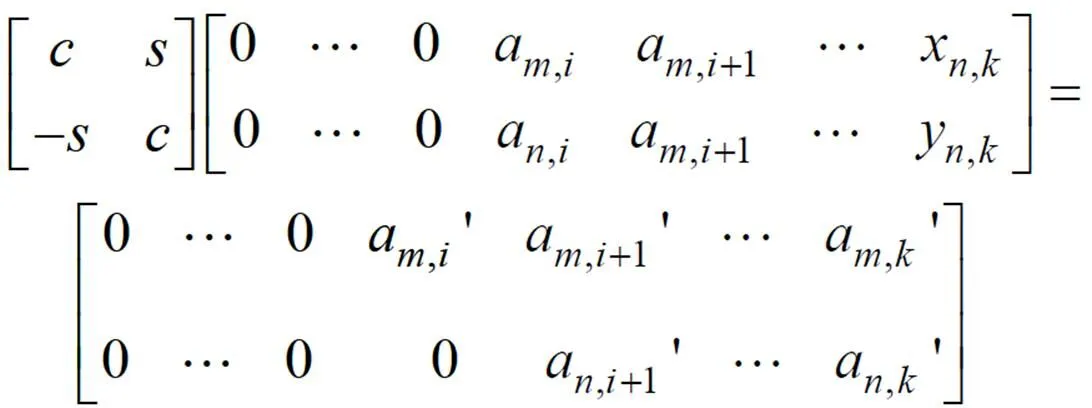
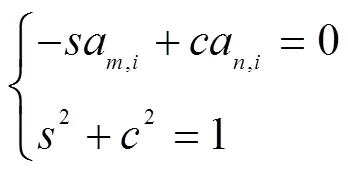
式(20)的一个解为

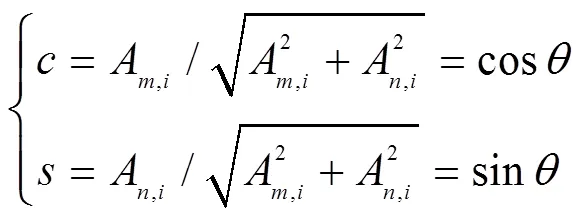
旋转后两行矩阵的新值为

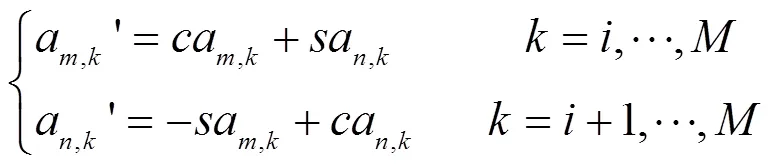
3 并行算法的可重构计算实现

脉动阵列可看成算法的硬件实现结构, 它把算法中包含的操作并行性用具有同样处理功能的处理单元通过简单和规则的通讯互联起来[5], 故脉动阵列很适合可重构计算系统设计。用脉动阵列实现方程组=到=¢的转化如图1所示。

脉动阵列由2种节点组成: 边界节点和内部节点, 它们对输入矩阵和输入向量的每个元素执行旋转操作, 滤去矩阵中的部分元素, 将矩阵转换为上三角矩阵形式, 对矩阵的元素进行旋转的目的是保证方程组等式成立(对执行某种变换, 对也需执行相同的变换)。

圆形节点为边界节点, 是对输入数据执行向量操作, 即将输入数据转化为旋转角度输出到内部节点(求解上文提到的Givens变换的旋转矩阵)。

方形节点为内部节点, 功能是利用来自边界节点的旋转角对输入数据进行旋转, 所得数据从上到下、从左到右传递 (执行上文所述Givens变换中矩阵乘法操作)。图中最后一列内部结点对方程组=等式右边的向量进行旋转, 更新向量的元素(执行上文所述Givens变换矩阵乘法操作)。

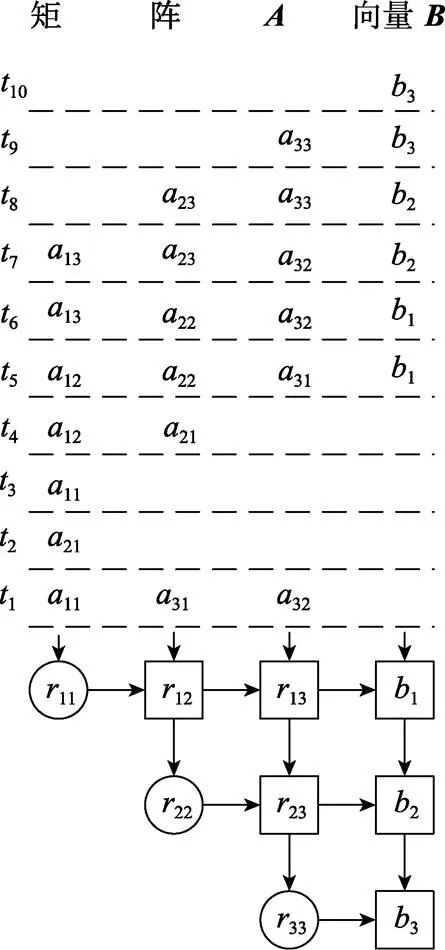
图1 纯方位目标运动要素解算的脉动阵列

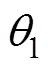
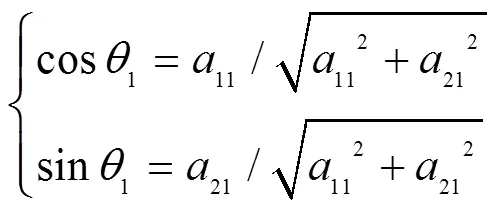
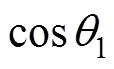
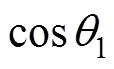
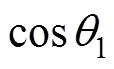
依次类推, 将式(24)的3个矩阵依次移入脉动阵列。若不计正/余弦函数的CORDIC解算时间, 转换3×3 D方程组到三角矩阵的形式只需15个处理周期。

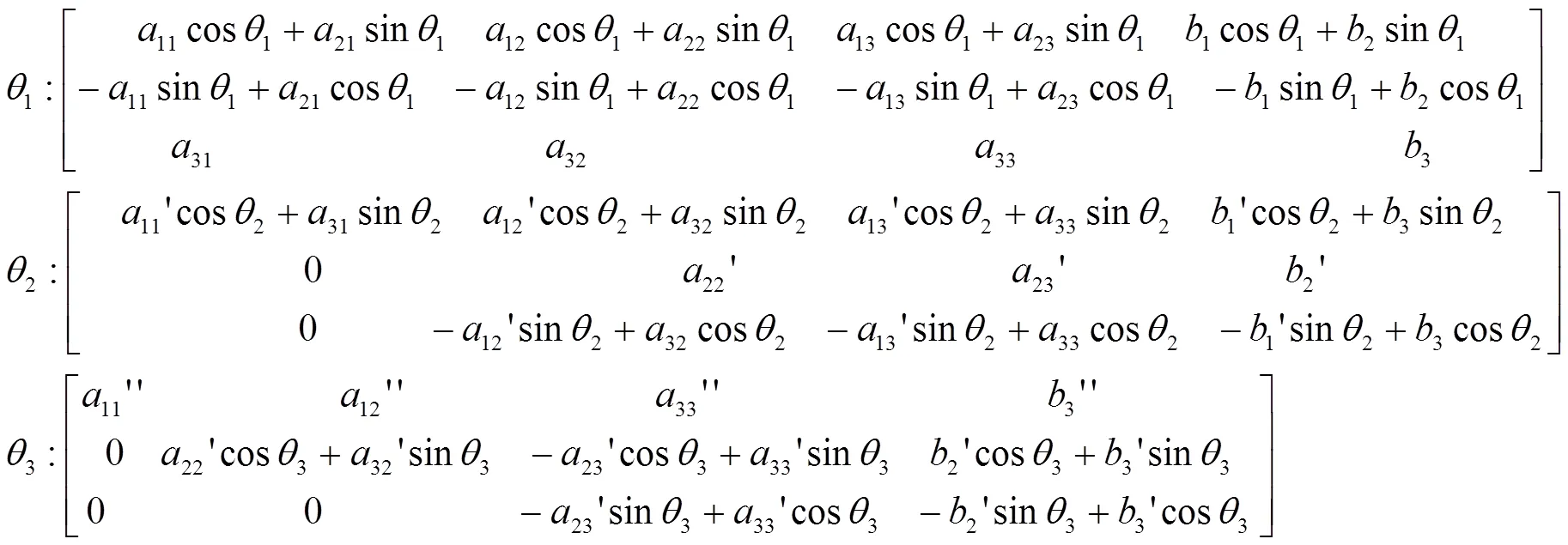
综上所述, 在可重构计算系统上实现了从方程=到=¢的转化, 下面介绍在可重构计算系统上求解向量的计算方法。

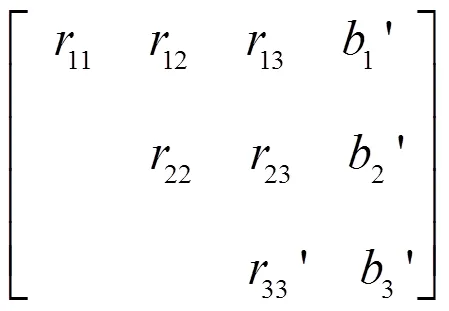
式(16)的整个求解过程从矩阵(25)右下角开始, 从下往上, 从左到右逐步展开。

1) 第1次迭代, 取第3列和第4列的元素

取33和3¢时, 经除法运算得到

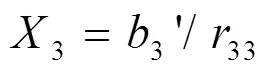
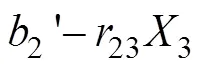
2) 第2次迭代, 取第2列的元素

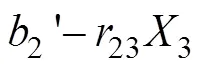
3) 第3次迭代, 取第1列的元素

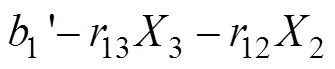
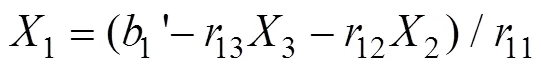
在可重构计算系统上实现上述迭代计算需要进行乘法操作、除法操作和减法操作, 另外还需要存储器和寄存器存放输入的方位信息数据和解算过程的中间结果, 多路选择器用于对多组输入数据进行选择性输出。在可重构计算系统上实现回代法解线性方程组, 只有在输出稳定后才能输入新的数据进行下一次计算, 即算法的节拍必须大于运算电路的延迟, 但如果采用流水线, 就有可能将一个操作分解为一些小规模的基本操作, 将中间值存储在寄存器中, 并在下一个处理周期内继续运算, 这样就可以提高电路的利用效率。如图2所示, 使用了两个触发器实现流水线结构。只需6个处理周期就可完成方程组的迭代求解。

图2 流水线实现线性方程组的回代求解

Fig. 2 Pipeline back substitution to realize linear equations

4 试验与算法性能分析

为了证明可重构计算系统可以作为目标运动要素解算模块的加速器, 本文设计选用Xilinx公司的Vertex-4 SX35, Vertex-4 SX35器件。

1) 使用的参数见表1。

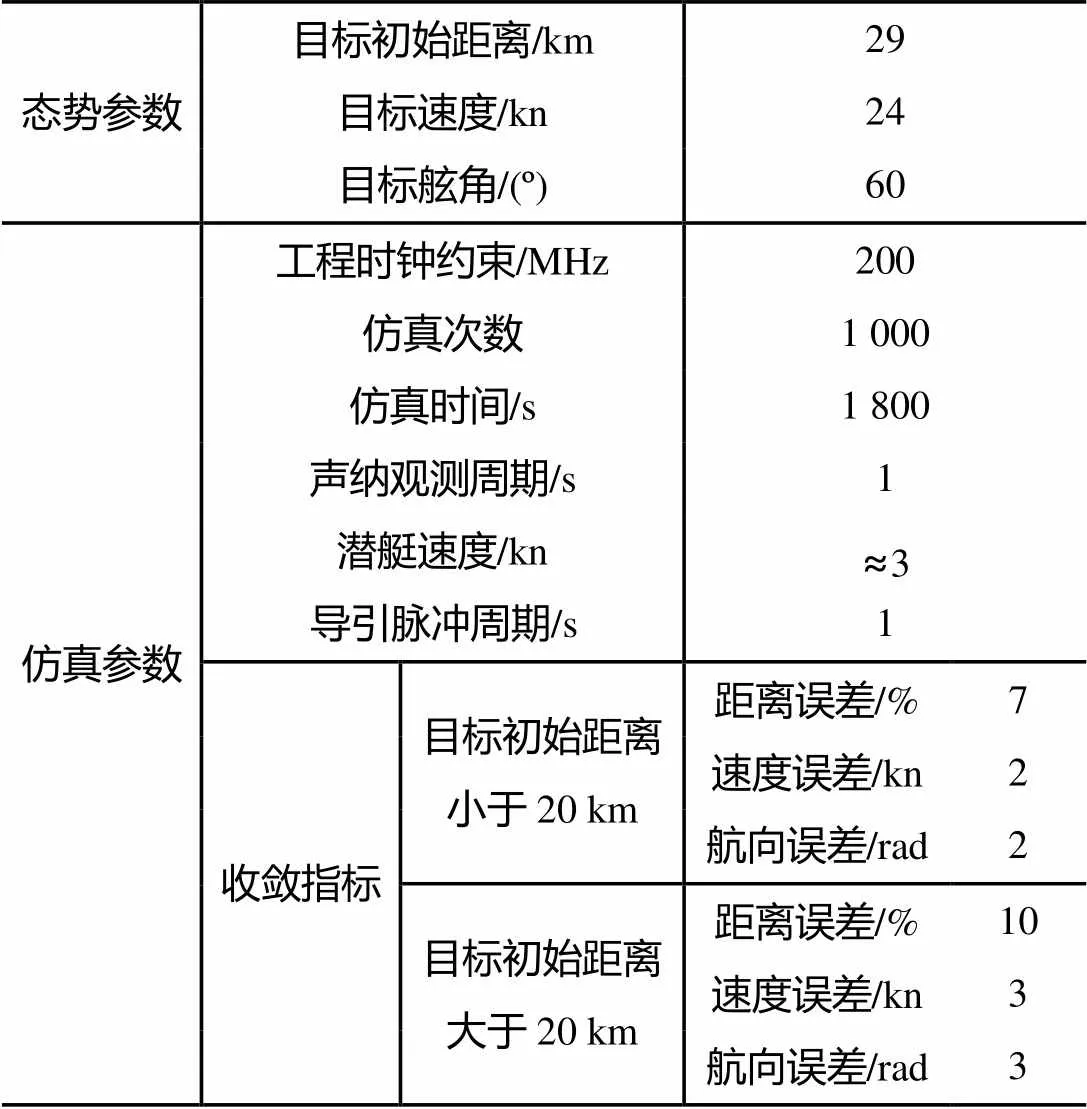
表1 仿真参数

2) 态势仿真及试验数据获取。根据表1描述的参数, 生成作战态势仿真如图3所示, 仿真显控台上直线航迹是目标航迹, 折线航迹是我艇为使纯方位平差算法收敛而采取的本艇机动航迹。对该固定态势进行要素解算, 声纳系统获得的目标方位变化率如图4所示。

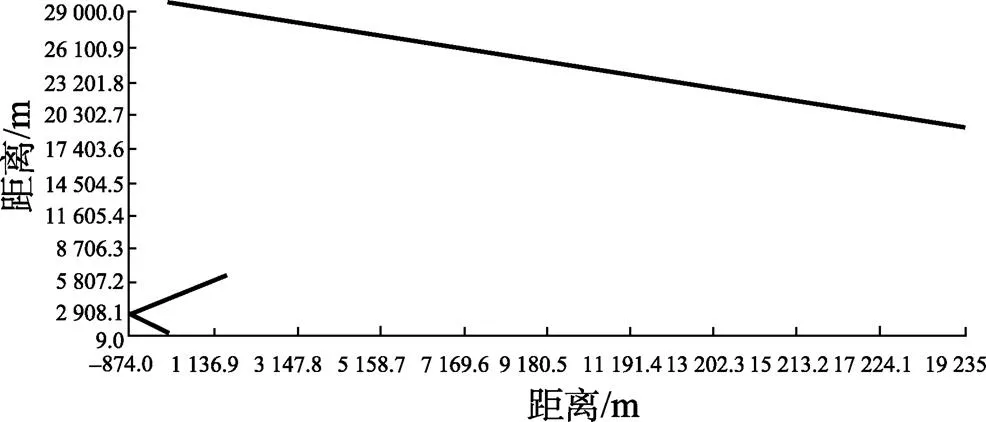
图3 态势图

记录每一时刻我艇位置、推算的目标位置、声纳探测的目标方位数据, 作为输入信息加载到Vertex-4 SX35器件的Block RAM存储器。

3) 试验结果及性能分析

整个并行算法所使用的可重构单元、布线资源等资源如表2所示。该设计吞吐量为0.13 M/s, 通过流水线设计, 吞吐量提高到0.15 M/s。生成上三角矩阵的时延为777个处理周期, 回代过程耗费156个处理周期。在实艇装备中, 不考虑传感器系统的处理瓶颈, 在普通台式机上, 利用VC++平台运行程序目标运动要素解算模块的仿真程序, 耗时约125000ns, 因此, 可重构计算系统可以使目标运动要素解算模块执行速度提高约14.9%。

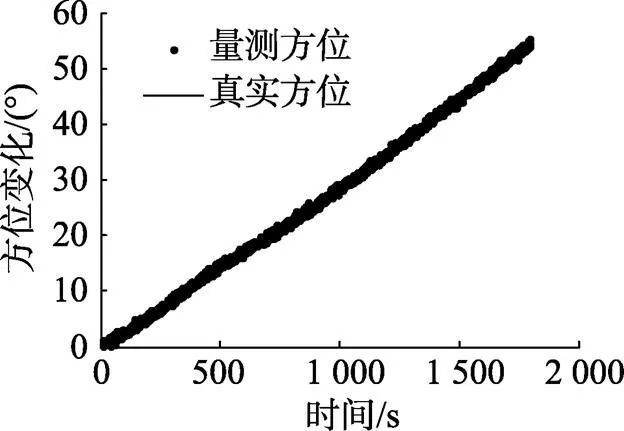
图4 量测方位信息图

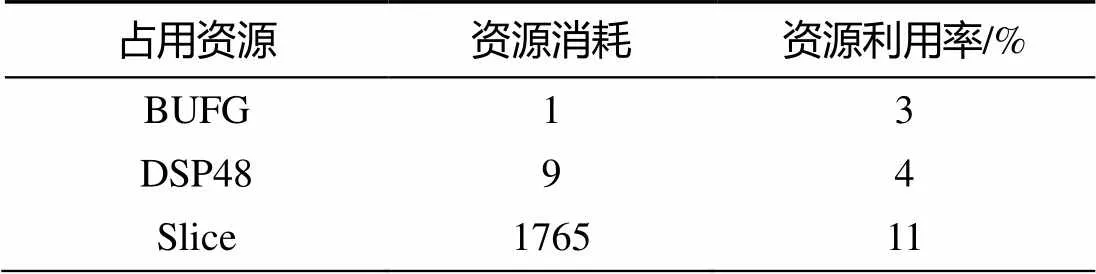
表2 资源占用情况及试验结果

注: 时钟频率: 200 MHz; 时钟周期: 368；消耗时间: 1840 ns

5 结束语

本文通过研究基于最小二乘估计的纯方位平差算法, 设计了专用的运算单元, 充分利用并行机制, 在Vertex-4 SX35器件上实现了纯方位平差算法, 试验结果证明了设计合理的并行算法, 利用可重构计算可以提高目标运动要素解算模块的执行速度。

[1] 王志远, 王建华, 余旸. 可重构计算综述[J]. 小型微型计算机系统, 2009, 30(6): 1203-1207.

Wang Zhi-yuan, Wang Jian-hua, Yu Yang. Reconfigurable Computing Summarizing[J]. Journal of Chinese Computer Systems, 2009, 30(6): 1203-1207.

[2] Compton K, Hauck S. Reconfigurable Computing: A Survey of Systems and Software[J]. ACM Computing Surveys, 2002, 34(2): 171-120.

[3] 李洪瑞. 水下目标运动分析关键技术研究[D]. 南京: 南京理工大学, 2009: 16-30.

[4] Xilinx. AccelWare Reference Designs User Guide[M]. China: Xilinx, 2009.

[5] H T, W M. Matrix Trangularization by Systolic Arrays[C]// Proceedings of the Meeting, United States, 1981.

Bearing-only Target Motion Elements Solver Based on Reconfigurable Computing

SONG Huan-huan, WANG Shu-zong

(Naval Research Institute of New Weaponry Technology and Application, Navy University of Engineering, Wuhan 430033, China)

Reaction time of submarine combat system depends on data processing technology used in target motion elements solver. Based on existing algorithms, reconfigurable computing system is taken as accelerator of target motion elements solver to analyze the input data stream of bearing-adjustment algorithm, and simplify scalar operation of systolic array. Reconfigurable computing of bearing-adjustment algorithm is implemented by using pipeline parallel principle. Experimental results verify that reconfigurable computing can accelerate execution speed of the algorithm.

bearing-only target; motion elements solver; reconfigurable computing; pipeline; systolic array

E925.66; O141.4

A

1673-1948(2012)03-0236-05

2012-01-10;

2012-02-22.

国防973项目(613660202); 中国博士后科学基金项目(200902668).

宋奂寰(1983-), 女, 在读博士, 主要研究方向为潜艇作战系统目标跟踪.

(责任编辑: 许妍)