桥梁结构监测数据预处理方法及其应用

雷旺龙，孙洪鑫，郭雪涛

（湖南科技大学 土木工程学院，湘潭 411201）

0 引 言

随着交通运输的发展，作为发挥重要作用的桥梁的健康状态已经越来越多地受到大家的关注，尤其是运营阶段的桥梁，在日积月累的荷载的作用下，以及周围环境的影响，桥梁结构的刚度会逐渐下降，承载能力也随之降低.为了保障桥梁结构的安全运营，有效防止灾难的发生，很多大跨度桥梁相继安装了桥梁健康监测系统［1］，通过对桥梁荷载、响应、几何、以及桥梁的辅助设施等［2－4］的监测所获得的数据，可以实时地了解桥梁的安全状况，然而随着监测系统的不断增多，由其产生的大量监测数据进行有效合理的的分析处理显得尤为重要，只有准确的数据分析才可能为已建桥梁的状态评估提供可靠的依据.

本文以已经正常运行两年多的九江大桥健康监测系统为背景，对其采集的数据中存在的粗差问题，采用粗差剔除方法中两种合理的方法进行必要的预先处理，并对噪声数据进行平滑处理，最后对所采取的处理方法进行比较分析.结果表明通过预处理的监测数据为桥梁的健康状态评估［5－7］提供了有效的基础数据.

1 数据预处理方法

通过健康监测系统可以获得大量的监测数据，以为桥梁的状态评估服务，然而采集中难免有出现异常的粗大误差数据以及由外界因素干扰而产生的噪声数据等.如果把这些数据也录入到数据库中，首先对桥梁性能的评价毫无意义，其次还会造成数据库运行效率大大降低，无法发挥软件处理海量数据以提高效率的优越性，因此需要对数据进行处理.

1.1 粗大误差数据的处理方法

粗大误差剔除的处理方法有拉依达法则、肖维勒准则、格拉布斯准则、狄克逊准则［8］以及数据跳跃法［9］等.

（1）拉依达准则

根据统计理论，在任意有限的多次测量列中，测量值的算术偏差ΔXi＞3σ的可能性小于1%，若出现了就可把它视为粗大误差，并将其对应的测量值从测量列中剔除，对于一个测量列中，可能不止一个粗大误差，所以每剔除一个之后，要再求剔除之后数列的均方差σ，再判断其值是否满足拉依达法则，若不满足则应该将该测量值剔除，如此反复计算直到无粗大误差为止.

（2）肖维勒准则

肖维勒准则针对不同的测量次数n，规定了不同的置信区间，肖维勒规定的这个置信区间的置信度为设该置信区间误差的极大值为ΔXmax，则由误差分布函数替换有式中t＝hΔXmax／σ，对给定的n，由积分表查出t值，计算出ΔXmax／σ，对不同的n，ΔXmax／σ的相应值如表1所示.剔除的方法与拉依达方法类似，仅只是极限误差的定义不同.肖维勒准则的极限误差为aσ，其中a为极限误差系数，凡大于aσ的误差应视为粗大误差，而把它剔除.

表1 误差限值表

（3）格拉布斯准则

在测量数列中，应用格拉布斯准则判断数据是否有粗大误差时，首先计算样本标准偏差σ和平均值，之后计算判断统计量，其次格拉布斯系数λ可根据显著度a和观测次数查表2得到.如果某个测量值的残余误差的绝对值Vi满足｜Vi｜＞λ（a，n）σ，则认为Vi对应的观测值为粗大误差，应该予以剔除.

表2 格拉布斯系数表

（4）狄克逊准则

狄克逊检验法需设置显著性a，通常设显著性水平a＝5%，作为判断是否有异常值的水平，当判断存在异常值之后，采取有效的措施消除异常值.若无法查明其中的原因时，应设a＝1%为剔除水平，判断该异常值是否应当从数据中剔除.当判断为异常值而又达不到剔除水平时，应以剔除和不剔除的两种统计结果相比较，看哪种结果更接近实际情况.当给显著性水平和剔除水平后，从相应的临界值表3中查得临界值与所计算的统计量D相比较，做出判断和剔除的决定.

统计量的计算：

①当对最小值进行判别时

②当对最大值进行判别时

表3 狄克逊临界值表

（5）数据跳跃法

在采用拉依达法则进行剔除监测数据中的粗大误差数据时，发现拉依达法则程序每运行一次只能剔除一个粗差，当有多个粗大误差时会需要很长的运行时间，并且多个粗差之间互差不满足一定条件时拉依达法则失效.采用改良后的数据跳跃法将监测值由小到大排列，则含有粗大误差的监测值一定分布在两侧，粗差存在的位置出现跳跃现象，在跳跃点处将数据分为两段，第一次将首个跳跃点及其平缓的监测值组成一组数列，利用拉依达法判断跳跃点是否为含有粗差的监测值，如果它不是，可将跳跃点后的第一个监测值和之前的监测值组成一组数列，并利用拉依达法判断该跳跃点是否为含有粗差的监测值，如果不是，同样方法继续进行下一步判断直至这一侧拥有最大残差的监测值，则这一侧的其他各观测值均为含有粗差的观测值，都应被剔除.利用数据跳跃法进行粗差剔除，它克服了拉依达法则的部分局限性，同时可以将含有多个粗差的监测数据进行批量剔除，从而大大提高剔除粗差的效率.

其中拉依达法则及数据跳跃法适用于大量数据的粗差剔除处理分析，而肖维勒准则、格拉布斯准则以及狄克逊准则多用于小样本的粗差分析，如桥梁健康监测中监测周期相对较长而获得的少量数据.

1.2 噪声数据平滑方法

由健康监测系统采集的大量数据，基本都是所期望得到的真实值和外界各种干扰等噪声一起的叠加数据，为了获得真实值，采取一定的数据平滑方法有效消除噪声，以方便对结构的健康状况得到更直接的了解.

数据平滑的方法有：

（1）移动平均法（Moving Average）：采用移动平均值进行替换原始数据以达到消除噪声的目的.当移动平均时距项数N为奇数时，只需一次移动平均，其移动平均值作为移动平均项数的中间一期的代表值；而当移动平均项数N为偶数时，移动平均值代表的是这偶数项的中间位置的水平，无法对正某一时期，则需要在进行一次相临两项平均值的移动平均，这才能使平均值对正某一时期.

（2）局部加权回归散点平滑法（locally weighted scatterplot smoothing，LOWESS）：

局部加权散点图平滑数据，采用线性最小二乘法和一阶多项式拟合得到的数据替换原始数据的方法.平滑后曲线的光滑程度与所选取的局部数据比例有关，比例越少，拟合越不光滑，反之越光滑.

（3）局部修正平滑数据法（locally weighted scatterplot smoothing，LOESS），采用线性最小二乘法和二阶多项式拟合得到的数据据替换原始数据的方法.该方法与局部加权回归散点平滑法类似，都适用于局部数据平滑，区别在于曲线拟合阶次不同.

（4）Savitaky－Golay平滑法（Savitzky－Golay Smoothing Filters）：采用未加权的线性最小二乘法过滤数据，利用指定阶数的多项式拟合得到的数据替换原有数据的方法.该方法可以有任意的步长，应用较方便灵活.

各种数据平滑方法根据工程具体情况合理选择应用.

2 数据处理方法应用

本文以已经正常运行两年多的广东九江大桥健康监测系统为背景，采用前文所述的数据处理方法对采集系统所获得的数据进行预处理分析.

2.1 九江大桥健康监测系统

九江大桥为单箱四室梁身结构的斜拉桥，自1988年6月建成通车以来，至今已运营23年多，为了对桥梁的健康状况得以很好把握，2009年开始给桥梁安装了健康监测系统，该系统在主梁的6个代表性的截面上分别安装了振弦式应变计，其中每个截面分别在其底部表面安装5个应变计，共30个应变计用以对主梁的应变进行观测，同时为了获得斜拉桥重要构件斜拉索的索力数据，在144根拉索中按照优化布置原则选择每个索面布置9个，共安装了36个穿心式索力传感器，所安装的每种传感器同时具备温度采集功能，通过这些传感器系统以及信号采集与传输系统可以获得桥梁的关键部位及构件的实时状态数据，以为桥梁的状态评估服务.

2.2 拉依达法则与数据跳跃法应用分析

由于九江大桥健康监测系统每20min自动采集一次数据，产生了大量的数据，所以选用适合于大量数据处理的拉依达法则及数据跳跃法对数据中的粗差的进行剔除处理，并对两种方法所获得的结果进行分析比较.

由于篇幅原因，本文选取九江大桥2010年5月25日索力计采集的ZA8索力数据为例分析说明如下：

图1 粗差剔除对比图

图1所示的索力的平均值为1985.6kN，其3倍均方差为217.65，按照拉依达法则，图1中的最大误差217.6小于3倍均方差，所以没有数据被剔除，但是最大误差严重偏大，这种误差很明显很不理想；但采用数据跳跃法则很好的解决了这个问题，处理后的数据均方差为7.61，其精度比采用拉依达法则提高了9倍多，使得处理后的数据有效性更高，同时拉依达法则程序每运行一次只去掉一个粗差，多个粗差的剔除需要时间较长，数据跳跃法因为只需判断首个临界粗差值，对大于临界值的粗差一次性剔除，运行速度较快.

2.3 数据平滑方法的应用分析

本文对经过粗大误差剔除处理的ZA8索力数据进行平滑处理，其对比结果如图2所示.

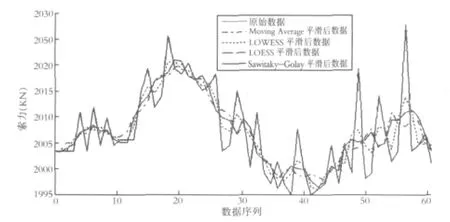
图2 平滑处理索力ZA8前后数据对比曲线

由图2可知，经过平滑处理的数据明显比原始数据光滑很多，通过这种方法可以很好的剔除噪声数据，使得有效数据得以保留.但各个数据平滑方法的平滑程度以及平滑优势各不相同，应根据工程实际合理选择应用.

3 结 论

本文通过对桥梁监测数据预处理中粗大误差剔除方法以及噪声数据的平滑方法的总结与应用分析得出以下结论：

（1）对不同的桥梁监测数据应选用不同的数据预处理方法，如对采集频率高所获得的大量数据可选用拉依达法则或者数据跳跃法进行粗差分析，对于采集周期较长所获得的少量数据可选用肖维勒准则等.

（2）数据跳跃法对桥梁监测数据粗大误差的剔除更加合理高效.

（3）对桥梁监测数据采用合理的平滑处理方法可以很好的处理噪声数据，以满足结构状态评估所需的有效数据.

［1］Wang K Y，Chan W Y K，Man K L.The Use of Struc－tural Health Monitoring System in Operation ＆ Maintenance of Cable－supported Bridges［A］.In：One Day Annual Sdminar Structural Symposium 2000Highway and Railway Structures［C］，Hong Kong，2000.

［2］黄方林，王学敏，陈政清，等 .大型桥梁健康监测研究进展［J］.中国铁道科学，2005，26（2）.

［3］李 惠，欧进萍.斜拉桥结构健康监测系统的设计与实现（I）系统设计［J］.土木工程学报，2006，36（4）.

［4］邬晓光，徐祖恩.大型桥梁健康监测动态及发展趋势［J］.长安大学学报，2003，23（1）.

［5］段香英，王 乐.桥梁评估方法研究［J］.公路工程与交通，2004，134（10）.

［6］袁万城，崔飞，张启伟.桥梁健康监测与状态评估的研究现状与发展［J］.同济大学学报，1999，27（2）.

［7］李宏男，李东升.土木工程结构安全性评估、健康监测及诊断述评［J］.地震工程与工程振动，2002，22（3）.

［8］郑叔芳，吴晓琳.机械工程测量学［M］.北京：科学出版社，1999.

［9］毛亚纯，王恩德，修春华.剔除变形监测粗差数据的新方法－数据跳跃法［J］.东北大学学报（自然科学版），2011，32（7）.