考虑最低允许质量水平的逆向物流生产库存模型及其粒子群算法

陈 铓，龚存宇

（湖南工程学院 机械工程学院，湘潭 411101）

0 引 言

对旧产品进行回收并循环利用能够减少废弃物数量，保护自然环境，同时企业也可以通过回收旧产品再生利用在经济上得到收益，故近年来各界对进行产品回收再制造也就是逆向物流管理更加关注.Dobos［1］指出逆向物流管理即是将已使用过的或者可重复使用的零件和产品从客户处回收到生产者进行再处理.大多数逆向物流库存模型一般假设回收产品的质量水平符合再制造的要求，然而现实的逆向物流系统中回收产品的质量水平确实参差不一，需要进行检验才能决定再处理的方式.Salameh［2］研究了所有回收的旧产品在全数检验完成后，将其中的不良品以低价卖出为原则的逆向物流库存问题，假设不允许缺货且补货为瞬间完成.Papachristos［3］以Salameh模型为基础，对不允许缺货发生的库存模型进行最优经济订购量求解，其中假设不良品是在检查完毕后直到订购量用完后才进行销售.Eroglu［4］则依循先前的方法并增加了允许缺货的条件.

Chan等人［5］亦对此问题进行研究，发现回收产品的不良率越高，所需要对外订购的新产品的批量也越大.Porteus［6］认为回收产品的质量与再制造批量之间存在着显著关系，即在给定的概率下，回收产品的批量足够大就会出现不良品，如此再制造系统便会因为重工等相关的操作而发生额外的费用.Porteus提供了三项生产质量改善的方法，即降低过程失控的机会、降低固定成本以及同时使用上述两种方法.Lee［7］将生产的时间长度视为决策的主要因素，并强调用检验的方式进行质量控制以建立EPQ模型.

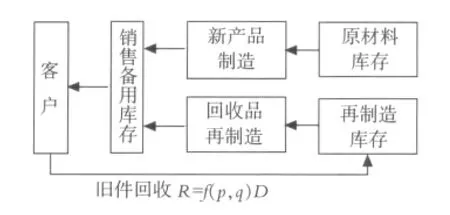
图1 逆向物流库存系统

本文以Salameh模型为基础提出如图1所示的逆向物流生产库存系统，其中只有那些满足最低质量水平的已使用过的产品才被允许从客户处购买回来供再制造，但是由于回收产品的质量参差不齐，所以将质量水平作为随机变量处理，研究目标是最小化平均总库存成本.

1 符号定义与假设

1.1 符号定义

（1）决策变量

T：一个制造与再制造周期的时间长度；

P：回收产品与新产品的价格比（0≤P≤1）；

q：允许的最低质量水平（0≤q≤1）；

（2）输入参数：

a，θ：价格函数的参数（0≤a≤1）；

b，Φ：质量函数的参数（0≤b≤1）；

c，δ：再制造成本函数的参数；

hS：单位时间销售备用品的库存持有成本；

hR：再制造产品的库存持有成本；

hraw：外购原材料的库存持有成本；

CM：单位制造成本；

（1／γ）D：再制造的速率；

（1／β）D：制造的速率；

SR：再制造的准备成本；

SM：制造的准备成本；

D：需求率；

Pn：产品的销售价格；

Craw：原材料的单位购买成本；

Co：有原材料的订货成本；

（3）模型参数：

R：回收产品的数量；

CR：再制造的单位成本；

HS，1：新制造产品在销售备用仓库存储时平均库存成本；

HS，2：再制造产品在销售备用仓库存储时平均库存成本；

HR：再制造存货的平均库存成本；Hraw：原材料的平均库存成本；

1.2 模型假设

假设无限计划期内客户需求是稳定的，为已知的常数，由制造和再制造产品共同满足.回收率是回收产品的质量水平和单位回购价格的函数，即旧产品的回收率取决于最低允许的质量水平以及回购价格与新产品价格的比例.只有那些满足最低质量水平的旧产品才被允许从客户处购买回来以供再制造，但是由于回收产品的质量参差不齐，所以将质量水平作为随机变量处理，假设回收产品的质量水平服从均匀分布.回收产品将由再制造库存转移到再制造环节，所有回收的产品均进行再制造，再制造产品的质量与新生产的产品是相同的，另外再制造的单位成本依赖于回收产品的质量水平.再制造产品被存储在销售备用仓库中，假设库存容量是无限的.由于假设不允许缺货发生，新产品必须是新制造的并储存在销售备用仓库中以满足市场需求.在新产品制造中，从外部供应商订购原材料采用经济订购批量（EOQ）.另外假设每个周期中新品制造与回收品再制造均为单一批次，即一个周期内仅进行一次制造和再制造作业.

2 库存模型的建立

2.1 回收率函数

假设旧产品的回收数量R是价格因素与质量因素的函数，本文采用 Vörös［8］提出的需求函数进行修改，同时假设这两个因素是相互独立的.质量因素是指生产厂家为再制造作业规定的回收产品的最低允许质量水平，质量函数为fq＝beφq.价格因素是指旧产品的回购价格与新产品的价格之比，价格函数的数学形式为R＝R（p，q）＝D（1－αe－θp）be－φq.于是旧产品的回收率函数为

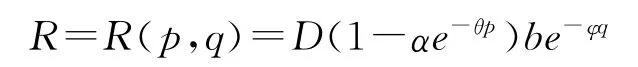
2.2 各类存货的库存持有成本

以回收产品的库存水平下降至零为节点，定义T为两个相邻节点的时间间隔，表示为周期时间长度.再制造需要的时间为TR，新产品制造需要的时间为TM，于是T＝TR＋TM.本文提出的逆向物流生产库存系统中有三种不同的存货，即再制造库存、销售备用库存和原材料库存（如图2所示）.

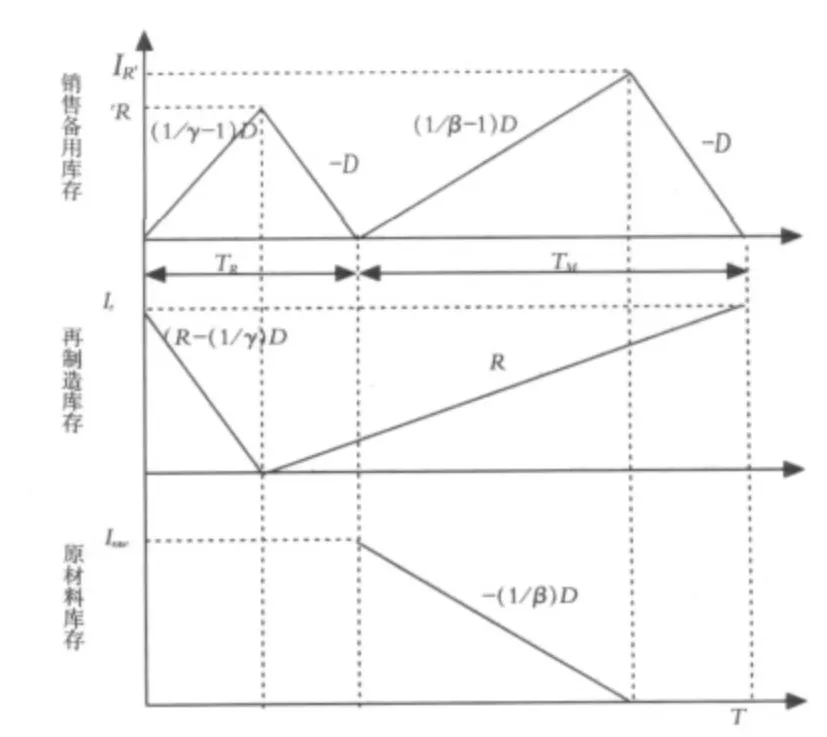
图2 三种存货的库存水平

（1）新产品的销售备用库存的平均库存成本

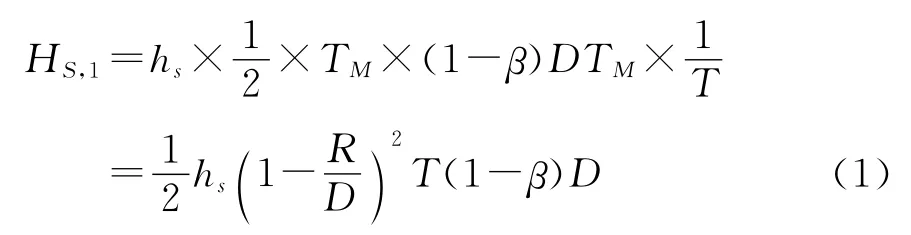
（2）再制造产品的销售备用库存的平均库存成本

（3）再制造库存的平均库存成本

（4）外购原材料的平均库存成本

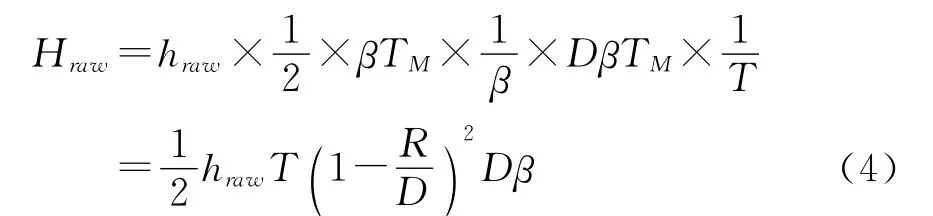
2.3 系统的平均总库存成本

逆向物流生产库存系统的平均总成本包括平均库存持有成本、平均设置成本、平均订购成本、平均再制造成本、平均生产成本、平均采购成本和平均回购成本.

（1）平均库存持有成本

平均持有成本是方程（1）至（4）之和.

（2）再制造和制造的平均设置成本

（3）原材料的平均订购成本

（4）平均再制造成本

平均再制造成本是预期再制造的成本乘以旧产品的回收数量.

其中CR＝ce－δx

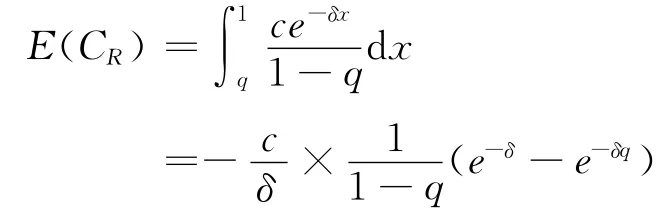
（5）平均制造成本

平均制造成本等于再制造产品不能满足的需求的数量乘以单位制造成本

（6）平均原材料成本

根据公式（9），原材料所需的材料平均金额可以表示为

（7）平均回购成本

回购成本等于从客户回购旧产品的价格乘以数量

（8）平均总库存成本

逆向物流生产库存系统的平均总成本可以表示为

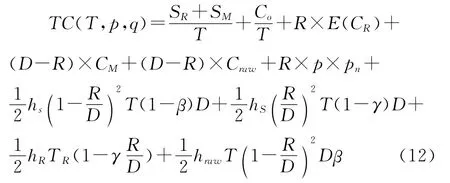
假设P和Q为已知数，对上式取T的一阶、二阶偏导数

由于SR，SM，CO，T均为正数，所以二阶偏导数值大于零.由于p、q为已知值，TC在T为凸，令一阶偏导数为零求解T，即可得到T的最优值

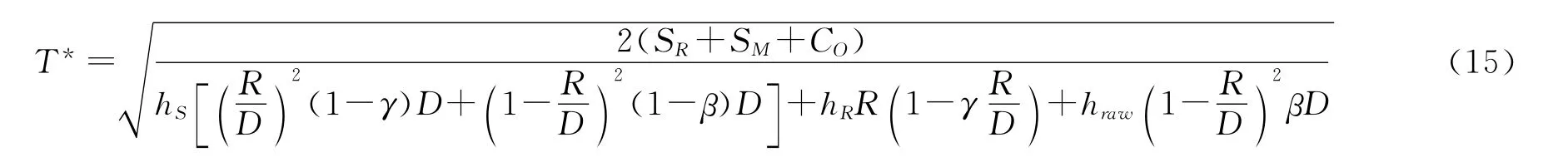
3 模型求解与数值算例

在上节建立的逆向物流生产库存模型中有三个决策变量，即实数T、p和q，其范围在0～1之间.由于目标函数的数学复杂性，因此本文提出了基于粒子群优化的启发式算法.

3.1 粒子群算法

粒子群优化算法（PSO）是一个连续的非线性函数的优化方法.Kennedy［9］使用鸟群和鱼群的比喻介绍了这种方法.粒子群算法是受个人之间的社会行为的启发，这些人（我们称之为粒子）在整个n维搜索空间运动，每个粒子代表一个问题的潜在解决方案.所有的粒子可以分享他们对搜索空间的信息，这样他们就可以得到全局最好的解决办法.在每次迭代中，每个粒子的速度根据给定的算法更新和计算.

粒子群优化算法如下：

步骤1初始化一个随机事件的立场和对p－q的粒子尺寸速度阵列.

步骤2计算T＊.

步骤3在搜索空间计算每个粒子的TC.

步骤4检查是否符合停止运算的标准.如果符合标准，即停止，否则转到步骤5.

步骤5更新每个粒子的pbest值和gbest值.

步骤6使用pbest，gbest和以前的速度更新每个粒子的位置.

步骤7转到步骤2.

3.2 数值算例

本文使用C＋＋编程对提出的启发式算法性能进行了测试，并通过网格搜索方法得到次优解.测试问题的参数值为：hS＝4，hR＝3，hraw＝1，CM＝30，SR＝5000，SM＝5000，D＝1000，Pn＝100，Craw＝20，Co＝1000，a＝0.9，b＝0.9，γ＝0.6，β＝0.5，δ＝1.对于三个不同的θ和Φ值，一共有9个算例.

表1 粒子群启发式算法的性能

0.01 1 0.7 0.06 0.51 20.76 2009.24 18755.03 48534..51 ＜0.01 1 0.04 0.20 20.42 2052.54 18379.30 48709.83 ＜0.01 2 0.05 0.16 20.80 2003.82 18803.24 48976.82 ＜0.01 2 0.06 0.11 17.02 2599.64 14421.37 48483.73 ＜

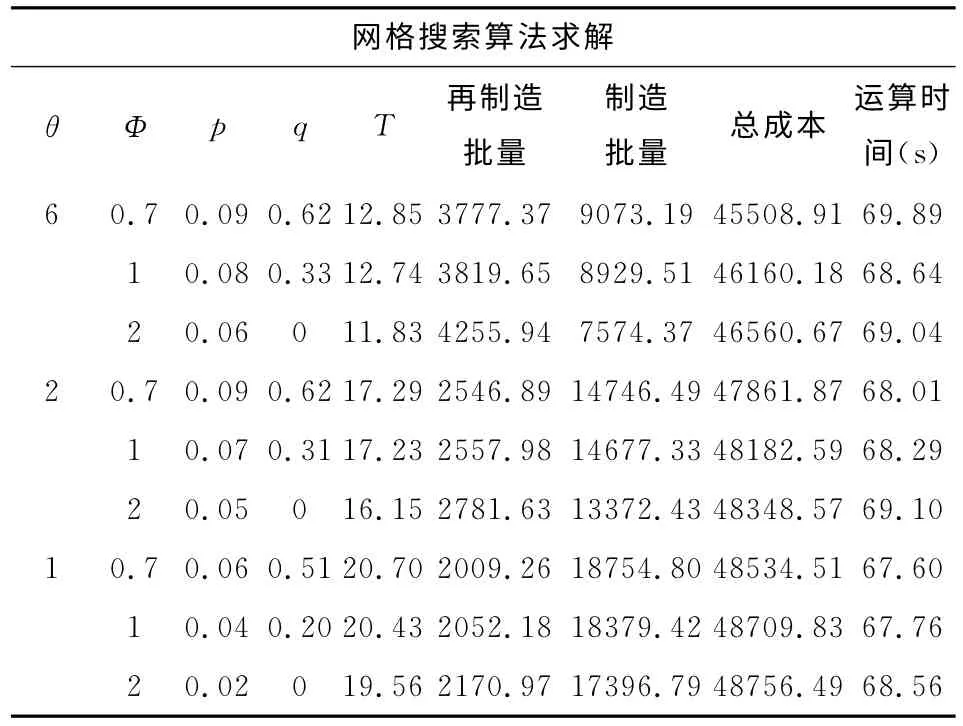
表2 网格搜索算法的性能

如表1、表2所示，在所有情况下粒子群优化算法的计算时间小于0.01s，然而网格搜索算法的计算时间超过1min.

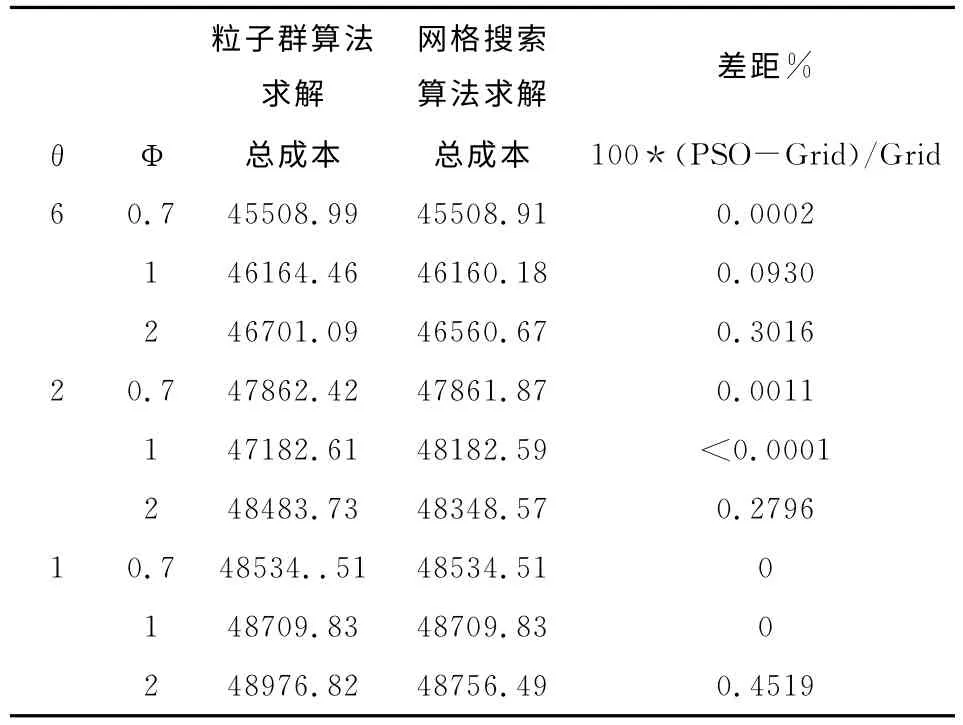
表3 PSO与网格搜索算法的性能对比

如表3所示，基于粒子群的启发式算法的性能与网格搜索算法一样良好，即次优解的最大差值为0.4519%.因此，本文提出的算法可以在很短的时间内得到次优解.

4 结 论

本文对以再制造与新制造产品共同满足固定需求的逆向物流生产库存系统进行了研究.本文引入在以往文献中被忽略的但是在现实世界中很重要的最低允许质量水平的概念，假设旧产品的回收率是质量水平与单位回购价格的函数，以此变量建立了库存成本函数.由于逆向物流库存模型的复杂性，本文提出了粒子群优化算法去求解该模型.为了检验粒子群算法的性能，本文将该算法得到的次优解与网格搜索方法进行了比较，结果发现该算法与网格搜索方法得到相同结果的时间基本相同，由此证明了本算法的有效性.

［1］Dobos I.，Richter.An Extended Production／Recycling model with Stationary Demand and Return Rates［J］.International Journal of Production Economics，2008，90（3）：311－323.

［2］Salameh M.K.，Jaber M.Y.Economic Production Quantity Model for Items with Imperfect Quality［J］.International Journal of Production Economics，2000，64：59－64.

［3］Papachristos S.，Konstantaras I.Economic Ordering Quantity Models for Items with Imperfect Quality［J］.International Journal of Production Economics，2006，100：148－154.

［4］Eroglu A，Ozdemir G.An Economic Order Quantity Model with Defective Items and Shortages［J］.International Journal of Production Economics，2009，106：544－549.

［5］Chan W.M.，Ibrahim R.N.，Lochert P.B.A new EPQ model：Integrating Lower Pricing，Rework and Reject Situations［J］.Production Planning and Control，2003，14（7）：588－595.

［6］Porteus E.L.Optimal lot Sizing，Process Quality Improvement and Setup Cost Reduction［J］.Operations Research，1986，34（1）：137－144.

［7］Lee H.L.，Rosenblatt M.J.Simultaneous Determination of Production Cycle and Inspection Schedules in a Production Systems［J］.Management Science，1987，33（9）：1125－1136.

［8］Vörös J.Product Balancing Under Conditions of quality Inflation，Cost Pressures and Growth Strategies［J］.European Journal of Operational Research，2002，14（11）：153－166.

［9］Kennedy J.，Eberhart R.Particle Swarm Optimization［J］Proc.of Neural Networks 1995，IEEE International Conference on 1995，l4：1942－1948.