基于ARIMA模型预测我国2012年的货运量
余海燕
(湖北大学 商学院,湖北 武汉430062)
一、国内外研究文献综述
Box&Jenkins(1991)对交通量进行了预测,运用的是ARIMA模型。该方法包括模型的识别、模型估算以及模型检验[1]。Cullinance(1992)利用ARIMA模型预测短期生成货运量,在这之后许多研究者使用ARIMA模型预预测波罗的海货运指数(BFI)[1]。Bashi:Z.& El.Hawary M.E.(2003)提出的一种由多个固定单元组成的动态神经网络模型在交通流量预测方面表现了良好的预测[1]。
韦司滢等(1999)将指数平滑法等其他多种方法应用在三峡移民工程建材配送决策支持系统中[2]。赖一飞等(2000)建立灰色系统预测模型,并对金沙江货类的流量流向及过坝货运量进行分析预测[3]。张存禄(2001)运用GM(1,1)灰色系统预测模型对武汉的物流规模进行了预测,系统分析了影响武汉物流中心发展的各种因素,得出2001-2005年武汉货运量年增长率[4]。
杨荣英等(2001)在讨论移动平均值的基础上,提出了移动平均线方法,并介绍了运用移动平均线进行物流预测的方法[5]。刘劲等(2002)在利用增长率系数法对百色地区港口货运量进行了逐一分析[6]。李海建等(2003)利用二次移动平均线模型对芜湖市物流业发展的规模进行了预测[7]。黄荣富等(2003)在进行指数平滑法预测的基础上进行了物流需求多种方法组合预测[8]。林小平等(2003)利用灰色系统理论,建立了成都双流机场货、邮吞吐量的预测模型。并通过实际数据与预测结果的比较,证明灰色模型对于双流机场货、邮吞吐量的预测具有较高的精度[9]。吴振宁等(2004)利用马尔可夫链对灰色模型进行了改进,并将其应用到物流需求预测中[10]。周茵(2007)针对 GM(1,1)模型对离散度大的数据预测精度差的缺陷,将残差灰色预测模型应用到物流货运量预测中[11]。何国华(2008)利用灰色预测模型对区域物流需求进行了研究[12]。潘英英(2008)运用灰色系统模型,对广西物流中心货运需求量进行了动态预测。另外,还有学者针对灰色预测模型的不足,对其进行了改进,并将其应用到物流需求预测中[13]。
二、实证分析与预测
(一)分析时间序列
根据《新中国60年统计资料汇编》中0146.xls中1949-2008年全国货运量的数据、中华人民共和国国家统计局中2009与2010年月度货运量数据的和得到的2009与2010年的年度数据,建立时间序列模型序列,运用 Eviews6.0软件,根据时间序列的折线图、自相关函数(ACF)图和偏自相关函数(PACF)图,以及ADF单位根,观察其是否存在异方差,其趋势以及识别该序列的平稳性。在此,year表示年份,hyl表示表示货运量(万吨)。
首先,运用eviews6.0,做出年份(1949-2010)与HYL(货运量)的散点图。由图1可知,折线向右上方陡直倾斜,且前后的波动幅度不一致。说明该时间序列存在增长趋势,且又存在异方差。
ADF检验的结果:如图,单位根统计量ADF=3.728789,都大于EVIEWS给出的显著性水平1%-10%的ADF临界值,所以接受原假设,该序列是非平稳的。
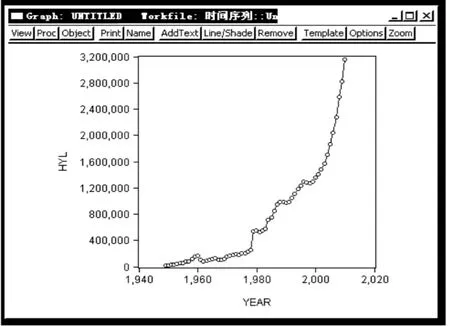
图1 货运量(HYL)的散点图
通过看图,可初步识别序列已平稳。并且ADF的值为-5.105449,分别小于不同检验水平的三个临界值,并且p值接近于零,因此它通过了ADF检验,为一平稳序列。在这里应该注意的是要防止过度差分。一般来说平稳序列差分得到的仍然是平稳序列,但当差分次数过多时存在两个缺点,(1)序列的样本容量减小;(2)方差变大;所以建模过程中要防止差分过度。对于一个序列,差分后若数据的极差变大,说明差分过度。此处,我们认为一阶差分已可以消除序列的非平稳性。
再对hyl进行单位根检验,检验结果如下图2所示。
(二)平稳化处理
从图1和图2得知,该时间序列是非平稳的时间序列,即存在异方差,因此需要对其进行平稳化处理,从而消除异方差。
首先考虑取对数,做出货运量序列的曲线图及ADF检验。发现其仍然呈现非平稳趋势。因此考虑取对数后再进行一阶差分,记为DLhyl。取对数且一阶差分之后的散点图及ADF检验如下所示:
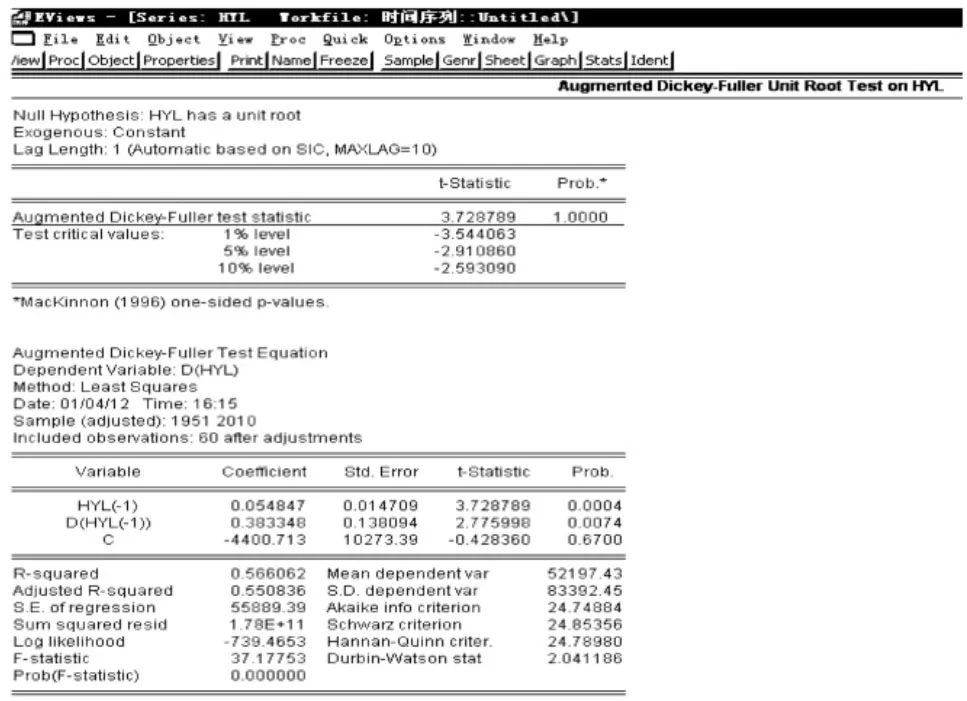
图2 货运量(HYL)的ADF检验
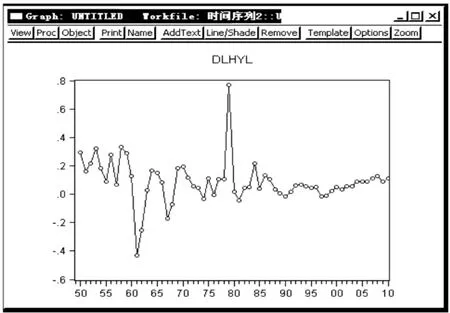
图3 DLhyl的散点图
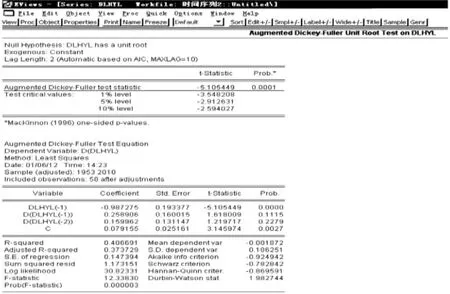
图4 DLhyl的ADF检验图
(三)模型的识别
模型识别即是选择用AR(P)、MA(q),还是用ARIMA(P,q)模型相对平稳的时间序列进行估计。若平稳时间序列的偏相关函数是截尾的,而自相关函数是拖尾的,则可断定此序列适合AR模型;若平稳时间序列的偏相关函数是拖尾的,而自相关函数是截尾的,则可断定此序列适合MA模型;若平稳时间序列的偏相关函数和自相关函数均是拖尾的,则此序列适合ARMA模型。利用Eviews6.0做出一阶对数差分的自相关以及偏相关函数图,以判断模型阶数。从ACF和PACF图可以看出均是拖尾,因此序列适合ARMA模型分析。
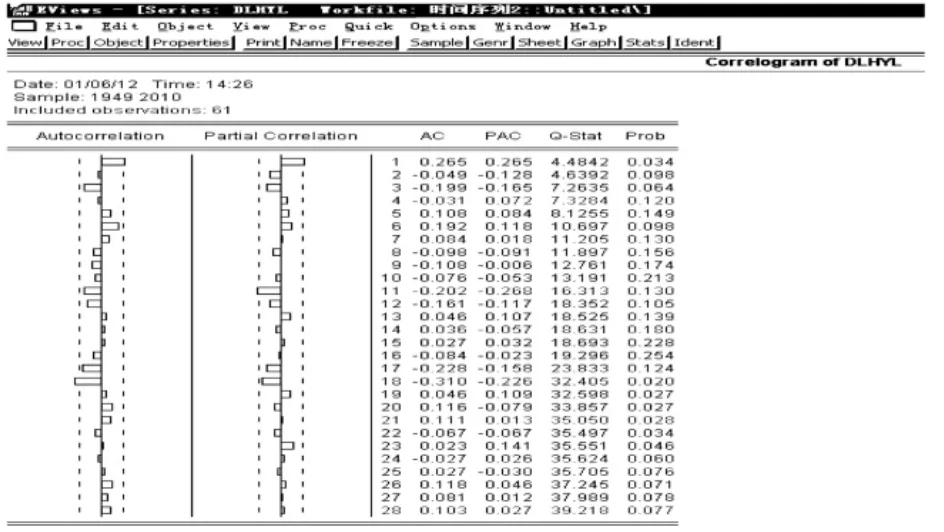
图5 ACF与PACF图
结果如下所示:

图6 回归结果
(四)模型的定阶和参数估计
根据对模型的平稳处理我们已经知道I(d)的阶数为1,即d=1,现在主要对ARMA模型进行定阶分析。经过对图的分析及其运用最佳准则函数定价法,即AIC准则进行反复筛选。最后确定P=2,q=0。即本文中选定ARMA(2,1,0)模型。利用Eviews软件计算输出模型参数,其中LHYLA=LHYL(-1),LHYLB=LHYL(-2),由回归结果可看出R方为0.987939,拟合度很高。P值接近于零,是显著的。
下面是拟合效果图:

图7 拟合效果图
单击Equation窗口中的View→Actual,Fitted,Resid→Table按钮,可以得到拟合直线和残差的有关结果。
由图7的输出结果可以看出,ARIMA(2,1,0)模型的 AIC=-0.9966558,SC=-0.861841。根据 AIC准则和SBC准则,ARIMA(2,1,0)模型可以通过检验。其具体形式如下(根据图7的回归结果可知):

所以,预测2011年的货运量是3303507万吨,2012年的货运量是3405324万吨。
三、结论
运用ARIMA预测法,可得到以下的结果:
第一,2011年的货运量可达到3303507万吨;
第二,2012年的货运量可达到3405324万吨;
第三,由统计数据可知,2010年的货运量为3153400万吨,所以2011年与2010年相比增加了4.76%;
第四,2012年的货运量同2010年相比增加了7.99%;
第五,2012年的货运量同2011年相比增加了3.08%;
由此可知,货运量从长远来看,是成上升的趋势,说明我国物流行业发展速度非常快,西泽修教授是把物流作为“第三利润源泉”,在降低成本、提高效益、增强企业市场竞争力方面起着极其重要的作用,在“十二五”规划中物流最被看好,再一次说明近年内,物流的潜力是非常大的。
[1]陈实.货运量预测方法及应用研究[D].武汉:武汉理工大学硕士论文,2008,12.
[2]韦司滢,张金隆,鲍玉昆.物资配送需求预测的分析[J].物流技术,1999,(3):19-20.
[3]赖一飞,郑清秀,章少强,纪昌明.灰色预测模型在水运货运量预测中的应用[J].武汉水利电力大学学报,2000,(01):96-99.
[4]张存禄,黄培清.武汉地区物流发展水平灰色预测[J].工业技术经济,2001,(05):32-35.
[5]杨荣英,张辉,苗张木.物流预测技术中的移动平均线方法[J].武汉理工大学学报(交通科学与工程版),2001,(03):353-355.
[6]刘劲,谢涛.右江那吉航运枢纽工程货运量分析预测方法[J].广西交通科技,2002,(4):81-83.
[7]李海建,曹卫东,曹有挥.芜湖市物流业发展的现状分析及规模预测[J].安徽师范大学学报(自然科学版),2003,(02):186-190.
[8]黄荣富,陈亚东,潘健.组合预测技术在港口吞吐量预测中的应用研究[J].水运工程,2003,(5):25-27.
[9]林小平,袁捷.基于灰色模型的成都双流机场物流预测[J].武汉理工大学学报(交通科学与工程版),2007,(03):457-459.
[10]吴振宁,黎青松,梁涛,董文龙.基于灰色Markov链配送中心物流量的预测[J].西华大学学报(自然科学版),2004,(S1):123-125.
[11]周茵.残差灰色预测模型在物流需求预测中的应用[J].铁道运输经济,2007,(11):59-61.
[12]何国华.区域物流需求预测及灰色预测模型的应用[J].北京交通大学学报(社会科学版),2008,(01):33-37.
[13]潘英英,宋国喜.基于灰色系统理论的广西物流需求预测模型[J].广西财经学院学报,2008,(01):26-29.

