一类n阶非齐次微分方程初值问题的解
刘琼,黄立壮,李兰
(1.2.广西大学数学与信息科学学院,广西南宁 530004; 3.钦州学院数学与计算机科学学院,广西钦州 535001)
一类n阶非齐次微分方程初值问题的解
刘琼1,黄立壮2,李兰3
(1.2.广西大学数学与信息科学学院,广西南宁 530004; 3.钦州学院数学与计算机科学学院,广西钦州 535001)
关于常系数非齐次微分方程初值问题的显示解,比较常用的是用古典微分方程理论和组合理论,由解的叠加原理,给出初值问题的解法及解的表达式。文中用形式幂级数法,给出了一种n阶非齐次微分方程初值问题的解。
n阶;常系数;非齐次微分方程;形式幂级数;显示解
1 引言
对于常系数非齐次微分方程初值问题的显示解,有着广泛的应用,尤其是在社会、经济领域中有着极其重要的应用,涉及此类问题的解,从理论上寻求更一般的解法很有必要,许多学者在这方面做了大量的工作,也取得了一些重要成果。文献[1]研究了常系数线性齐次常微分方程初值问题的解,根据级数与系数的关系,从麦克劳林级数出发,给出了常系数线性齐次常微分方程解的级数表示,文献[2]探讨幂级数自由项常系数线性微分方程cauchy问题解,得出了cauchy问题一般幂级数解的表达式,但是此类解表达式比较复杂,不容易掌握,文献[3]研究了常系数非齐次微分方程初值问题,利用系数与初始值函数关系,根据叠加原理和比较系数法,得出了常系数非齐次微分方程初值问题显示解的表达式,此类解要求级数在原点范围内一致收敛,避免了按通常解法带来的求解相应高次代数方程的麻烦,为计算机解决有关问题提供了方便,而文献[4]分析了关于常系数非齐次微分方程初值问题的显示解,引入形式幂级数推出了解的表达式,文献[4]相对于文献[1-3]方法比较新,技巧性强,因此本文在文献[4]的基础上结合文献[5]的组合数学知识,给出了一种n阶非齐次微分方程初值问题的解。
2 有关定理
通常对于n阶常系数非齐次微分方程初值问题一般形式:
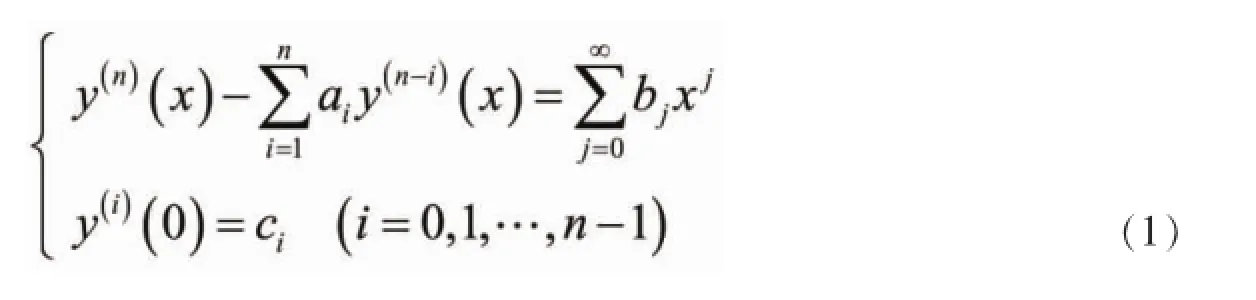
对于这样的非齐次微分方程的初值问题,许多人都进行了探索,方法多种多样,不管是哪种方法都是在特定的条件下,从幂级数的形式寻求求解的可能性,在有些条件下求出的解表达式比较复杂,因此在应用方面价值不大,对于高次微分方程的求解在初始条件给出的情况下,解的表达式与系数有着密切的关系,即使已经给出了解的表达式,绝大多数要想求出解,其过程往往很复杂,所以要求出解,系数的求法很关键,如在求解过程要引入适当变换,从而使求解更简单。
定理2.1
对于下列常系数微分方程初值问题



3 结束语
对于常系数非齐次微分方程初值问题的显示解,很多学者都从不同方面进行了探讨,得出了这方面很多的研究成果,在引言中已经阐述。本文主要是从形式幂级数方面入手,通过引入适当的变换,从而得出了一种简便的阶常系数非齐次微分方程初值问题解的表达式,得出此类解的证明过程往往不是很复杂,比较容易掌握。目的是使解此类问题的过程变得比较简单,能够在实际问题中解答这方面的问题,比较快速得出此类解,减少运算的工作量,提高效率。但是对于这方面更加简便的应用,有待后续研究。
[1]乐茂华.常系数线性齐次常微分方程解的级数表示[J].大学数学,1995,20(2):110-111.
[2]宫子安,余长安.幂级数自由项常系数线性微分方程cauchy问题解[J].松辽学报:自然科学版,1994(1):40-42.
[3]余长安.常系数非齐次微分方程初值问题的显示解[J].武汉大学学报:自然科学版,1997(1):39-43.
[4]刘琼.关于常系数非齐次微分方程初值问题的显示解[J].广西师院学报:自然科学版,1999(2):49-53.
[5]C.L.Liu(美),组合数学导.[M].魏万迪译成都:四川大学出版社,1987.
An Exp licit Solution to Initial Values Problem s for a Class of N-th O rder Non-homogeneous Differential Equation
Liu Qiong1,Huang Lizhuang2,Li Lan3
(1.2.Collegeof Mathematicsand Information Science,GuangxiUniversity,Nanning 530004,Cnina; 3.College of Mathematics and Computer Science,Qinzhou University,Qinzhou 535000,China)
As for the explicit solution to initial values problems for a non-homogeneous differential equation,the traditional differential equation theory and portfolio theory are often applied.In this paper,by themethod of formal power series,the author gives an explicit solution to initial problem of non-homogenous differential equation with constant coefficients.
n-th order;constant coefficient;non-homogeneous differential equation;formal power series;an explicit solution
O175.1
A
1673-8535(2012)06-0050-05
刘琼,湖南益阳人,广西钦州学院数学与计算机科学学院教授,硕士生导师,主要研究方向:微分方程理论及应用。
黄立壮(1984-),男,广西大学硕士研究生,主要研究方向:微分方程理论及应用。
(责任编辑:高坚)
2012-09-12
国家自然科学基金资助项目(10861003),广西自然科学基金项目(0832018z, 0895004-1,0992027-1),钦州学院“专业综合改革试点项目”(钦学院发[2012]119号)
李兰,女,钦州学院2012届数学与应用数学本科学生,研究方向:数学与应用数学。

