波浪对潮流影响的数值模拟及其应用

刘爱珍，王世澎

（1.交通运输部天津水运工程科学研究所水路交通环境保护技术交通行业重点实验室，天津 300456；2.中国石油集团工程技术研究院海洋工程研究所，天津 300451）

波浪对潮流影响的数值模拟及其应用

刘爱珍1，王世澎2

（1.交通运输部天津水运工程科学研究所水路交通环境保护技术交通行业重点实验室，天津 300456；2.中国石油集团工程技术研究院海洋工程研究所，天津 300451）

文章将水动力因素分为潮流特征周期与波浪特征周期两部分，建立了考虑波浪影响的潮流方程。通过考虑波浪引起的辐射应力、表面和底部边界层、Stokes漂流以及Coriolis波浪应力等因素，利用数值方法分析了波浪对潮流场的影响，并将其应用到渤海区域中，分析渤海内波浪对于潮流的影响。

波浪影响；辐射应力；边界层；Stokes漂流；Coriolis波浪应力

Biography：LIU Ai-zhen（1979-），female，engineer.

海岸河口地区长期的、主要的水动力因素是波浪和潮流，是其他各种物质输运诸如污染物的对流扩散、泥沙输运等的动力学基础。波浪与潮流，无论在时间尺度或空间尺度，都存在很大的差别，因此现阶段对于波流相互作用的研究，主要采用2种不同的概化方法：第一种方法是把周期变化的潮流概化成具有某一特征的海流，叠加到波浪运动方程中去，用来模拟波流运动结构在短时间内所发生的变化。对于波浪来说，海流的作用既有运动学影响又有动力学的影响。在运动学方面，包括水深和海流对波浪频散关系的影响。另外还有由于顺流或逆流引起的波长的变化；在动力学方面，海流将引起波浪波高的变化［1］；另一种方法则是把波浪过程概化为在潮周期中具有平均意义的波浪要素，叠加到潮流运动方程中，用来计算波浪对流的运动状态的影响，主要着眼于波浪和潮流对于泥沙的输运研究［2］。

波浪对潮流的影响主要可以归结为以下几个方面：首先是波浪产生的辐射应力，是波浪对潮流作用的一个十分重要的物理量。波浪辐射应力又称为剩余动量流，是Longuet-Higgins和Stewart［3］提出的概念，在牛顿流体力学定理和速度沿水深均匀分布的基础上，将波浪辐射应力张量定义为由于波浪现象产生的动量超通量。由于波浪的存在，对潮流作用一个明显的特征就是波浪表面与底部边界层的存在。Longuet-Higgins［4］在考虑粘性的非地转坐标系统下证明：在波浪场水面和水底存在2个极薄粘性边界层，会严重影响波浪下方水体的输运过程，而且无论粘性小到何种程度，都将如此。上述影响相当于在水表面存在一个虚拟的切应力，而同时在水底存在一个稳定的流动。边界层理论和试验的一些工作表明，由于高频表面波的存在，低频流动的底部边界层会有明显的变化［5］。对于非线性波浪，波浪对于潮流的影响，其中一方面体现为Stokes漂流，Stokes漂流是由水波的非线性效应诱生的一种平均流动［6］。当Stokes漂流与Coriolis力共同作用时，会产生附加的波浪应力，是旋转系统中的一个特殊的现象，Pollard［7］通过分析得出，当波浪平行于波峰方向的速度分量与波浪速度的垂直分量同相位时，波浪平均的雷诺应力会增加，其中增量定义为柯氏波浪应力。

文中根据流体的水动力学特征，将流体物理量分为潮流特征周期与波浪特征周期部分，在波浪周期内进行平均，建立考虑波浪影响的潮流方程，利用数值方法模拟考虑波浪影响的潮流特性，探讨波浪影响特征。

1 数学模型的建立

1.1 基本方程

从海域中的水体动力学特性来看，流体物理量可视为长周期运动部分和短周期部分

式中：字母大写，表示长周期运动物理量；字母小写，并且带角标w的为短周期运动物理量。对式（1）各量取波周期平均后

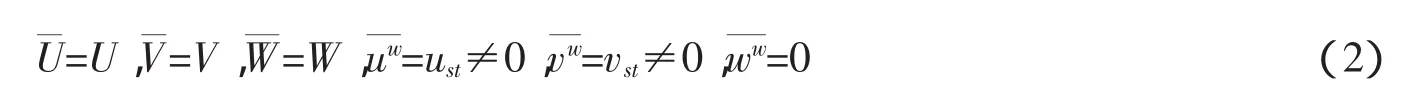
将式（1）～式（2）代入到流体控制方程中，在波浪周期内平均，可得到考虑波浪影响的潮流方程，在σ坐标下可以表示为

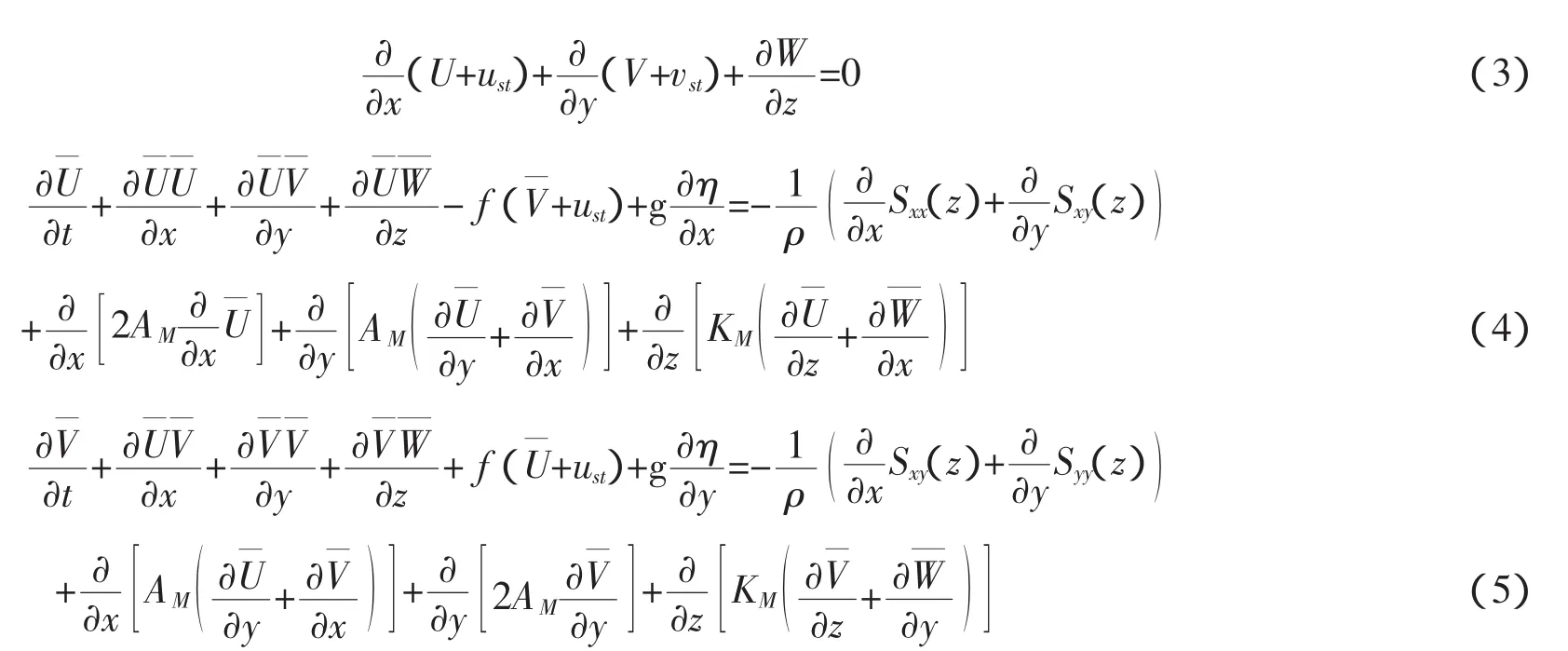
式中：U，V 为水平方向的流速；H=D+η，为总水深，D 为静水深，η 为潮位。Sxx，Sxy，Syy为三维波浪辐射应力。Xia［8］在波浪周期平均后，将辐射应力在垂向上不再积分，计算到平均水平面。从而得到辐射应力的垂向分布，通过积分整理后可得

1.2 边界条件

考虑波浪影响的自由表面边界条件

底部边界条件

波流共同作用下的底应力需要迭代求解［9］。

1.3 数值求解

本文采用等间距网格的差分方法求解，利用ADI（Alternating Direction Implicit）法，在矩形域中，分别在x方向和y方向进行求解，使问题转化为求解2个三对角矩阵，具体的离散方程不再叙述。

2 渤海应用

渤海潮流场的计算范围包括了整个渤海（图1）。模型的开边界定在远离研究区域的122°经线上，边界水位由南北2个验潮站大连和烟台的调和常数（M2、S2、K1、O1）计算后插值得到，计算网格取为1 000 m×1 000 m，总计算网格数为 390×480，面积约 187 200 km2，模型选取的时间步长为180 s。

渤海潮流计算结果与渤海沿岸10个验潮站位的分潮振幅与迟角进行了比较，计算值与实测结果均基本吻合，比较结果见表1，可以看出绝大部分计算结果与实测结果接近。可见该模型所模拟的潮流运动基本能够反映出渤海海域的水流状况，可以作为进一步分析计算的基础资料。此模型在蓬莱港、天津港、营口港等海区的潮流计算中也得到了较好的验证［10-12］。图2、图3分别为渤海涨落急时刻潮流场图。

利用已验证的数学模型，计算渤海海域内5 d的潮流过程，在第3 d开始，添加波浪的影响，模拟3 d考虑波浪影响的潮流。通过对渤海海域风资料的分析，常见风向为SW向。因此在这里，假设存在一定常的SW向风场，风速设计为12 m/s，6级风。

图1 渤海模型计算范围及验证点位置Fig.1 Computed area and observed position of tidal current in Bohai Sea

图2 涨急时刻渤海潮流场Fig.2 Tidal current field at flood strength of tide in Bohai Sea

图3 落急时刻渤海潮流场Fig.3 Tidal current field at ebb strength of tide in Bohai Sea

在计算域内选取5个点进行比较，对比点位置见图4。图5为潮位影响过程，图6为潮流影响过程。通过计算结果来看，选取的对比点潮位受到影响很小，可以说波浪对于潮位的影响很小，几乎可以忽略。对于潮流而言，在不同水深情况下，波浪的影响使得潮流垂向结构产生变化。从对比点计算结果来看，波浪对于潮流垂向平均流速影响较小。在这里选取2个特征时刻的流速垂向结果来分析波浪影响。

辽东湾内，波浪较小，对于潮流影响较小。从点A（水深约2 m）的计算结果来看，波浪的影响使得潮流流速2个方向上的分量产生不同的变化，但是垂向平均后的流速并没有较大的变化。从其计算结果来看，波浪影响的量级在10-2～10-1。

对于渤海湾，地形变化较缓，在渤海湾湾顶水深很浅，有较大面积的浅滩。湾内的波浪情况与辽东湾内的类似。点D（水深约15m）位于渤海湾内，潮流流速主要呈水平向。波浪的影响主要体现在水体上部，潮流流速变化较大。随着深度的增加，波浪影响逐渐减弱，对于2个方向的流速产生不同的影响。从2个方向的流速对比结果来看，波浪影响的量级在10-1左右。

波浪在莱州湾内变化较大，波浪对潮流的影响主要表现在水体上部，使得2个方向产生相反的变化，其中一个方向的流速增大，另外一个方向的流速减小。由于C点水深在10 m左右，总的波浪影响产生的量级在10-2左右。

渤海中部与渤海海峡的水深较深，风浪较大，对于潮流流场产生的影响较大，点B、点E的水深均在20 m左右，从其计算结果来看，波浪的影响使得水体上部流速产生较大的变化，随着深度的增加，影响逐渐减弱。在渤海海峡内，波浪较大，使得水体上部流速变化较大。从设计工况中的计算结果来看，波浪影响的量级在10-2～10-1。

表1 渤海潮汐观测站各分潮调和常数与计算结果比较Tab.1 Simulated and observed tide harmonic constant

图4 渤海内对比点位置Fig.4 Compared points positions in Bohai Sea

图5 A～E点潮位过程Fig.5 Tidal elevation time series in point A～E

图6 A～E点垂向平均流速过程Fig.6 Tidal current depth-averaged time series in point A～E

3 结论

从计算的结果来看，在渤海不同的区域内，波浪会对潮流产生不同的影响，尤其是在潮流垂向结构上，但是对于潮位和垂向平均流速过程影响很小，不会影响整个渤海海域内各分潮的振幅分布。在深水情况下，波浪的影响使得潮流垂向结构重新分布，但是对垂向平均流速以及潮位过程影响很小。随着水深的变浅，波浪影响使得水体上部的流速产生变化。在浅水区域，波浪的影响对潮流流速在2个方向上的分量产生不同的变化，但是垂向平均后的流速变化很小。从计算结果来看，整个渤海海域内波浪影响的量级在10-2～10-1。

［1］LI Y C.Wave-current interaction［M］.Houston：Gulf Pub Co.，1990：703-726.

［2］孙文心，江文胜，李磊.近岸环境流体动力学数值模拟［M］.北京：科学出版社，2004.

［3］Longuet-Higgins M S，Stewart R W.Radiation stress in water waves：a physical discussion with application［J］.Deep Sea Research，1964，11：529-562.

［4］Longuet-Higgins M S.Mass transport in water waves［J］.Philos.Trans.Roy Soc.，1953，245：535-581.

［5］Grant W D，Madsen O S.The continental-shelf bottom boundary layer［J］.Annual Reviews of Fluid Mechanical，1986，18：265-305.

［6］文圣常，余宙文.海浪理论与计算原理［M］.北京：科学出版社，1984.

［7］Pollard R T.Surface waves with rotation：an exact solution［J］.Journal of Geophysical Research，1970，75：5 895-5 898.

［8］XIA H Y，XIA Z W，ZHU L S.Vertical variation in radiation stress and wave-induced current［J］.Coastal Engineering，2004，51（4）：309-321.

［9］ Signell R P，Beardsley R C，Graber H C.Effect of wave-current interaction on wind-driven circulation in narrow，shallow embayment［J］.Journal of geophysical research，1990，95（6）：9 671-9 678.

［10］周斌，王连湘，刘爱珍，等.蓬莱港通用码头环境影响报告书［R］.天津：交通部天津水运工程科学研究所，2006.

［11］李欣，刘爱珍.辽宁龙德船业海洋环境影响报告书［R］.天津：交通部天津水运工程科学研究所，2006.

［12］张光玉，李亚娟，刘爱珍，等.天津港总体规划环境影响报告书［R］.天津：交通部天津水运工程科学研究所，2006.

Effect of wave on tidal current and its application

LIU Ai-zhen1，WANG Shi-peng2
（1.Tianjin Research Institute for Water Transport Engineering，Key Laboratory of Environmental Protection Technology on Water Transport Engineering，Ministry of Transport，Tianjin300456，China；2.Research Institute of Engineering Technology，CNPC，Tianjin300451，China）

The hydrodynamic factors were divided into two part cycles of characteristics of tidal current and wave characteristics in this paper，and the flow equation was established by considering the wave influence.By considering the wave-induced radiation stress，surface and bottom boundary layer，as well as Coriolis Stokes drift wave stress，the effect of wave on flow field was analyzed by numerical method，which was applied to the analysis of wave effect in the Bohai Sea region.

wave effect；radiation stress；boundary layer；Stokes drift；Coriolis wave stress

TV 139.2；O 242.1

A

1005-8443（2012）03-0212-07

2011-06-20；

2012-01-19

刘爱珍（1979-），女，山东省东营市人，工程师，主要从事海洋动力学研究工作。