5Cr-0.5Mo耐热钢寿命预测中主曲线非参数统计分析

李建东

（太原理工大学 数学学院，太原030024）

随着石油、化工、电力及航空航天等领域的发展，高温材料持久寿命预测技术在高温构件设计和延寿评估中的重要作用日益显现。它既有助于高温构件检修时间间隔的准确制定，又能最大限度地提高资源利用率，具有重要的经济和社会意义。

目前，寿命预测技术的发展已经历了四个阶段：最早采用的是线性外推［1］，侧重研究蠕变过程的断裂机理；第二阶段是蠕变损伤法［2］，侧重研究材料组织变化；第三阶段是参数外推［3－4］，如 Larson-Miller参 数、Manson-Haferd 参 数、Orr-Sherby-Dorn 参数、Manson-Succop参数等，其中 Larson-Miller参数在工程上应用最为广泛；第四阶段是外推中的解析法，是第三阶段的进一步丰富和发展，如θ法寿命评估［5－6］。从统计角度出发，第三阶段的参数外推中Time-Temperature-Parameter（TTP）方法在实际中应用较多。寿命预测技术在TTP参数的基础上，也得到相应的研究和发展。传统上利用TTP参数对蠕变数据进行压缩，建立对数应力与TTP参数的主曲线，拟合方法多采用多项式拟合［6］；但赵杰等［7］研究表明，多项式拟合在已有数据带内能得到很好的预测效果，但预测条件超出已有的数据带时，由于多项式曲线的变化而导致推算结果有较大的误差。在此基础上，李东明［8］提出一种主曲线（单指数形式），在一定程度上避免了因外推而产生的较大偏差。传统方法中无论TTP参数的建立，还是主曲线的拟合，都是建立在一定假设的基础上，均有一定的局限性。

伴随计算机运算能力的增强，非参数统计在近一、二十年得到快速的发展，像非参数回归、小波分析等非参数统计方法应运而生。非参数回归可以在对总体不进行任何假设情况下，对总体进行回归推断，所建模型具有较强的稳健性。然而至今对5Cr－0.5Mo耐热钢进行的非参数统计分析的研究还不多。

本文利用所收集的日本材料金属研究所在1992年发布的238个5Cr-0.5Mo耐热钢的蠕变数据［9］（σ，tr，T）（σ为应力，tr为蠕变断裂寿命，T 为温度），对5Cr-0.5Mo耐热钢寿命预测中占有重要地位的主曲线进行非参数统计分析。利用局部线性回归方法，提出新的主曲线形式，并得到5Cr-0.5Mo耐热钢双指数形式主曲线具体表达式。

1 主曲线非参数统计方法的处理分析

参数外推法首先用TTP参数（本文选用李东明［8］推荐的Larson-Miller参数）对蠕变数据压缩，然后得到应力对数与P参数的散点图。可是进行主曲线拟合时，传统上不管是用多项式拟合，复合形式拟合还是其他已知函数形式拟合，都具有一定假设。而非参数统计方法不需要任何假设就可以对数据进行拟合。在非参数回归方法中有局部线性回归、核回归、局部多项式回归，其中局部线性回归在不增加方差的条件下减少设计偏倚和边界偏倚，避免了边界点拟合精度不高的不足，而且有完善的理论基础，故本文利用局部线性回归对5Cr-0.5Mo耐热钢主曲线进行处理。

2 结果和讨论

赵杰［7］的研究表明主曲线多项式拟合存在不足。李东明［8］提出了单指数形式主曲线并得出较好的预测结果。因此本文所得主曲线的拟合效果仅与单指数主曲线的拟合结果比较。

2.1 主曲线的拟合

选用李东明［8］推荐的Larson-Miller参数P＝10－3T（lgtr＋17），利用R统计软件编程，选用使广义交叉验证（GCV）最小的条件下的带宽h，并利用局部线性回归得出新的主曲线。

主曲线形式（双指数）：

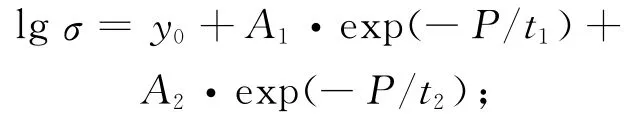
回归系数：

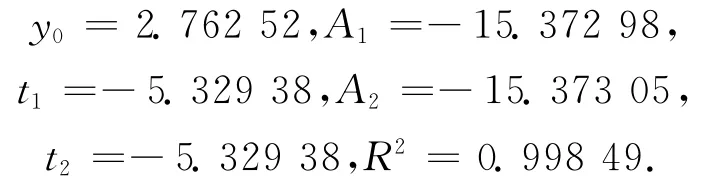
而利用李东明［8］提出的主曲线形式拟合得出的结果如下。

主曲线形式（单指数）为

lgσ＝a＋b·P＋c·exp（d·P）；

回归系数为

a＝3.128 68，b＝0，c＝－0.067 109，

d＝0.167 175，R2＝0.979 42.

这里

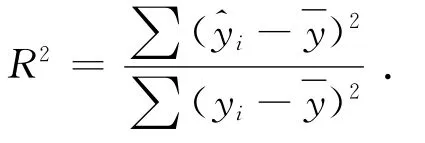
R2为拟合主曲线的决定系数，它体现拟合得到的主曲线符合原数据点分布趋势的程度，其中yi为lgσ，主曲线越能更合理地表征数据点的分布趋势。

由5Cr-0.5Mo耐热钢全部蠕变断裂数据拟合后的双指数形式与单指数形式主曲线分别如图1和图2所示。

由拟合两种主曲线方程的决定系数R2的值可定量地确定局部线性回归得到的双指数主曲线比单指数主曲线有较高的拟合度，说明本文的双指数主曲线方程能更好地表征数据点的分布趋势。这一点通过图1与图2的比较也可以看出，双指数主曲线无论是在数据带边界或中间都更好地穿过数据带的中部，也符合经验下主曲线随着参数P的增大越向下弯曲的趋势，即拟合得更好。

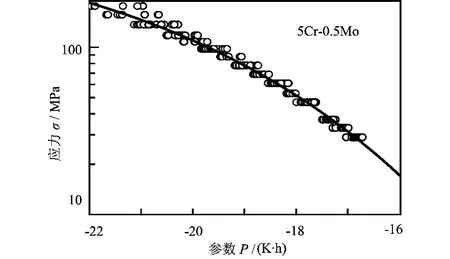
图1 双指数主曲线

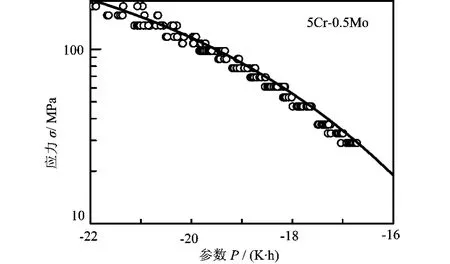
图2 单指数主曲线

2.2 双指数主曲线的推断精度检验

实际数据是最能检验模型合理性的武器。高温材料的蠕变断裂数据的获取少则几年，多则几十年，需要花费大量的人力，物力和财力，得之不易。为了能用实际数据来检验模型所得的主曲线的稳健性及其外推精度，本文将5Cr-0.5Mo耐热钢的238个蠕变数据以蠕变断裂时间半年（约4 300h）为界，分成短时蠕变断裂（117个）数据与长时蠕变断裂数据（121个）两组。利用本文的方法用117个短时蠕变数据来获得主曲线，用121个长时蠕变数据来检验由117个短时数据拟合所得的双指数主曲线的稳健性及其推断情况。

由局部线性回归对短时数据拟合得到的双指数主曲线如图3所示。

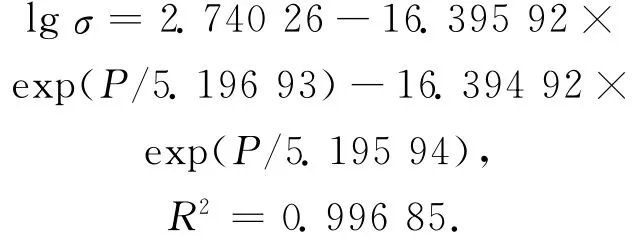
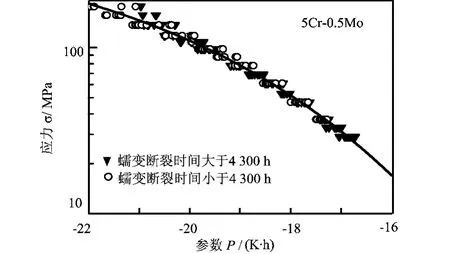
图3 由断裂时间小于4 300h的数据拟合的双指数主曲线

由图3可以看出，由短时蠕变断裂数据所得双指数主曲线能很好地穿过长时蠕变断裂数据和全部数据带的中部，这说明利用本文方法可以仅利用5Cr-0.5Mo耐热钢短时数据建立主曲线，得出lgσ与P的关系，建立σ，tr，T三者之间的关系，从而确定在较低温度T或较低应力σ下的较长蠕变断裂时间tr，实现了蠕变断裂寿命tr外推和预测。本文也在图4中同时描绘出由5Cr-0.5Mo耐热钢的短时数据所拟合的主曲线及其全部数据点所拟合主曲线，发现二者几乎重合，这表明对于该耐热钢寿命的预测可以仅通过在高温或高压下得到的短时数据就可以对低温或者低压下的长时蠕变断裂寿命tr进行推断，不需要过多的长时蠕变断裂数据，从而节省了耐热钢寿命预测中因获得大量长时数据而造成的成本。检验结果显示，利用本文方法所得5Cr－0.5Mo耐热钢的主曲线具有较好稳健性和统计推断特性，从而本文方法和结论为该材料由短时蠕变断裂数据推断长时数据提供了有力依据，为该材料下一步的寿命预测和可靠性分析提供了理论平台。

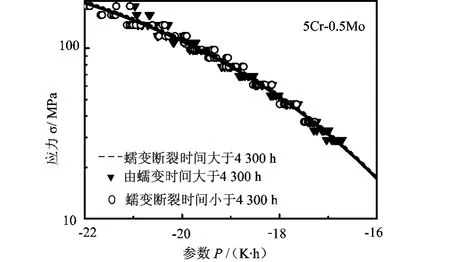
图4 由短时数据和全部数据拟合的双指数主曲线

［1］ Klok J.Residual Life Assessment［M］.Germany：Mannheim，1992.

［2］ Mukhopauhyay N K，Chowdhury S G.Remaining life estimation of a service exposed economiser tube［J］.Engineering Failure Analysis，1999，6（4）：233-243.

［3］ Kouichi M，Hideaki K.Prediction of long term creep curve and rupture life of 2.25Cr-1Mo steel［J］.ISIJ International，1990，30（10）：817-832.

［4］ Ray A K，Tiwari Y N.Residual life prediction of service exposed main steam pipe of boilers in a thermal power plant［J］.Engineering Failure Analysis，2000（7）：359-376.

［5］ Evans R W，Wilshire B.Creep of Metals and Aollys［M］.London：The Institute of Metals，1985.

［6］ Zhao Jie，et al.Introduction of SCRI model for creep rupture life assessment［J］.Pressure Vessels and Piping，2009，86：599-603.

［7］ Zhao J，Han S Q，Gao H B，et al.Remaining life assessment of a CrMoV steel using the Z-parameter method［J］.Int J Pressure Vessels Piping，2004，81：758.

［8］ Li D M.Statistical Analysis on Creep Rupture Property of Heat Resistant Steel［D］.Dalian：Dalian University of Technology，2006.

［9］ National Researeh Institute for Metals.NRIM Creep Data Sheet No.12B［R］.Tokyo：Sanko Kabushiki Kaisya，1990.